Referencia: Lathi 1.3.2 pdf/p.63, Estándar ISO16, Frecuencias de afinación de un piano
Señal determinística, conocida como una señal cuya descripción física es completamente conocida por su forma matemática o gráfica.
Ejemplo: Señal 440 Hz
Es una señal que puede ser escrita de forma determinística como:
x(t)= cos(2\pi f t)Siendo f=440 Hz
La señal de 440 Hz es usada como la frecuencia referencia para la afinación de todos los instrumentos musicales desde 1936, adoptada por ISO en 1955 y reafirmado en 1975 como ISO16.
Algoritmo en Python – Graficar en dominio del tiempo
El audio del archivo.wav se puede escuchar con windows media player. Para visualizar la forma de señal del archivo.wav, se puede usar python para leer el archivo y graficar la señal en el dominio del tiempo.
El archivo.wav debe encontrarse en el mismo directorio que el archivo .py de python.
# Señales analógicas import numpy as np import matplotlib.pyplot as plt import scipy.io.wavfile as waves # INGRESO # archivo = input('archivo.wav a leer: ') archivo = '440Hz_44100Hz_16bit_05sec.wav' [muestreo, sonido] = waves.read(archivo) # SALIDA - Observación intermedia print('frecuencia de muestreo: ', muestreo) print('dimensiones de matriz: ', np.shape(sonido))
frecuencia de muestreo: 44100 dimensiones de matriz: (220500,)
Nota: si el archivo.wav tiene etiquetas, se descartan para el ejercicio. por lo que se presenta una advertencia «WavFileWarning».
c:\python34\lib\site-packages\scipy\io\wavfile.py:179: WavFileWarning: Chunk (non-data) not understood, skipping it. WavFileWarning)
Existen 220500 muestras en el archivo del ejemplo, que en una sola gráfica puede resultar muy denso y poco observable. La gráfica se limitará a una ventana de tiempo del archivo definida en el rango de tiempo por inicio y termina, con valores en el rango de milisegundos.
El rango de la ventana puede cambiarse si es de interés usar otro rango de tiempo.
De las dimensiones de la matriz (220500,), se determina que el audio es de tipo monofónico al tener una sola dimensión. El audio estéreo tiene dimensiones de (n,2).
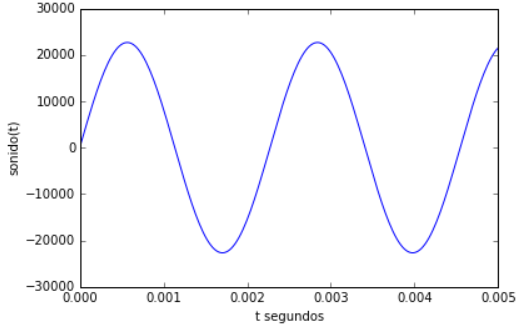
# PROCEDIMIENTO # ventana de observación inicia = 0 termina = 0.005 canal = 0 # selecciona datos dt = 1/muestreo t = np.arange(inicia,termina,dt) muestras = len(t) fragmento = sonido[int(inicia/dt):int(inicia/dt)+muestras] # SALIDA plt.plot(t,fragmento) plt.ylabel('sonido(t)') plt.xlabel('t segundos') plt.show()

Aunque la señal es simple de ver, y oir, la riqueza del sonido de un instrumento corresponde a otros componentes de frecuencia que los hace únicos al oido estando en la misma nota musical.
