ESTG1003 – FCNM – ESPOL
3ra Evaluación II Término 2017-2018. Febrero 20, 2018
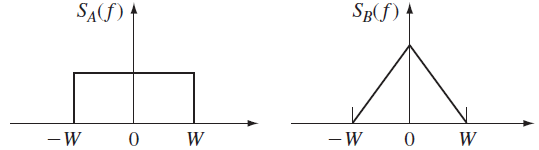
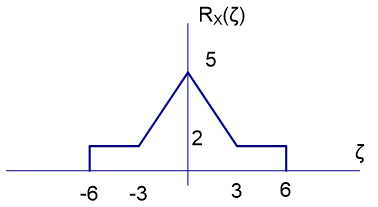
Tema 4. (25 puntos) La señal de entrada X(t) de un sistema tipo “QAM” son procesos aleatorios A(t) y B(t) independientes con densidades espectrales de potencia mostradas.
X(t) = A(t) cos(2πfct + θ) + B(t) sin(2πfct + θ)
a) Encuentre la densidad espectral de potencia de la señal QAM, SX(f)
b) Grafique su respuesta
Rúbrica: literal a (15 puntos), literal b (10 puntos)
Tema 2 (50 puntos). Sea X(τ) un proceso estocástico normal y estacionario de media 1 y autocorrelación:
R_X (\tau)=\frac{18}{9 + \tau^2} + 1
\tau \in \Re
a) Calcular la P(|X(3)|>1)
b)Determinar la matriz de covarianzas de la variable aleatoria tridimensional [X(0),X(1),X(3)]
c) La autocorrelación del proceso estocástico
Y(t)=2X(t+2)+t
d) La función de densidad de la variable aleatoria
Z=X^2 (3)
d) SX(f) y Graficarla
Rúbrica: cada literal (10 puntos)
Tema 4 (25 puntos). Sea X(t) un proceso estocastico estacionario en el sentido amplio (WSS) con valor esperado E[X(t)]=a y con una SX(f).
Considere la variable aleatoria Θ con distribución uniforme en (0, 2π) que es independiente de la variable aleatoria definida X(t), y el proceso :
Y(t) = 2 X(t) cos (\omega_0 t + \Theta)a) Determine si el proceso Y(t) es WSS
b) Encuentre SY(f) y SX(f).
Tema 3 (30 puntos). Dada la siguiente función de Autocorrelación Rx(ζ) del proceso estocástico X(t) que es WSS.
a) (15 puntos) Encuentre Var[X(t)]
b) (15 puntos) Sx(w) ( o Sx(f))
Transformadas de Fourier
x(t) \rightarrow X(\omega) g(t) \rightarrow \int_{-\infty}^{\infty} g(t) e^{-j2 \pi ft} dt rect\left( \frac{t}{\tau}\right) \rightarrow \tau sinc\left( \frac{\omega \tau}{2}\right) tri\left( \frac{t}{\tau}\right) \rightarrow \frac{\tau}{2} sinc^2(\frac{\omega \tau}{4})Tema 3 (30 puntos). Un proceso aleatorio estacionario en sentido amplio X(t) con densidad espectral de potencia:
\Im_{XX}(\omega) = 50 \pi \delta(\omega) + \frac{3}{1+\left(\frac{\omega}{2}\right)^2}se aplica a una red con respuesta impulso
h(t) = 2 e^{-2t} \mu (t)obteniendo luego de la red Y(t)
Determine:
a) Var[X(t)]
b) La densidad espectral de potencia de la respuesta de Y(t)
c) La potencia de Y(t)
Pares de Transformadas de Fourier:
x(t) \leftrightarrow X(\omega) 1 \leftrightarrow 2 \pi \delta(\omega) e^{-at}\mu (t) \leftrightarrow \frac{1}{a+j\omega} te^{-at}\mu (t) \leftrightarrow \frac{1}{(a+j\omega)^{2}} t^{n}e^{-at}\mu (t) \leftrightarrow \frac{n!}{(a+j\omega)^{n+1}} a>0Tema 1 (30 puntos). Asuma un proceso estocástico estacionario en el sentido amplio X(t) con función de autocorrelación
R_X(t) = e^{-|t|} t \in \Rea) Determine la densidad espectral de potencia del proceso
A(t) = X(t) - X(t-1)Si se define el proceso estocástico
B(t) = X(t) cos(t+ \rho)donde ρ es una variable aleatoria independiente de X(t) con distribución uniforme en el intervalo (0, π), determine:
b) Es B(t) estacionario en el sentido amplio
c) La mínima diferencia de tiempos para la cual dos variables aleatorias de B(t) son independientes entre sí.
Indicación: 2 cos(a) cos(b) = cos(a + b) + cos(a − b)