Referencia: Leon-García p.97, Gubner p.64
Variables Aleatorias
Una variable aleatoria se define como una función que asigna un valor numérico real X(ω) a cada resultado del experimento en un espacio muestral.
Una función es una regla para asignar un valor numérico a cada elemento de un grupo.
La espacio muestral S es el dominio de la variable aleatoria
Ejemplo
León-García 3.1., Gubner 2.1,
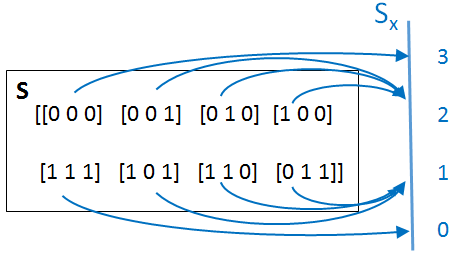
Una moneda se lanza tres veces y se anota la secuencia de caras (0) o sello(1). El espacio muestral para el experimento es
S={000, 001, 010, 011, 100, 101,110, 111}
Sea X el número de caras en tres lanzamientos, X asigna a cada resultado ω en S un número del grupo SX={0,1,2,3}.
Encuentre los valores para X(ω)
# número de caras en lanzamiento de monedas import numpy as np import itertools as iter # INGRESO posibles = 2 lanzamientos = 3 # PROCEDIMIENTO moneda = np.arange(posibles) n = posibles**lanzamientos # Espacio muestral de lanzamientos resultados = list(iter.product(moneda, repeat=lanzamientos)) S = np.asarray(resultados) # SALIDA - Observación intermedia print (S)
[[0 0 0] [0 0 1] [0 1 0] [0 1 1] [1 0 0] [1 0 1] [1 1 0] [1 1 1]]
# número de caras en cada lanzamiento cuenta = [] for experimento in S: caras = lanzamientos - np.sum(experimento) cuenta.append(caras) Sx = np.unique(cuenta) # SALIDA - Observación intermedia print('Sx: ',Sx) print('evento, X(evento)') for i in range(0,n): print(S[i],cuenta[i])
Sx: [0 1 2 3] evento, X(evento) [0 0 0] 3 [0 0 1] 2 [0 1 0] 2 [0 1 1] 1 [1 0 0] 2 [1 0 1] 1 [1 1 0] 1 [1 1 1] 0
Ejemplo
León-García 3.2. Apuestas
Un jugador paga $1.50 para poder participar en un juego: Se lanza una moneda tres veces y se cuenta el número de caras X. El jugador recibe $1 si X=2 y $8 si X=3, $0 en los otros casos.
Sea Y el premio del jugador, Y es una función de la variable X con resultados relacionados con el espacio muestral del experimento aleatorio (juego)
Y = np.zeros(n, dtype=float) for i in range(0,n): if (cuenta[i]==2): Y[i]=1 if (cuenta[i]==3): Y[i]=8 Sy = np.unique(Y) # SALIDA print('Sy: ',Sy) print('evento, X, Y') for i in range(0,n): print(S[i],cuenta[i],Y[i])
Sy: [ 0. 1. 8.] evento, X, Y [0 0 0] 3 8.0 [0 0 1] 2 1.0 [0 1 0] 2 1.0 [0 1 1] 1 0.0 [1 0 0] 2 1.0 [1 0 1] 1 0.0 [1 1 0] 1 0.0 [1 1 1] 0 0.0
Una función de una variable aleatoria, produce otra variable aleatoria.
Ejemplo
León-García 3.3. Apuestas lanzando una moneda
Sea X el número de caras en lel lanzamiento de una moneda.
Encuentre la probabilidad del evento {X=2}.
Encuentre la probabilidad que el jugador gane $8 en el ejemplo anterior.
X(ω)=2 si ω esta en {000,010,001}, por lo que:
P[X=2] = P[{000,010,001}] = P[{000}] + P[{010}] + P[{001}] = 3/8
El evento {Y=8} ocurre solo con el resultado cuando ω = [000], por lo que:
P[Y=8] = P[{000}] = 1/8