A.I. U1 Introducción a la Automatización Industrial
1.- Introducción a los sistemas de control
1.1 Conceptos
1.2 Simbología
1.3 Sistemas de control en lazo abierto.
1.4 Sistemas de control en lazo cerrado.
1.5 Tipos de control de sistemas

1.1 Conceptos
De acuerdo al panorama histórico en la ingeniería de Control data desde el siglo XVII, con el trabajo de James Watt para el control de velocidad de una máquina de vapor, Minorsky en 1922, Nyquist en 1932 y Hazen en 1934, entre otros, proporcionaron importantes aportes para el desarrollo de la teoría de control.
Se puede destacar principalmente que la ingeniería de control, consiste en el desarrollo de las siguientes etapas:
- Modelamiento de la planta.
- Análisis de estabilidad y comportamiento dinámico.
- Análisis y propuesta de control.
- Diseño, sintonización y simulación del controlador.
- Implementación y verificación del funcionamiento (pruebas correspondientes).
La Teoría de Sistemas de Control Automático, es una temática que aborda el aprendizaje de las técnicas de modelamiento de sistemas físicos, y el conocimiento de herramientas matemáticas e informáticas, que permitan el análisis y el uso de estrategias de diseño de sistemas de control.
Su implementación permitirá garantizar el adecuado funcionamiento de la planta o sistema controlado.
Es importante enfatizar sobre algunos conceptos manejados en la teoría de control, tales como:
Señal: Cantidad física que se desarrolla a través del tiempo y posee información de interés.
Sistema: Integración de elementos de distinta naturaleza, que permiten generar o modificar señales
Control: Dominio, manejo, comando, gobierno o regulación de un sistema.
Teoría del Control Clásico.
Comprende un análisis de sistemas de control, usando la herramienta matemática de Laplace y su comportamiento en el plano de la variable compleja (s). El modelado de la planta se presenta mediante una Función de Transferencia G (s), la misma que es definida posteriormente. Uno de los alcances relevantes en este campo, es el controlador de tres términos PID (Proporcional, Integrador, Derivador). El uso de la matemática de la transformada de Laplace, para la solución de las ecuaciones diferenciales que gobiernan el sistema, presenta las siguientes ventajas:
1.Permite modelar y resolver sistemas que poseen componentes de diferente naturaleza, como por ejemplo componentes eléctricos, mecánicos, térmicos, entre otros, que al interactuar entre sí constituyen un solo mecanismo.
2.Facilita la solución de las ecuaciones diferenciales, al convertir estas ecuaciones en un caso de solución de ecuaciones algebraicas de menor complejidad, al estar representadas en el dominio de la variable compleja (s).
3.Permite obtener la solución de las ecuaciones diferenciales en forma directa, lo cual reemplaza el procedimiento clásico de emplear un tratamiento independiente para obtener una solución homogénea y una solución particular.
4.Permite simplificar bloques de función de transferencia que se encuentran en cascada, tan solo con realizar el producto de las funciones de transferencia de los mismos, evitando la complejidad, de realizar el proceso correspondiente que es la operación de convolución, para cuando los bloques estén representados como modelos en función del tiempo.
Teoría de Control Moderno.
Se caracteriza por estar sustentado principalmente en un análisis temporal, mediante el planteamiento de ecuaciones diferenciales y herramientas matriciales. El modelado del sistema está constituido por un conjunto de ecuaciones diferenciales de primer orden, cuyas variables se conocen como variables de estado y representan los estados del sistema, de esta manera el modelo toma su nombre de modelo en espacios de estados. La representación matemática en forma generalizada de acuerdo alas ecuaciones:
x ̇ = Ax + Bu
y = Cx + Du
x ̇ - Matriz de estados derivados.
x - Matriz de estados.
u - Matriz de entradas del sistema.
A - Matriz de Transición (característica del sistema).
B - Matriz de Control (coeficientes asociados de la entrada).
C - Matriz de Observación (coeficientes asociados a la salida).
D - Matriz de transferencia directa entrada-salida.
y - Matriz de salidas del sistema
1.2 Simbología
Con la finalidad de facilitar el análisis de los sistemas de control, estos son representados mediante diagramas de bloques, permitiendo visualizar las relaciones entre los componentes del sistema y las señales que fluyen en dicho sistema.
Los componentes principales de un sistema de control son:
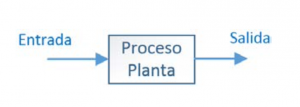
Figura 1.1. Sistema de una entrada y una salida
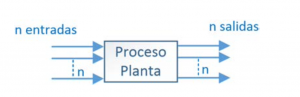
Figura 1.2 Sistema de n entradas y n salidas
Con la finalidad de facilitar el análisis de los sistemas de control, estos son representados mediante diagramas de bloques, permitiendo visualizar las relaciones entre los componentes del sistema y las señales que fluyen en dicho sistema.
Los componentes principales de un sistema de control son: