Cálculo de Varias Variables
Ecuaciones Paramétricas
Cuando necesitamos representar una trayectoria de un robot móvil , debemos usar las ecuaciones paramétricas. En las ecuaciones paramétricas los puntos de la función están dados por los puntos (x ,y) en función de una variable independiente, por ejemplo t , que representa al tiempo.
Usando MATLAB o cualquier otra plataforma que grafique funciones paramétricas podemos graficar una
circunferencia.
Ejemplo: Codigo de MATLAB para graficar una circunferencia
clearvars;
t=linspace(0,2*pi,100); % Definimos el rango
x=cos(t); % Ecuación paramétrica de x en funcioón de t
y=sin(t); % Ecuación paramétrica de y en funcion de t
plot(x,y) ,axis equal; % Instrucción de graficar y mostrar los ejes en proporción 1:1
Ejemplos de gráficos de ecuaciones paramétricas
F1
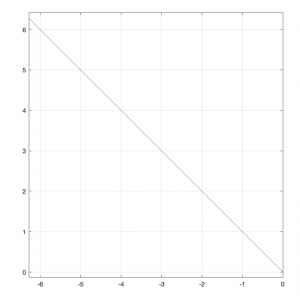
F2
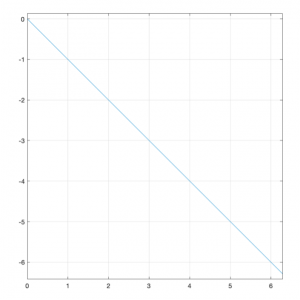
F3
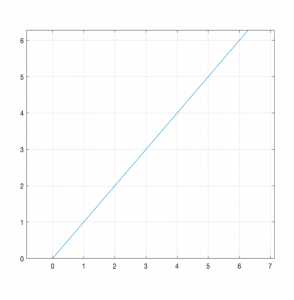
F2
F4
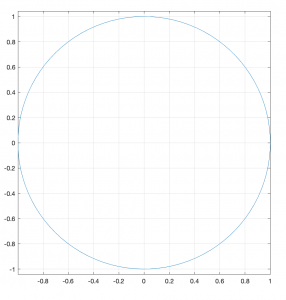
F5
F1
F6

F1
F7
F8
F9
Encontrar la Correspondencia de la función paramétrica con el Gráfico del F1 al F9
x = t ; y = -t
x = t ; y = t
x = cos(t). ; y = sin(t)f
x = -t ; y = t
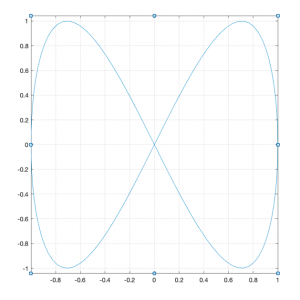
x = cos(t) ; y= sin(2t)
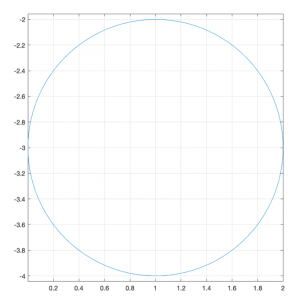
x = cos(t) + 1 ; y = sin(t)
x = cos(t) + 1 ; y = sin(t) – 3x=sen t+21 cos 5t+41 sen 13t ; y=cos t+21 sen 5t+41 cos 13t
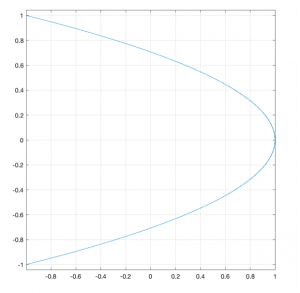
x = cos(2t). ; y = sin(t)
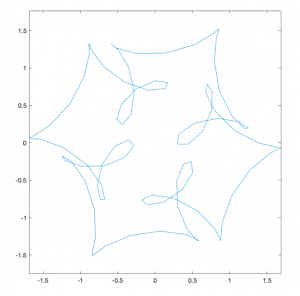
x=sen t - 21 cos 5t - 41 sen 13t ; y=cos t+21 sen 5t+41 cos 13t
