cl1-03. Rango de una Matriz

---

Definición. Sea A una matriz m\times n, el rango de A es el número de filas no nulas que resultan luego de reducir por renglones a la matriz.

Notación. Se denota el rango de la matriz A como \rho\left(A\right), Rg\left(A\right) o r\left(A\right).

 

Ejemplo 1. Dada la matriz A=\scriptsize{\left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\ 3 & 1 & 2 & 0 \\ -2 & 1 & -3 & 1 \end{array}\right)}, calcule su rango.

Solución.

\left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\ 3 & 1 & 2 & 0 \\ -2 & 1 & -3 & 1 \end{array}\right)
\begin{array}{c} {\scriptsize f_{2}-3f_{1}} \\ \longrightarrow \\ {\scriptsize f_{3}+2f_{1}}\end{array}
\left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\ 0 & -5 & 5 & -3 \\ 0 & 5 & -5 & 3 \end{array}\right)
\stackrel{f_{3}+f_{2}}{\longrightarrow}
\left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\ 0 & -5 & 5 & -3 \\ 0 & 0 & 0 & 0 \end{array}\right)

Por consiguiente, el rango de la matriz A es 2.

Aplicación en el análisis de los sistemas de ecuaciones lineales

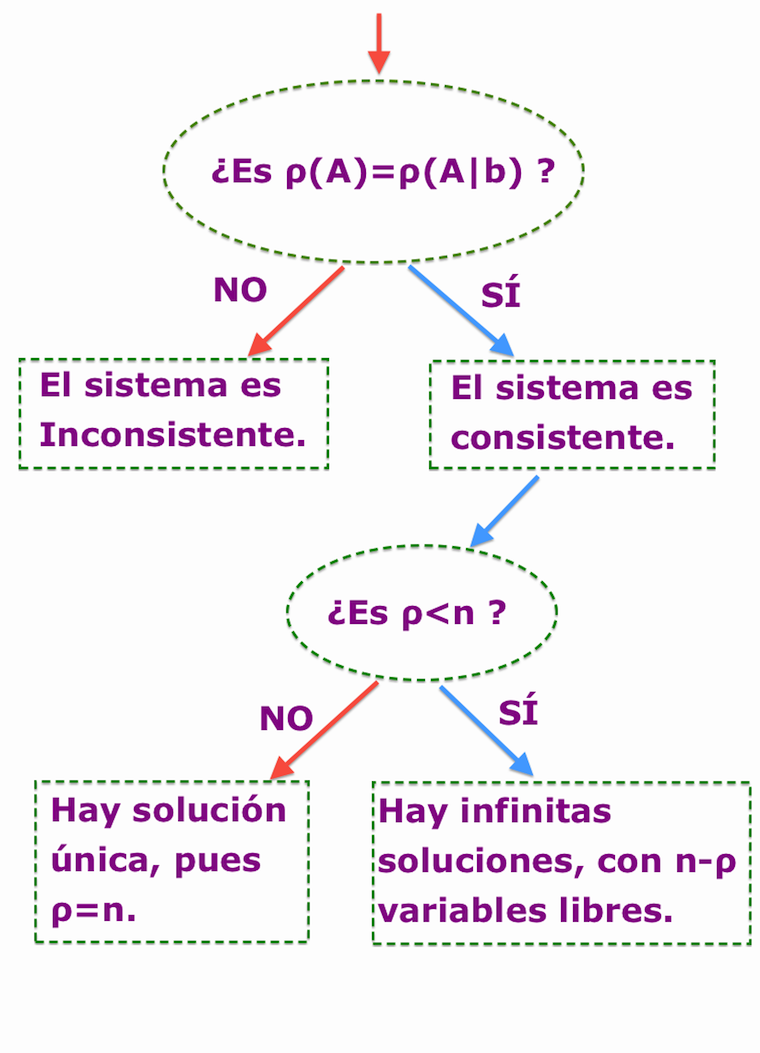
Teorema de Kronecker-Capelli. Sea el sistema de ecuaciones lineales Ax=b, entonces el sistema es consistente (o compatible) si y solo si el rango de A es igual al rango de la matriz aumentada \left(A|b\right); es decir \rho\left(A\right)=\rho\left(A|b\right)

Ejemplo 2. Analice el siguiente sistema de ecuaciones lineales: \left\{ \begin{array}{rcrcrcl}
x&+&2y&-&z&+&w&=&5 \\
3x&+&y&+&2z&& &=&2 \\
-2x&+&y&-&3z&+&w&=&3 
\end{array}\right.

Solución. La representación matricial del sistema Ax=b es \left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\3 & 1 & 2 & 0 \\ -2 & 1 & -3 & 1 \end{array}\right)\left(\begin{array}{c}x\\y\\z\\w \end{array}\right)=\left(\begin{array}{c}5\\2\\3 \end{array}\right)donde A=\scriptsize{\left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\3 & 1 & 2 & 0 \\ -2 & 1 & -3 & 1 \end{array}\right)} y b=\scriptsize{\left(\begin{array}{c}5\\2\\3 \end{array}\right)}.

La representación con matriz aumentada \left(A|b\right) es \left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\3 & 1 & 2 & 0&2 \\ -2 & 1 & -3 & 1 &3\end{array}\right)y su resolución mediante operaciones de renglón (forma escalonada) es

\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 3 & 1 & 2 & 0&2 \\ -2 & 1 & -3 & 1 &3\end{array}\right)
\begin{array}{c} {\scriptsize f_{2}-3f_{1}} \\ \longrightarrow \\ {\scriptsize f_{3}+2f_{1}}\end{array}
\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 0 & -5 & 5 & -3 &-13\\ 0 & 5 & -5 & 3 &13\end{array}\right)
\stackrel{f_{3}+f_{2}}{\longrightarrow}
\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 0 & -5 & 5 & -3 &-13\\ 0 & 0 & 0 & 0 &0\end{array}\right)

donde se observa que el rango de la matriz aumentada \left(A|b\right) es 2. De la misma manera, al omitir la matriz b y analizar, se observa que el rango de A también es 2, es decir\rho \left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 0 & -5 & 5 & -3 &-13\\ 0 & 0 & 0 & 0 &0\end{array}\right)=\rho \left(\begin{array}{rrrr}1 & 2 & -1 & 1 \\ 0 & -5 & 5 & -3\\ 0 & 0 & 0 & 0\end{array}\right)Por consiguiente, el sistema de ecuaciones lineales es consistente.

Ejemplo 3. Analice el sistema de ecuaciones lineales del ejemplo previo que ha sido modificado como: 
\left\{ \begin{array}{rcrcrcl}x&+&2y&-&z&+&w&=&4 \\
3x&+&y&+&2z&& &=&1 \\
-2x&+&y&-&3z&+&w&=&1 
\end{array}\right.

Solución. La representación con matriz aumentada y su resolución mediante operaciones de renglón (forma escalonada) es

\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &4\\ 3 & 1 & 2 & 0&1 \\ -2 & 1 & -3 & 1 &1\end{array}\right)
\begin{array}{c} {\scriptsize f_{2}-3f_{1}} \\ \longrightarrow \\ {\scriptsize f_{3}+2f_{1}}\end{array}
\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 0 & -5 & 5 & -3 &-11\\ 0 & 5 & -5 & 3 &9\end{array}\right)
\stackrel{f_{3}+f_{2}}{\longrightarrow}
\left(\begin{array}{rrrr|r}1 & 2 & -1 & 1 &5\\ 0 & -5 & 5 & -3 &-11\\ 0 & 0 & 0 & 0 &2\end{array}\right)

donde se puede observar que la matriz aumentada \left(A|b\right) tiene rango 3, pero al omitir la aumentada b, se obtiene que el rango de A es 2. Por consiguiente, el sistema de ecuaciones lineales es inconsistente.

El rango provee además información sobre el tipo de solución cuando un sistema de ecuaciones lineales \left(A|b\right) es consistente. El número de incógnitas es el número de columnas n de la matriz A, mientras que el número de variables libres es igual a n-\rho. En consecuencia, un sistema de ecuaciones lineales consistente tiene infinitas soluciones, si y solo si, n-\rho es mayor que cero \left(n>\rho\right), pero tiene solución única si n=\rho.

En el sistema de ecuaciones lineales consistente del Ejemplo 2, se tiene que \rho=2 pero el número de incógnitas es n=4. Luego, la cantidad de variables libres es n-\rho=2 y el sistema de ecuaciones lineales tiene infinitas soluciones.

Ejemplo 4. Analice el siguiente sistema de ecuaciones lineales aplicando el concepto de rango: 
\left\{ \begin{array}{rcrcl}2x&-&3y&=&6 \\
x&-&3y&=&0 \\
3x&-&3y&=&12 
\end{array}\right.

Solución. La representación con matriz aumentada y su resolución mediante operaciones de renglón (forma escalonada) es

\left(\begin{array}{rr|r} 2 & -3 & 6\\ 1 & -3 & 0\\ 3 & -3 & 12 \end{array}\right) \begin{array}{c} \stackrel{f_{1} {\leftrightarrow} f_{2}}{\longrightarrow} \end{array}\left(\begin{array}{rr|r}1 & -3 & 0\\2 & -3 & 6\\3 & -3 & 12\end{array}\right) \begin{array}{c} {\scriptsize f_{2}-2f_{1}} \\ \longrightarrow \\ {\scriptsize f_{3}-3f_{1}}\end{array} \left(\begin{array}{rr|r} 1 & -3 & 0\\0 & 3 & 6\\0 & 6 & 12\end{array}\right) \stackrel{f_{3}-2f_{2}}{\longrightarrow}\left(\begin{array}{rr|r}1 & -3 & 0\\0 & 3 & 6\\0 & 0 & 0\end{array}\right) 

donde se puede observar que \rho\left(A|b\right)=\rho\left(A\right). Por consiguiente, el sistema de ecuaciones lineales es consistente.

El número de incógnitas es 2, y el rango es 2, por consiguiente, el sistema de ecuaciones lineales tiene solución única, pues la cantidad de variables libres es n-\rho=0.

---

Enlaces de interés

Clase Online
Plataforma SIDWeb
Referencias Bibliográficas