Referencia: Lathi 2.1 p151, Hsu 2.5.B p60, Oppenheim 2.14 p118
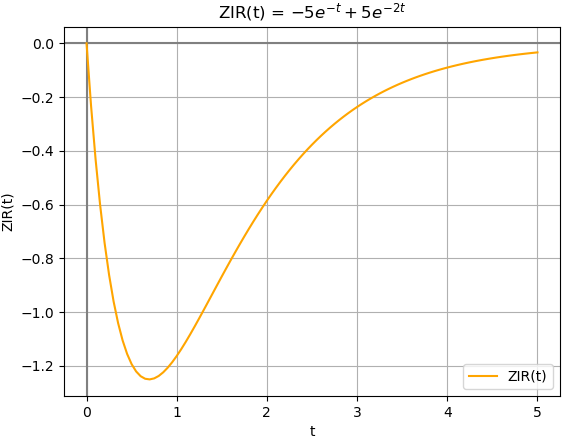
La respuesta a entrada cero de un sistema se obtiene aplicando x(t)=0 en la ecuación diferencial lineal, es decir no se le aplica una señal de entrada. La respuesta a entrada cero, Zero Input Response (ZIR), también es conocida como la solución a la ecuación diferencial homogénea, en la que x(t)=0.
| Respuesta total |
= | respuesta a entrada cero ZIR |
+ | respuesta a estado cero ZSR |
La respuesta a entrada cero permite observar las condiciones internas del sistema, cargas en capacitores o corrientes en inductores como energía residual de los estados anteriores al de observación.
La ecuación diferencial lineal homogénea se obtiene también hacer x(t)=0, de una forma:
a_0 \frac{d^2}{dt^2}y(t) +a_1\frac{d}{dt}y(t) + a_2y(t) = 0Ejemplo 1. Respuesta a entrada cero ZIR para un sistema LTI CT – Desarrollo analítico
Referencia: Lathi Ejemplo 2.1.a p155, Oppenheim ej2.14 p118, ejemplo 1 de Modelo entrada-salida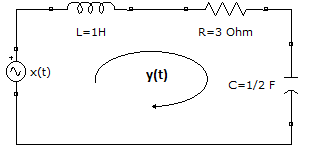
Encuentre la respuesta a entrada cero (ZIR) para el sistema LTI CT del circuito RLC, descrito por la ecuación diferencial lineal:
\frac{d^{2}y(t)}{dt^{2}} + 3\frac{dy(t)}{dt} + 2y(t) = \frac{dx(t)}{dt} (D^2 + 3D +2)y(t) = Dx(t)con las condiciones o valores iniciales descritos por: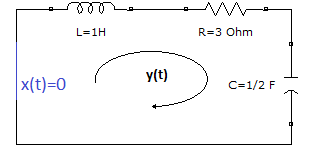
y0(t) =0
y’0(t) =-5
La entrada cero del circuito, x(t)=0 convierte la ecuación lineal en homogénea. Para entrada cero se usa x(t)=0, se quita la fuente y se cierra el circuito para observar lo que hace el sistema sin señal de entrada.
\frac{d^{2}y(t)}{dt^{2}} + 3\frac{dy(t)}{dt} + 2y(t) = 0 (D^2 + 3D +2)y(t) = 0Siendo el sistema LTI descrito por los polinomios de operadores D descritos como Q(D) y P(D), la ecuación se simplifica al eliminar P(D):
Q(D) y(t) = P(D) x(t) (D^2 + 3D +2)y(t) = 0Q(D) es la ecuación característica o auxiliar del sistema:
\lambda ^2 + 3\lambda +2 = 0Al buscar las raíces de λ, se escribe la ecuación en sus factores y se puede buscar los modos característicos,
(\lambda +1)(\lambda + 2) = 0| Raíces características | Modos característicos |
| λ1 = -1 | e-t |
| λ2 = -2 | e-2t |
Con los modos característicos se plantea la solución general y0(t) como la suma de los modos característicos con coeficientes aún por determinar.
y_0 (t) = c_1 e^{-t} + c_2 e^{-2t}Para determinar los valores de las constantes c1 y c2 se aplican las condiciones iniciales para t0=0. Del enunciado del ejercicio se tiene que No hay señal en la salida al tiempo cero y(0)=0, además que la variación es negativa y'(0)=-5:
Las restricciones indicadas también son conocidas como condiciones auxiliares, solo cuando estas condiciones son dadas para t=0 se denominan condiciones iniciales o valores iniciales (Lathi p161).
En la primera condición con t=0, la salida:
y_0 (0) = 0 y(t)\Big|_{t=0} = c_1 e^{-0} + c_2 e^{-2(0)} c_1+c_2 = 0en el caso para la condición de primera derivada:
y'_0 (0) = -5 y'_0(t)\Big|_{t=0} = \frac{d}{dt}\Big[ c_1 e^{-t} + c_2 e^{-2t}\Big]\Big|_{t=0} =\Big[ -c_1 e^{-t} -2c_2 e^{-2t}\Big] \Big|_{t=0} = -c_1 e^{-0} -2c_2 e^{-2(0)} -c_1 -2c_2 = -5Con lo que con la evaluación de las condiciones iniciales se tiene que:
\begin{cases} c_1 + c_2 = 0\\ -c_1 - 2c_2 = -5 \end{cases}se resuelve obteniendo: c1 = -5 ; c2 = 5,
que al sustituir en la ecuación anterior, se encuentra la respuesta a entrada cero ZIR:
La gráfica muestra el sentido de la corriente, usando la carga residual del capacitor dentro del circuito, a pesar de no tener señal de entrada a partir del tiempo 0 hasta 5:
Cálculos numéricos con Python
Para determinar los valores de las constantes, se puede usar algunas instrucciones sencillas con Numpy. Para las raíces del polinomio se usan solo los coeficientes de operadores D, ordenados de grado mayor a menor.
D^2 + 3D +2 = 0import numpy as np >>> np.roots([1,3,2]) array([-2., -1.])
Para los coeficientes se plantean las ecuaciones de la forma matricial Ax=B:
\begin{cases} c_1 + c_2 = 0\\ -c_1 - 2c_2 = -5 \end{cases}>>> A = [[ 1, 1], [-1,-2]] >>> B = [ 0,-5] >>> np.linalg.solve(A,B) array([-5., 5.]) >>>
Respuesta entrada cero: [Desarrollo Analítico] [Sympy-Python] [Scipy-Python] [Runge-Kutta d2y/dx2] [Simulador]
Solución general de ecuación auxiliar ay»+by’+c =0
Referencia: Stewart James. Cálculo de varias variables. 17.1 p1147 pdf544
| Raíces de la ecuación característica | solución general |
|---|---|
| raices reales y distintas \lambda_1 , \lambda_2 | y=c_1 e^{\lambda_1 t}+c_2 e^{\lambda_2 t} |
| raíces iguales \lambda_1 = \lambda_2 = \lambda | y=c_1 e^{\lambda t}+c_2 t e^{\lambda t} |
| raíces complejas \alpha \pm i\beta | y= e^{\alpha t}(c_1 \cos{\beta t}+c_2 \sin{\beta t}) |