Referencia: Lathi 2.4 p168, Oppenheim 2.2.2 p94 , Hsu 2.5.B p60
El estado cero del sistema, «Zero-State», supone no hay energía almacenada, que los capacitores están descargados, que recien sale el equipo de la caja. Para éste caso, la respuesta del sistema se conoce como respuesta a estado cero, «Zero-State Response» ZSR.

| Respuesta total |
= | respuesta a entrada cero |
+ | respuesta a estado cero |
| ZSR = h(t) ⊗ x(t) |
Para los problemas presentados se asume que el sistema es lineal, causal e invariante en el tiempo. En la práctica, muchos de los sistemas son causales, pues su respuesta no inicia antes de aplicar una entrada, es decir, todas las entradas a evaluar empiezan en t=0.
La respuesta del sistema y(t) para un LTIC se determina con la convolución entre x(t) y h(t), definida mediante el operador ⊗ como :
y(t) = x(t) \circledast h(t) = \int_{-\infty}^{+\infty} x(\tau)h(t-\tau) \delta \tauEs importante observar que el integral de convolución se realiza con respecto a τ en lugar de t.
Si h(t) es causal, lineal, continua
Es decir, multiplicada por μ(t), se tiene que, h(t)=0 para t<0 y el integral puede expresarse como:
y(t) = \int_{-\infty}^{+\infty} h(\tau)\mu (\tau) x(t-\tau) \delta \tau = \int_{0}^{\infty} h(\tau) x(t-\tau) \delta \tauO de forma alterna, aplicando la condición de causalidad (Oppenheim 2.3.6 p112)
y(t) = \int_{0}^{\infty} h(\tau) x(t-\tau) \delta \tau = \int_{-\infty}^{t} x(\tau) h(t-\tau) \delta \tauSi la entrada x(t) y el sistema h(t) son causales
la respuesta también será causal.
y(t)=\begin{cases}\int_{0^{-}}^{t} x(\tau)h(t-\tau) \delta \tau , & t\ge 0\\ 0, & t<0 \end{cases} y(t)=\int_{0^{-}}^{t} x(\tau)h(t-\tau) \delta \tau = \int_{0^{-}}^{t} h(\tau)x(t-\tau) \delta \tauEl límite inferior del integral se usa como 0–, implica aunque se escriba solo 0 se pretende evitar la dificultad cuando x(t) tiene un impulso en el origen.
Recordar que, basado en la condición de causalidad, si x(t)=0 para t<0, esta señal es causal. En el caso contrario, si x(t)=0 para t>0 la señal es No causal o anticausal.
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
Ejemplo 1. Respuesta Estado Cero ZSR con h(t) causal y x(t) causal
Referencia: Lathi ejemplo 2.6 p166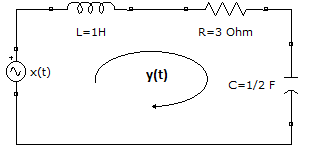
Encuentre la corriente y(t) del circuito RLC, cuando todas las condiciones iniciales son cero y en la entrada se tiene la señal x(t) descrita por:
x(t) = 10 e^{-3t} \mu (t)Además el sistema tiene respuesta a impulso:
h(t) = \big( 2e^{-2t} -e^{-t}\big)\mu (t)El ejemplo es la continuación del presentado para respuesta a entrada cero ZIR, que tiene la ecuación:
(D^2 + 3D +2)y(t) = Dx(t)Desarrollo Analítico
La respuesta se obtiene aplicando convolución entre la señal de entrada x(t) y la respuesta al impulso h(t) del sistema:
y(t) = x(t) \circledast h(t) = [ 10 e^{-3t} \mu (t)] \circledast [(2e^{-2t} - e^{-t}) \mu (t)]usando la propiedad distributiva de la convolución:
y(t) = [10e^{-3t} \mu (t) \circledast 2e^{-2t} \mu (t)] - [10e^{-3t} \mu (t) \circledast e^{-t} \mu (t)] = 20[e^{-3t}\mu (t) \circledast e^{-2t} \mu (t)] - 10[e^{-3t} \mu(t) \circledast e^{-t} \mu (t)]Para éste ejercicio se usa la tabla de integrales convolución, línea 4, asi el enfoque del desarrrollo se mantiene sobre la forma de la señal resultante. El siguiente ejemplo se desarrolla con el integral de convolución.
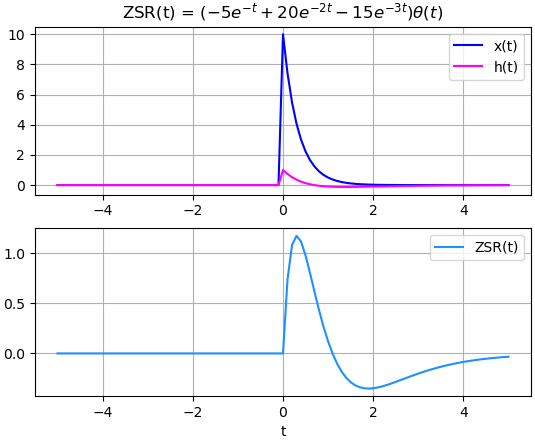
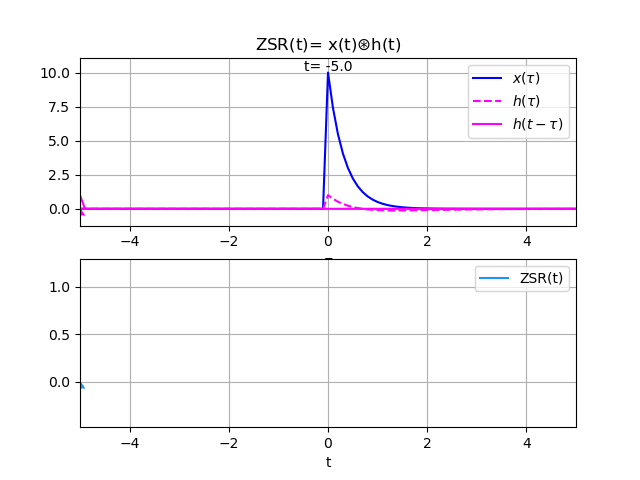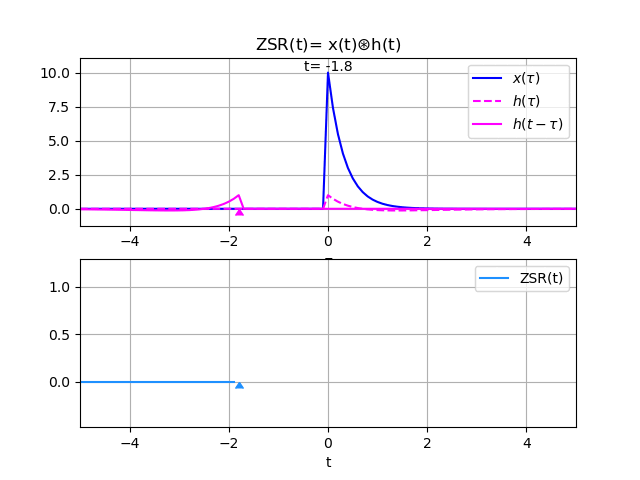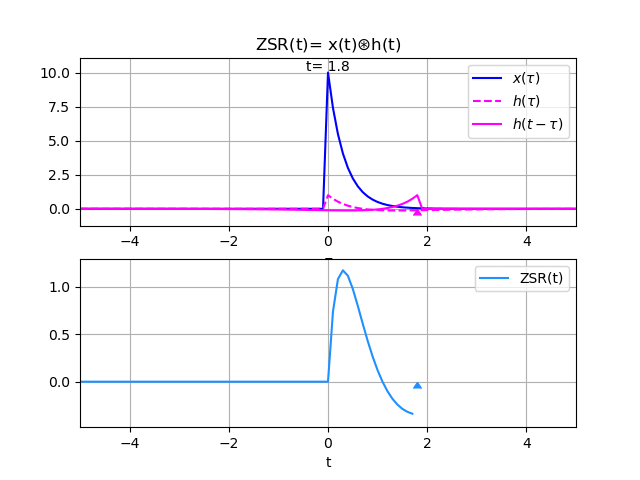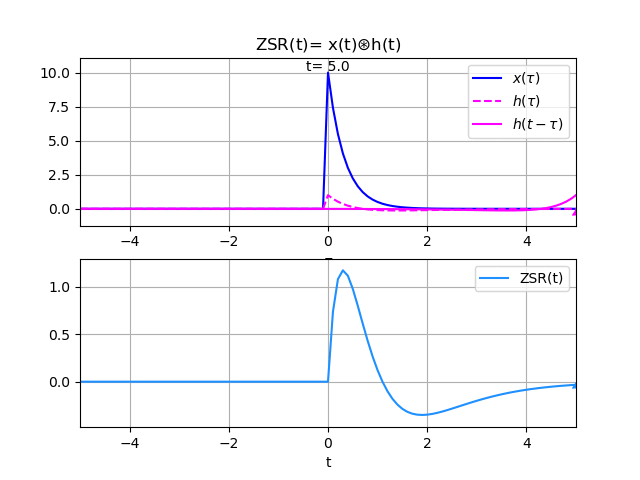
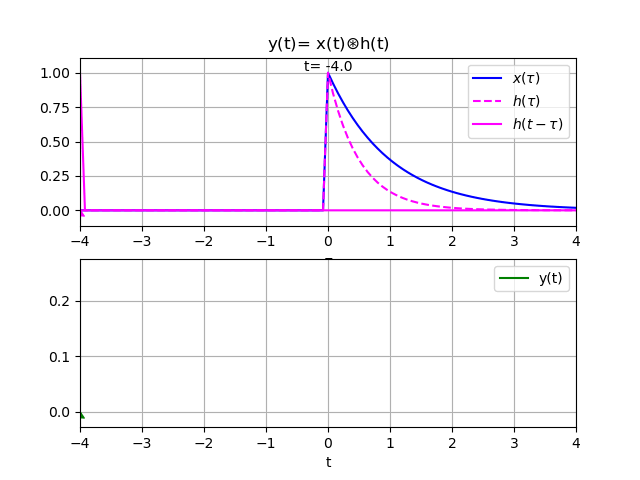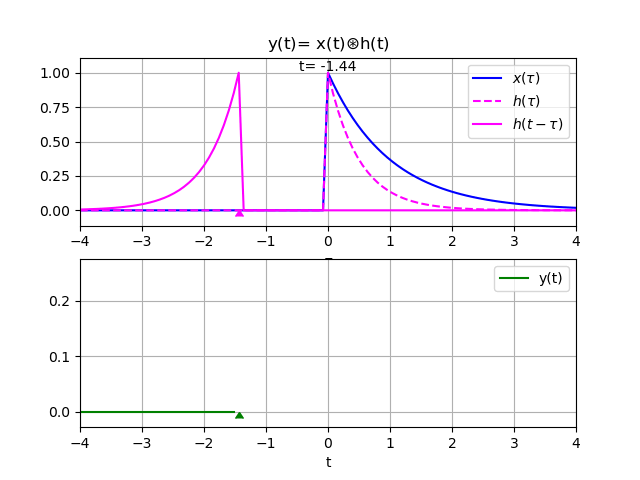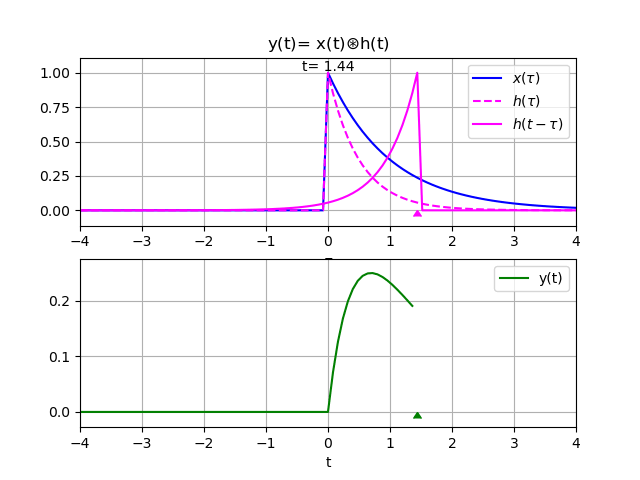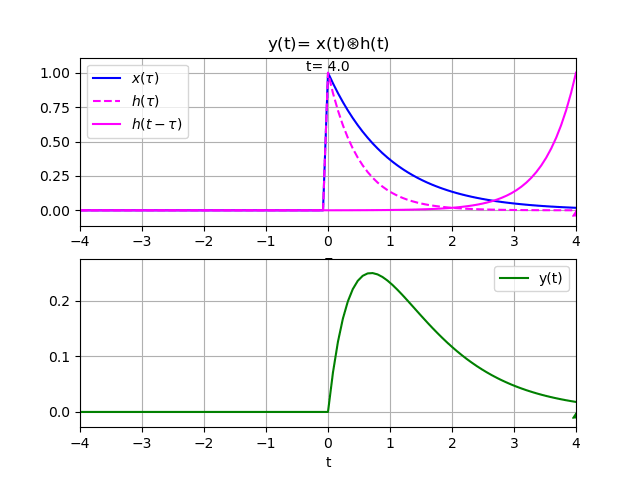
y(t) = 20\frac{e^{-3t} - e^{-2t}}{-3-(-2)}\mu (t) - 10\frac{e^{-3t} - e^{-t}}{-3-(-1)}\mu (t) y(t) = 20\frac{e^{-3t} - e^{-2t}}{-3+2}\mu (t) - 10\frac{e^{-3t} - e^{-t}}{-3+1}\mu (t) = -20\big[e^{-3t} - e^{-2t}\big]\mu (t) + 5\big[e^{-3t} - e^{-t}\big]\mu (t) = \big[-5e^{-t} + 20e^{-2t} - 15e^{-3t}\big]\mu (t)De las gráficas se observa que la entrada es semejante a conectar en la entrada un capacitor con carga, que la pierde en el tiempo.
En la salida se observa el efecto, la parte inicial corresponde a la corriente en el circuito mientras el capacitor de la entrada entrega energía al sistema. Note que en el sistema o circuito se debe ir cargando el capacitor del sistema. Luego, un poco más del segundo 1, la corriente invierte el sentido volviéndose negativa por la carga almacenada en el capacitor del sistema.
La explicación breve realizada debería ser comprobada en los experimentos de laboratorio, preferiblemente a escala menor con componentes tipo electrónico.
Proponer como tarea.
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
Ejemplo 2. Respuesta Estado Cero ZSR con h(t) causal y x(t) causal
Referencia: Lathi Ejemplo 2.8 p173
Para un sistema LTIC, si la respuesta al impulso es
h(t) = e^{-2t} \mu (t)determine la respuesta y(t) para la entrada
x(t) = e^{-t} \mu (t)Desarrollo Analítico
Para éste ejercicio se desarrollará la integral de convolución. La entrada y respuesta al impulso se convierte a:
x(\tau) = e^{-\tau} \mu(\tau) h(t-\tau) = e^{-2(t-\tau)} \mu(t-\tau)recuerde que la integración es respecto a τ enel intervalo 0≤τ≤t.
y(t) = \begin{cases} \int_{0}^{t} \Big[e^{-\tau}\mu(\tau) e^{-2(t-\tau)}\mu(t-\tau)\Big] \delta\tau , & t\ge 0 \\0, & t \lt 0 \end{cases}Los valores de u(τ) =1 debido a se convierte a 0 para τ<0 y en el caso de u(t-τ)=1 se convierte a 0 cuando τ≥t.
y(t) = \int_{0}^{t}e^{-\tau} e^{-2(t-\tau)} \delta\tau = \int_{0}^{t} e^{-\tau} e^{-2t} e^{2\tau} \delta\tau = e^{-2t} \int_{0}^{t} e^{\tau} \delta\tau = e^{-2t} e^{\tau} \Big|_0^t = e^{-2t} (e^{t} - 1) = e^{-t} - e^{-2t}para t≥0, y además como y(t) = 0 para t<0
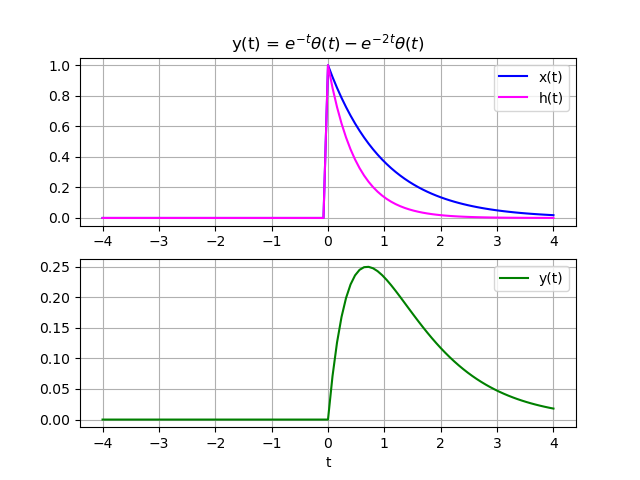
y(t) = \big( e^{-t} - e^{-2t} \big) \mu(t)Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]
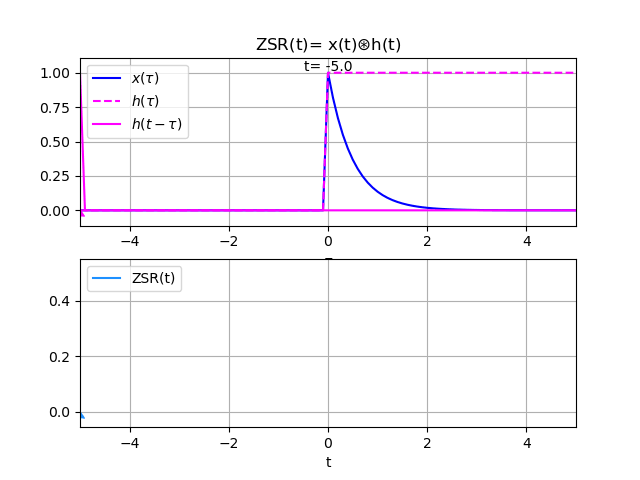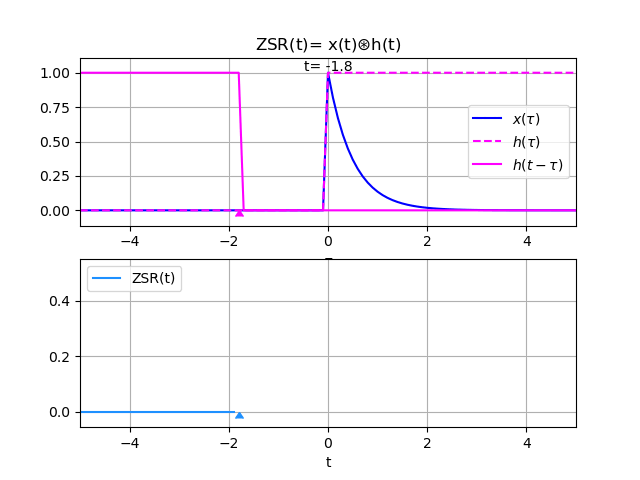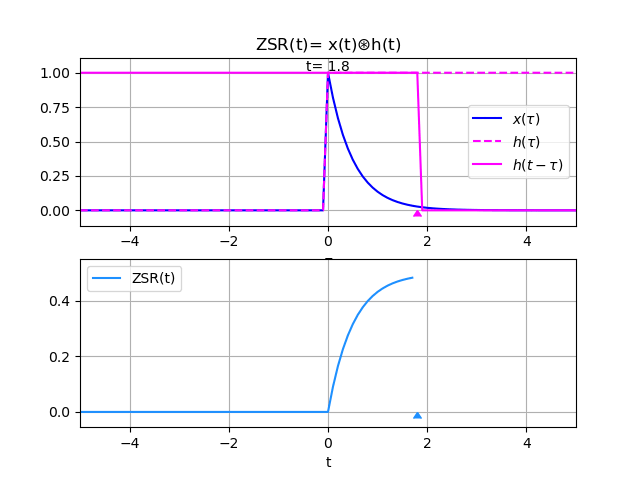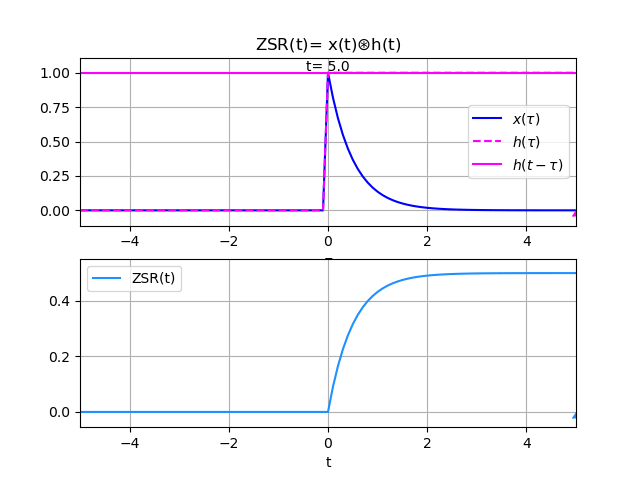
Ejemplo 3. Respuesta entrada cero ZSR entre exponencial y escalón unitario
Referencia: Oppenheim Ejemplo 2.6 p98
Sea x(t) la entrada a un sistema LTI con respuesta a impulso unitario h(t),
x(t) = e^{-at} \mu (t) \text{ , } a>0 h(t) = u(t)dado que la señal de entrada tiene valores para t≥0 al tener un componente μ(t), se tiene que:
y(t) = \int_{0}^{t} x(\tau)h(t-\tau) \delta \tau x(\tau) = e^{-a\tau} \mu (\tau) h(t-\tau) = \mu (t-\tau)observando que en la región de integración sobre τ se encuentra [0,t], entonces τ≥0 se tiene que μ(τ)=1 y para t-τ≥0 se tiene también que μ(t-τ) = 1.
y(t) = \int_{0}^{t} e^{-a\tau} \delta \tau = -\frac{1}{a} e^{-a\tau} \Big|_0^t = -\frac{1}{a}(e^{-at}-e^{0}) y(t) = \frac{1}{a}(1 - e^{-at})recordando que esta definido para t≥0
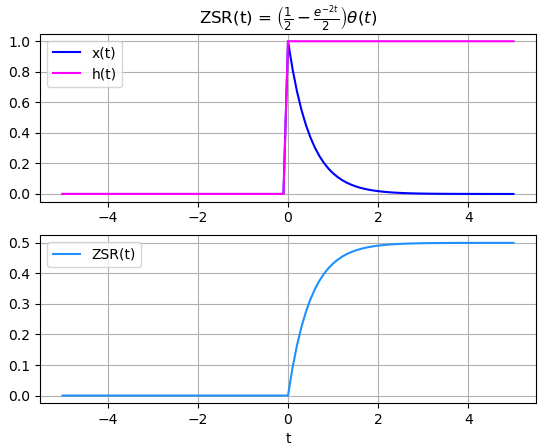
y(t) = \frac{1}{a}(1 - e^{-at}) \mu (t)Para la gráfica, se define a=2 y se obtiene,
El proceso de convolución se observa en la animación realizada al desplazar el varo de tau
Respuesta estado cero: [Desarrollo Analítico] [Scipy-Python] [Numpy-Convolución] [algoritmo Python-Convolución] [Simulador]