U5videos Sistemas LTI – Fourier
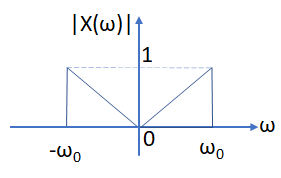
3Eva2016TI_T4 rampa(ω) – transformada inversa de Fourier
3Eva2016TI_T3 LTI CT Circuito RL respuesta de frecuencia
3ra Evaluación I Término 2016-2017. 15/septiembre/2016 TELG1001
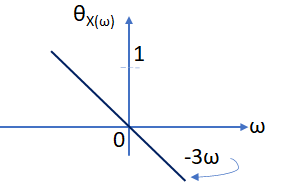
Tema 3. (26 puntos) Para el circuito eléctrico que se muestra en la siguiente figura:
a. Determinar su función de transferencia
b. Determinar, esquematizar y etiquetar su respuesta de frecuencia, indicando a que tipo de filtro no ideal de frecuencias selectivas se podría asociar su comportamiento.
c. Obtener la respuesta impulso h(t) que representa al circuito eléctrico.
d. Determinar la respuesta v2(t) que se obtiene a la salida de dicho sistema cuando es exitado con una entrada v1(t) = sen 50t [V].
¿Qué puede decir acerca de si el sistema transmite con distorsión o sin distorsión? Justifique su respuesta de manera razonada.
Coordinador: Tama Alberto
3Eva2016TI_T2 LTI CT Sub-sistemas h(t) multiplicados con Fourier
3ra Evaluación I Término 2016-2017. 15/septiembre/2016 TELG1001
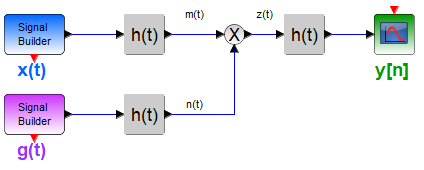
Tema 2. (26 puntos) Considere el sistema mostrado en la siguiente figura, donde la respuesta impulso h(t) está dada por:
h(t) = \frac{\sin (11 \pi t)}{\pi t} x(t) = \sum_{k=1}^{\infty} \frac{1}{k^2} \cos (5k \pi t) g(t) = \sum_{k=1}^{10} \cos (8k \pi t)a. Determinar la energía contenida en la señal h(t)
b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal m(t). Es decir M(ω) vs ω.
c. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal n(t). Es decir N(ω) vs ω.
d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.
Coordinador: Tama Alberto
3Eva2016TI_T1 LTI DT h[n] con subsistemas de bloques en paralelo
3ra Evaluación I Término 2016-2017. 15/septiembre/2016 TELG1001
Tema 1. (26 puntos) Un sistema LTI-DT está integrado por la conexión en paralelo de dos subsistemas retroalimentados, tal como se muestra en la figura.
Determinar:
a. Las respuestas impulso de cada subsistema y del sistema completo, es decir h1[n], h2[n], h[n]
b. Comente sobre la estabilidad de cada subsistema y del sistema completo, justificando debidamente su respuesta.
c. La respuesta y[n] (expresada a la mínima expresión) frente a la entrada
x[n] = e^{-0.5n} \mu [n]Nota: Realizar el desarrollo en el Dominio del Tiempo Discreto o en el dominio de la Frecuencia Compleja z. Al final , la respuesta deberá ser la misma- Aquí se procederá a resolverlo utilizando las técnicas referidas al Dominio del tiempo discreto.
Coordinador: Tama Alberto
3Eva2016TII_T4 Espectro de señales con Fourier
3ra Evaluación II Término 2016-2017. 2/Marzo/2017. TELG1001
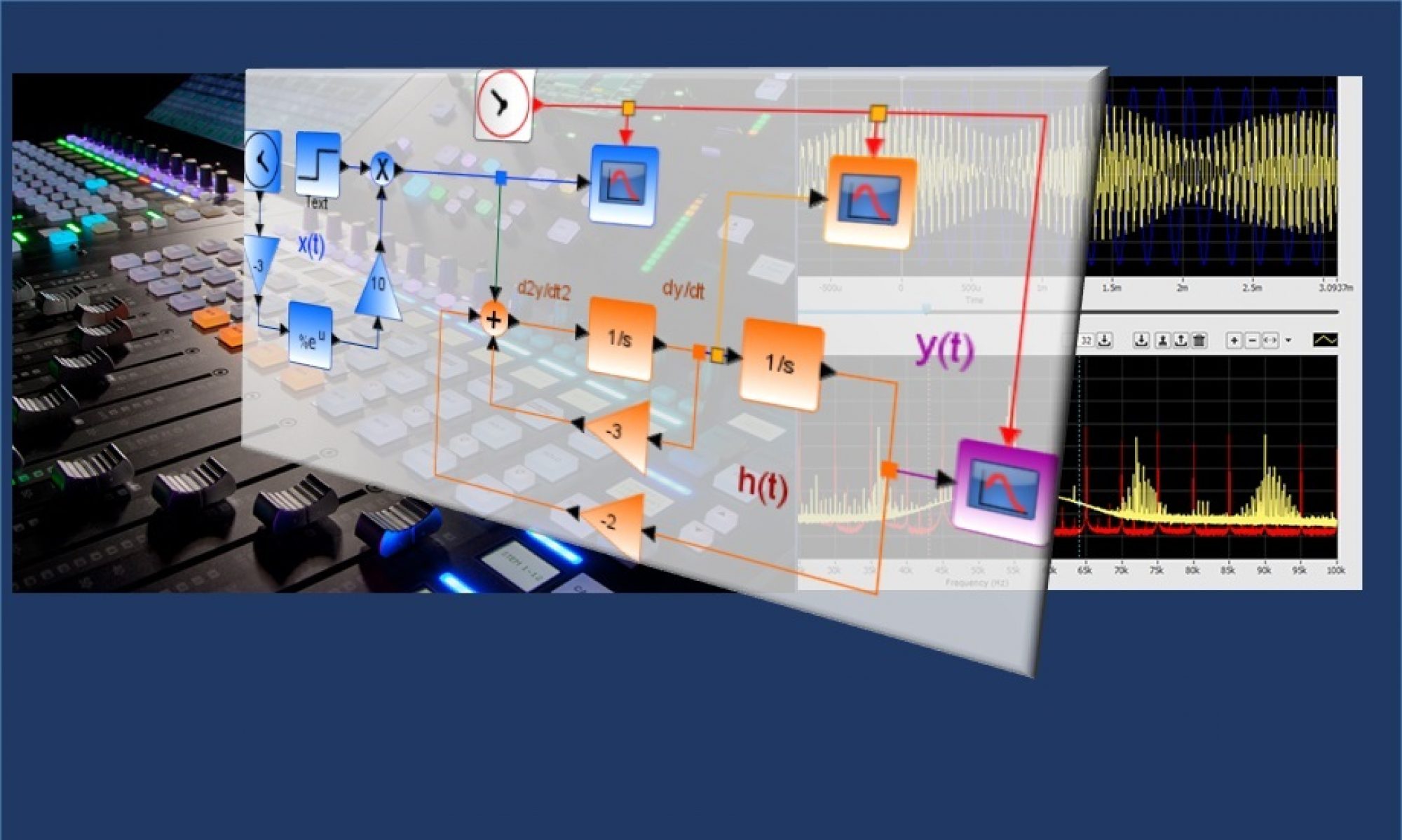
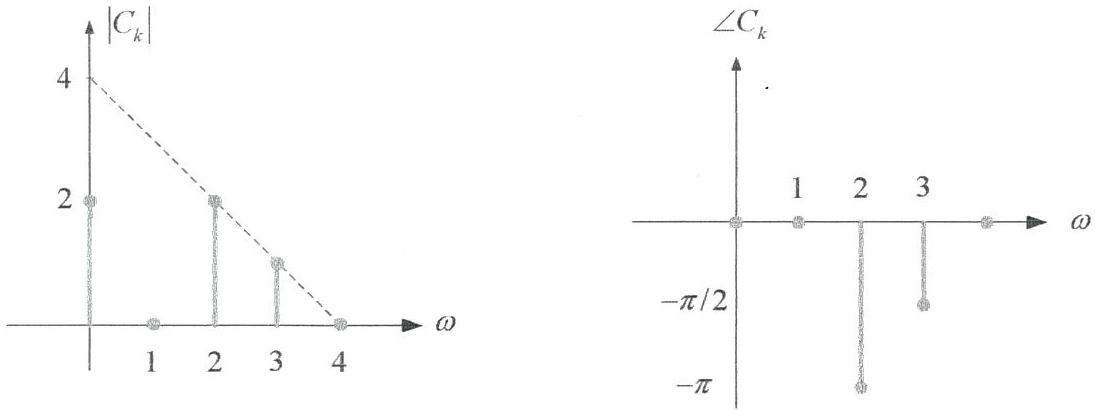
Tema 4. (24 puntos) La siguiente figura muestra el especrto de Fourier de una señal periódica x(t).
a. Por simple inspección, determine las Series de Fourier (armónica) que representan a x(t)
b. Por simple inspección, esquematice adecuadamente el espectro de los coeficientes de Fourier complejos exponenciales.
c. Encuentre la potencia y Energía de la señal x(t).
Coordinador: Tama Alberto
3Eva2016TII_T3 LTI CT con Fourier
3ra Evaluación II Término 2016-2017. 2/Marzo/2017. TELG1001
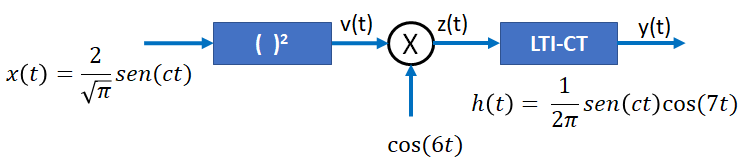
Tema 3. (28 puntos) La señal de entrada x(t) es aplicada a un dispositivo cuadratizador. Así mismo, la respuesta v(t) del dispositivo es modulada con una señal sinusoidal como se muestra en la figura. Finalmente, la señal de salida z(t) es aplicada a un sistema LTI-CT cuya respuesta al impulso se especifica en el diagrama.
a. Determinar, esquematizar y etiquetar la transformada de Fourier de v(t), es decir V(ω) y obtener el valor de la energía de v(t), es decir Ev(t).
b. Determinar, esquematizar y etiquetar la transformada de Fourier de z(t), es decir Z(ω) y obtener el valor de la energía de z(t), es decir Ez(t).
c. Indicar de manera justificada, el comportamiento del sistema LTI-CT a que tipo de filtro ideal de frecuencias selectivas corresponde. Determinar, esquematizar y etiquetar la respuesta de freciencia del referido sistema.
d. Encontrar el valor de la respuesta y(t) y obtener el valor de su energía, es decir Ey(t).
Coordinador: Tama Alberto
3Eva2016TII_T2 Sistemas LTI DT en Cascada
3ra Evaluación II Término 2016-2017. 2/Marzo/2017. TELG1001
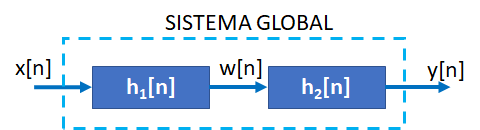
Tema 2. (24 puntos) Dos sistemas LTI-DT causales, tienen respuesta impulso h1[n] y h2[n] respectivamente. Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de confirmar un sistema global. El esquema se muestra en la figura.
Las ecuaciones de diferencia que relacionan a cada sub-sistema y al global son las siguientes:
S1: w[n] = \frac{1}{2}w[n-1] + x[n] S2: y[n] = \beta w[n] + w[n-1]- \alpha y[n-1] SG: y[n] = -\frac{1}{10}y[n-2] - \frac{7}{10}y[n-1]+x[n-1]Usando la transformada z
a. Determinar los valores de α y β.
b. Obtener la respuesta impulso del sistema global e indicar a que tipo de sistema pertenece (FIR o IIR).
c. Comente acerca de la estabilidad interna y externa del sistema global. Justifique su respuesta.
d. Obtener la respuesta de paso del sistema global y determinar su valor cuando n→∞.
Coordinador: Tama Alberto
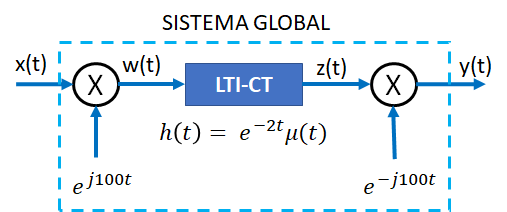
3Eva2016TII_T1 LTI CT con multiplicadores
3ra Evaluación II Término 2016-2017. 2/Marzo/2017. TELG1001
Tema 1. (24 puntos) Dominio de la frecuencia. Tal como se puede apreciar en la siguiente figura, un sistema LTI-CT ha sido integrado a formar parte de un Sistema Global, interconectándose a multiplicadores de señales complejas exponenciales, tanto a su entrada como a su salida.
a. Un estudiante de la materia Sistema Lineales, en el dominio del tiempo, ha demostrado que a pesar de los multiplicadores anteriormente especificados, el refereido Sistema Global sigue siendo LTI-CT. Determine entonces su respuesta impulso, es decir hequi(t) del Sistema Global.
b. El sistema global es ¿Con memoria o sin memoria?, ¿Causal o no causal?. ¿BIBO estable o no? Justifique sus respuestas de manera razonada.
c. Considere que el mismo estudiante, mencionado anteriormente, ha comprobado que dicho sistema global es invertible. Determinar entonces la respuesta impulso del sistema inverso, es decir hinv(t), misma que de acuerdo a la teoría nos permitirá obtener el denominado sistema identidad.
Coordinador: Tama Alberto