Publicado en

3Eva2014TI_T4 LTI DT h[n] subsistemas en serie, determinar a y b

3ra Evaluación I Término 2014-2015. 18/Septiembre/2014. TELG1001

Tema 4. (30 puntos) Dos sistema LTI-DT causales, tienen respuesta impulso h1[n] y h2[n] respectivamente.

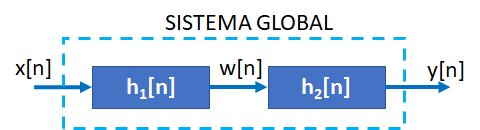
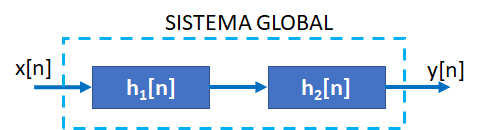
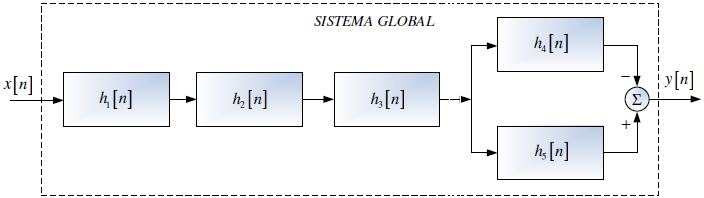
Los sistemas en referencia, utilizados como subsistemas, son conectados en cascada con la finalidad de conformar un sistema global, tal como se muestra en la siguiente figura.

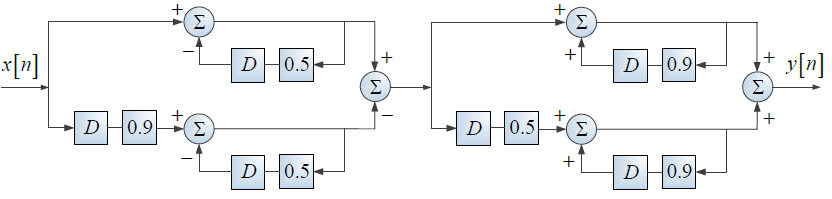
Las ecuaciones de diferencia que relacionan a cada sistema y al global, son las siguientes:

S1: w[n] = \frac{1}{2}w[n-1] +x[n] S2: y[n] = \alpha y[n-1] + \beta w[n] SG: y[n] = -\frac{1}{8}y[n-2] +\frac{3}{4} y[n-1]+ x [n]

Utilizando la transformada z:

a. Determinar los valores de α y β

b. Obtener la respuesta impulso del sistema global e indicar a qué tipo de sistema pertenece (FIR ó IIR).

c. Comente acerca de la estabilidad interna y exterma del sistema global. Justifique su respuesta.

d. Determinar y esquematizar la respuesta de paso del sistema global (SG).

Coordinador: Tama Alberto

Publicado en

3Eva2014TI_T3 LTI CT entrada compuesta

3ra Evaluación I Término 2014-2015. 18/Septiembre/2014. TELG1001

Tema 3. (30 puntos) Considere el sistema mostrado en la siguiente figura, donde la respuesta impulso h(t) está dada por:

h(t) = \frac{ \sin (11 \pi t)}{\pi t} x(t) = \sum_{k=1}^{\infty} \cos (5 k \pi t) g(t) = \sum_{k=1}^{10} \cos (8 k \pi t)

a. Determinar la energía contenida en la señal h(t).

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal m(t). Es decir M(ω) vs ω.

c. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal n(t). Es decir N(ω) vs ω.

d. Determinar la potencia de la señal de salida y(t) y la representación de su espectro de las Series de Fourier complejas exponenciales. Indique también el orden de los armónicos que están presentes en dicha salida.

Coordinador: Tama Alberto

Publicado en

3Eva2014TI_T2 LTI CT entrada modulada

3ra Evaluación I Término 2014-2015. 18/Septiembre/2014. TELG1001

Tema 2. (35 puntos) Considerar la existencia del sistema mostrado en la siguiente figura, donde el espectro de Fourier de su respuesa impulso h(t) es H(ω) vs ω.

Determinar, esquematizar y etiquetar, según corresponda lo siguiente:

a. El espectro de Fourier de p(t), es decir P(ω) vs ω.

b. La expresión analítica de q(t), como una función de x(t).

c. El espectro de Fourier de q(t), es decir Q(ω) vs ω.

d. El espectro de Fourier de y(t), es decir Y(ω) vs ω.

e. La salida o respuesta de dicho sistema. es decir y(t) sin esquematizar, ni etiquetar.

Coordinador: Tama Alberto

Publicado en

3Eva2014TI_T1 LTI CT en paralelo

3ra Evaluación I Término 2014-2015. 18/Septiembre/2014. TELG1001

Tema 1. (35 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que la respuesta y1(t), qe genera el sistema 1 que se muestra a continuación, está dada por lo especificado en dicha figura.

x_1 (t) = \text {rect} (t) y_1 (t) = \Delta \Bigg( \frac{t-2}{2} \Bigg)

a. Determinar, esquematizar y etiquetar la respuesta impulso h1(t) del referido sistema.

Para el diseño del sistema 2 esquematizado en la figura a continuación, determinar, esquematizar y etiquetar:

p (t) = \text{rect} (t) q (t) = \text{rect} (t-4)

b. la respuesta impulso equivalente, ess decir h2(t) del referido sistema (indicado mediante línea de traza),

c. La salida frente a la excitación que se especifica en dicha realización.

Coordinador: Tama Alberto

Publicado en

3Eva2012TII_T2 LTI DT H[z] por subsistemas y respuesta estado cero

3ra Evaluación II Término 2012-2013. 14/Febrero/2013. TELG1001

Tema 2. (40 puntos) El sistema que se muestra en la siguiente figura, es el resultante de la combinación de dos subsistemas conectados en cascada.

Considerando que ambos subsistemas son causales, determinar.

a. Las respuestas impulso de cada subsistema y del sistema completo. Es decir h1[n], h2[n] y h[n].

b. Justificando su respuesta, indicar si el sistema es BIBO estable, FIR o IIR.

c. La respuesta de estado cero y[n], en la forma de mínima expresión, frente a la siguiente entrada:

x[n] = \delta [n] - 2 \delta [n-1] + (2)^{-n} \mu [n]

Coordinador: Tama Alberto

Publicado en

3Eva2012TII_T1 LTI CT respuesta impulso

3ra Evaluación II Término 2012-2013. 14/Febrero/2013. TELG1001

Tema 1. (40 puntos) Una señal de entrada x(t) es muestreada mediante la utilización de un tren de impulsos s(t). Su resultante z(t) es utilizada como la excitación de un sistema LTI-CT, cuya respuesta de frecuencia H(ω) está representada en la siguiente figura:

a. Condediendo el hecho que

s(t) = \sum_{k=-\infty}^{\infty} \delta (t-k/2)

determinar, esquematizar y etiquetar su representación mediante series de Fourier armónicas, es decir Ck vs k.

b. Determinar, esquematizar y etiquetar la transformada de Fourier de la señal z(t), es decir Z(ω).

c. Utilizando la inversa de la transformada de Fourier, determinar la respuesta impulso del precitado sistema LTI-CT, es decir h(t).

d. Obtener el valor de la energía de las señales x(t) y h(t), es decir Ex(t) y Eh(t).

e. Determinar, esquematizar y etiquetr la transformada de Fourier de la señal y(t), es decir Y(ω)-

f. Obtener la respuesta y(t) y la energía asociada Ey(t) del precitado sistema LTI-CT.

Coordinador: Tama Alberto

Publicado en

3Eva2012TI_T4 LTI CT distorción de audio (scrambler)

3ra Evaluación I Término 2012-2013. 13/Septiembre/2012. TELG1001

Tema 4. (25 puntos) El sistema mostrado en la siguiente figura, es utilizado para distorsionar las señales de audio (scrambler-scrambling).

La señal x(t) es la versión modulada de la señal de entrada m(t), la misma que es la entrada a un filtro ideal pasa bajo, cuyo ancho de banda es de 15 [kHz]. De igual manera, también se puede afirmar que la salida del filtro pasa bajo y(t) es la versión distrorsionada de la señal de entrada m(t).

a. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal x(t); es decir X(ω) vs ω.

b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal y(t); es decir Y(ω) vs ω.

c. Utilizando la inversa de la Transformada de Fourier, determinar, esquematizar y etiquetar la señal de salida y(t).

Coordinador: Tama Alberto

Publicado en

3Eva2012TI_T3 LTI CT X(ω) transformar a x(t)

3ra Evaluación I Término 2012-2013. 13/Septiembre/2012. TELG1001

Tema 3. (25 puntos) Para la representación espectral que se muestra a continuación, determinar:

a. La inversa de la transformada de Fourier de X(ω), es decir x(t).

b. La energía contenida en la señal x(t)

Coordinador: Tama Alberto

Publicado en

3Eva2012TI_T2 LTI DT h[n] con subsistemas en serie-paralelo

3ra Evaluación I Término 2012-2013. 13/Septiembre/2012. TELG1001

Tema 2. (25 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que el Sistema Global que muestra en la siguiente figura, es el resultante de la combinación de cinco subsistemas interconectados.

Dado que:

h_1 [n] = \delta [n] - a \delta[n-1] h_2 [n] = \Bigg( \frac{1}{2} \Bigg)^2 \mu[n] h_3 [n] = a \mu [n] h_4 [n] = (n-1) \mu [n] h_5 [n] = \delta [n] - n \mu [n-1] + \delta [n-2]

Determinar la respuesta impulso del Sistema Global

Coordinador: Tama Alberto