Curso con Python – TELG1037/TELG1001 – FIEC – ESPOL
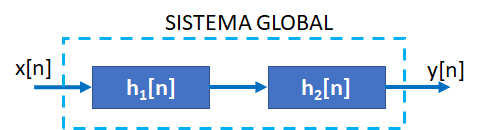
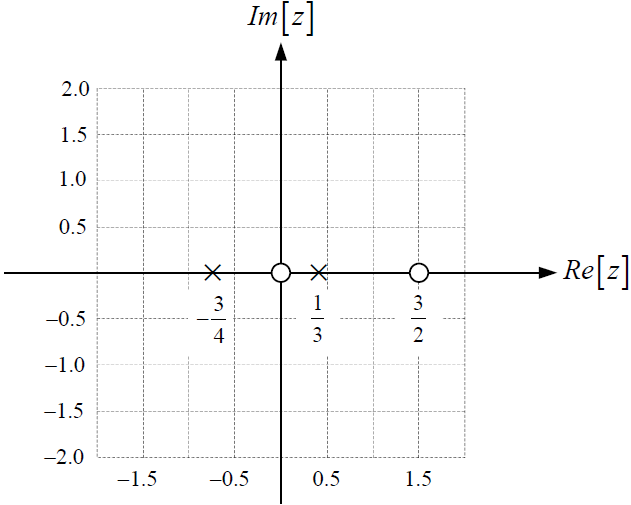
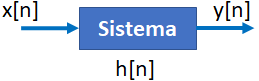
Tema 1. (25 puntos) Asumiendo causalidad para los sistemas en serie h1[n] y h2[n], se le solicita que mediante la utilización de la transformada z, determine la respuesta impulso h1[n], si se conoce y[n]:
a. La respuesta del segundo sistema está dada por:
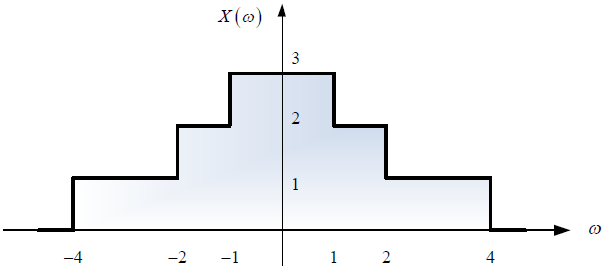
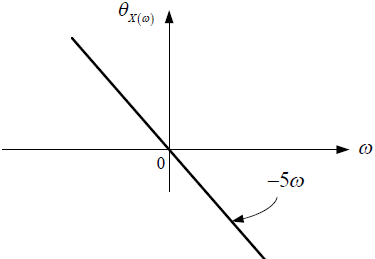
h_2 [n] = \delta[n] - \delta[n-1]b. Si dada la entrada x[n] se obtiene una salida y[n] esquematizada por:
x [n] = \mu [n] - \mu [n-2]Coordinador: Tama Alberto
Tema 3. (30 puntos) Para la representación espectral que se muestra a continuación, determinar:
a. La inversa de la transformada de Fourier de X(ω). Es decir x(t).
b. La energía contenida en la señal x(t).
Coordinador: Tama Alberto
Tema 2. (30 puntos) Las ubicaciones de polos y ceros para funciones H[z] se describen en el plano complejo z que se muestran en las siguientes figuras.
En cada caso identifique todas las ROC válidas para H[z], especificando las características (naturaleza) de la señal de tiempo h(n) correspondiente a cada ROC.
2.1. Gráfica para H1[z]
2.2. Gráfica para H2[z]
Tema 1. (40 puntos) Un estudiante de la materia Sistemas Lineales ha encontrado que la respuesta impulso h(t), de un sistema LTI-CT, es aquella que se especifica en la siguiente figura.
Si el referido sistema es excitado con la señal cuadrada periódica x(t), determinar, esquematizar y etiquetar según corresponda, lo siguiente:
a. La respuesta de frecuencia H(ω) vs ω.
b. La respuesta de frecuencia X(ω) vs ω.
c. La respuesta de frecuencia Y(ω) vs ω y Z(ω) vs ω.
d. La expresión analítica de la salida y(t).
Coordinador: Tama Alberto
Tema 3. (20 puntos) Considere el sistema mostrado en la siguiente figura:
a. Determinar la frecuencia angular fundamental w0 y el periodo fundamental T0 de la señal v(t)
b. Esquematizar y etiquetar el espectro de las Series de Fourier de la señal v(t).
c. Determinr la potencia de la señal v(t).
d. Obtener la señal de respuesta y(t) de dicho sistema.
Coordinador: Tama Alberto
Tema 2. (40 puntos) Considere la existencia del sistema global que es producto de la conexión en cascada de dos subsistemas, tal como se muestra en la siguiente figura:
Un estudiante de la materia Sistemas Lineales, ha determinado que la forma de la señal de salida v(t) es aquella que se esquematiza a continuación.
a. Obtener el valor que tomarían las constantes a, b, c.
b. Determinar la energía total contenida en la señal v(t).
c. Determinar, esquematizar y etiquetar la salida y(t) del sistema global y su energía total.
d. Dada la señal w(t), cuyo esquema se muestra anteriormente, expresar v(t) como una función de aquella.
e. Se conoce que la transformada de Fourier de la señal w(t) está dada por la siguiente expresión:
W(\omega) = \frac{1}{\omega^2} \Big( e^{j \omega} - j\omega e^{j\omega} -1 \Big)determine la transformada de Fourier de v(t).
Coordinador: Tama Alberto
Tema 1. (30 puntos) El sistema mostrado en la siguiente figura, es utilizado para distorsionar las señales de audio (scrambler-scrambling).
La señal x(t) es la versión modulada de la señal de entrada m(t), la misma que es la entrada a un filtro ideal pasa bajo, cuyo ancho de banda es de 15 [kHz]. De igual manera, también se puede afirmar que la salida del filtro pasa bajo y(t) es la versión distrorsionada de la señal de entrada m(t).
a. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal x(t); es decir X(ω) vs ω.
b. Determinar, esquematizar y etiquetar el espectro de Fourier de la señal y(t); es decir Y(ω) vs ω.
c. Utilizando la inversa de la Transformada de Fourier, determinar, esquematizar y etiquetar la señal de salida y(t).
Coordinador: Tama Alberto
Tema 4. (20 puntos) Para la representación espectral que se muestra a continuación, determinar:
a. La inversa de la transformada de Fourier de X(ω).
b. La energía contenida en la señal x(t).
Coordinador: Tama Alberto
Tema 3. (25 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que la ecuación de diferencias que relaciona la entrada-salida del LTI-DT causal, es aquella que se muestra en la siguiente figura.
y[n] – 1.6y[n-1] + 0.63 y[n-2] = 4 x[n-1] – 4 x[n-2]
Determinar:
a. La función de transferencia H(z) del mencionado sistema, esquematizando en el plan complejo sus polos y ceros.
b. El tipo de estabilidad (interna y externa) del sistema, justificando debidamente su respuesta.
c. La respuesta impulso h[n] del sistema.
d. La respuesta que generaría dicho sistema, si la excitación es una sinusoide muestreada cos(1500t) con un intervalo de muestreo de Ts= 0.0015.
e. El diagrama de bloques en su forma canónica (DFII) que representa la realización del referido sitema LTI-DT causal.
Referencia: 2Eva2010TI_T1 LTID Bloques de H[z] para ecuación de diferencias
Tema 2. (30 puntos) Considere el sistema LTI-CT, cuya respuesta al impulso unitario δ(t) es h(t), tal como se especifica en la siguiente figura.
Determinar, esquematizar y etiquetar según corresponda lo siguiente:
a. El espectro de Fourier de la señal g(t). Es decir G(ω) vs ω.
b. El espectro de Fourier de la respuesta impulso h(t). Es decir H(ω) vs ω.
c. El espectro de Fourier de la señal c(t). Es decir C(ω) vs ω.
d. El espectro de Fourier de la señal de salida y(t). Es decir Y(ω) vs ω.
Coordinador: Tama Alberto