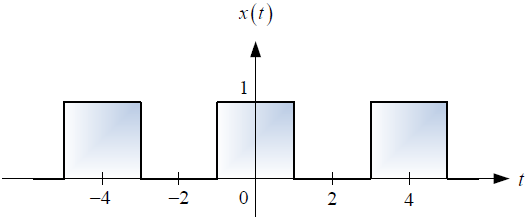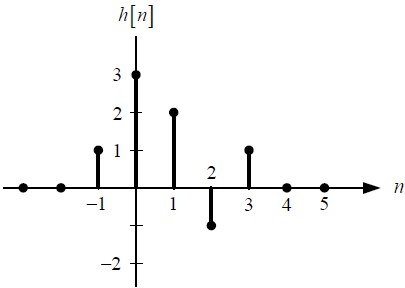3ra Evaluación II Término 2010-2011. 17/febrero/2011. TELG1001
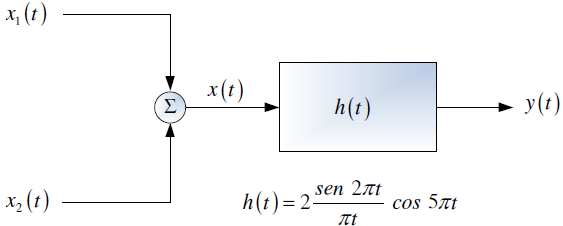
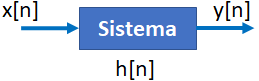
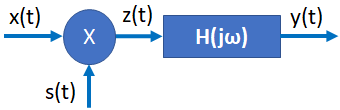
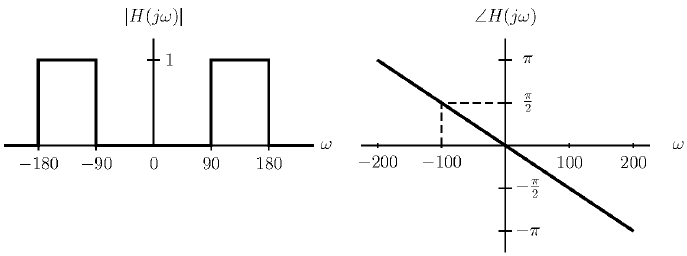
Tema 1. (25 puntos) Un estudiante de la materia Sistemas Lineales ha determinado que la respuesta a impulso h(t) de un sistema LTI-CT, es aquella que se especifica en la siguiente figura.
Si el referido sistema es excitado con la señal periódica x(t) cuya representación mediante coeficientes complejos de Fourier es:
Dk = j δ[k-1] – j δ[k+1] + δ[k-3] + δ[k+3]
ω0 = 2π
Determinar, esquematizar y etiquetar según corresponda lo siguiente:
a. La expresión analítica de la señal de entrada x(t) y su potencia.
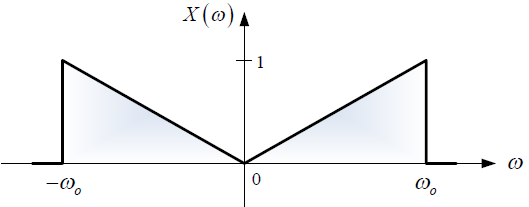
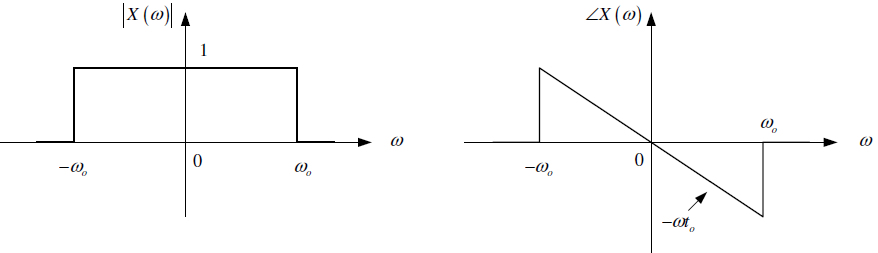
b. El espectro de Fourier de la señal de entrada x(t), esto es X(ω) vs ω.
c. El espectro de Fourier de la señal de entrada h(t), esto es H(ω) vs ω.
d. La expresión analítica de la salida y(t) y su potencia.
Coordinador: Tama Alberto