Autor: Edison Del Rosario

Ejercicio: 2Eva2016TII_T4 resolver en dominio de frecuencia

Partiendo de,

y(t) = x(t) \circledast h(t) Y(\omega) = X(\omega) H(\omega) Y\Big(\frac{\omega}{3}\Big) = X\Big(\frac{\omega}{3}\Big) H\Big(\frac{\omega}{3}\Big)

se tiene también que:

g(t) = x(3t) \circledast h(3t) G(\omega) = \frac{1}{3}X\Big(\frac{\omega}{3}\Big)\text{ } \frac{1}{3}H\Big(\frac{\omega}{3}\Big) = \frac{1}{9}X\Big(\frac{\omega}{3}\Big)H\Big(\frac{\omega}{3}\Big) = \frac{1}{9}Y\Big(\frac{\omega}{3}\Big) G(\omega) = \frac{1}{3} \Bigg[\frac{1}{3}Y\Big(\frac{\omega}{3}\Big)\Bigg] g(t) = \frac{1}{3} y(3t)

A = 1/3
B = 3

 

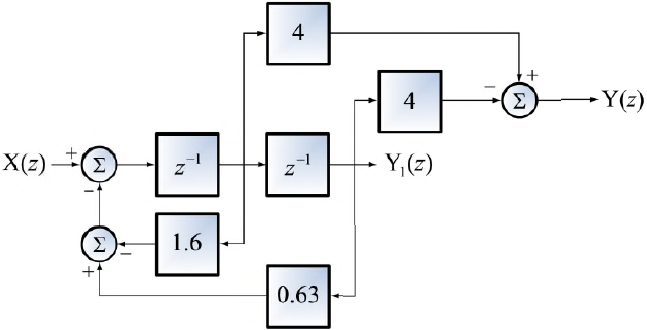
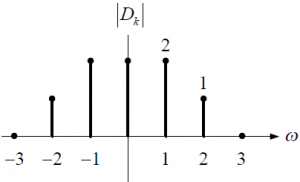
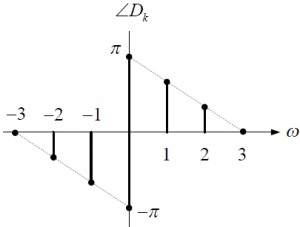
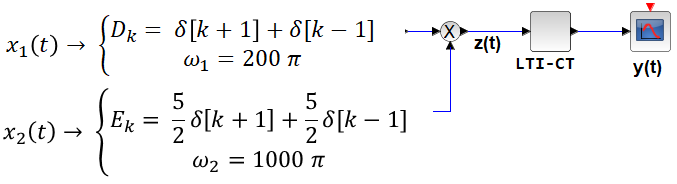Ejercicio: 2Eva2016TII_T3 LTI DT sistemas en serie

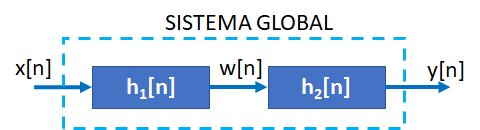
literal a

S1: w[n] = \frac{1}{2}w[n-1] + x[n] S2: y[n] = \alpha y[n-1] + \beta w[n] SG: y[n] = -\frac{1}{8}y[n-2] + \frac{3}{4}y[n-1]+x[n]

usando transformada z:

S1:

W(z) = \frac{1}{2} z^{-1} W(z) + X(z) W(z) - \frac{1}{2} z^{-1} W(z) = X(z) W(z)\Big[1 - \frac{1}{2} z^{-1} \Big] = X(z) W(z) = \frac{ X(z)}{\Big[1 - \frac{1}{2} z^{-1} \Big]}

S2:

Y(z) = \alpha z^{-1} Y(z) + \beta W(z) Y(z) - \alpha z^{-1} Y(z) = \beta W(z) Y(z) \Big[1 - \alpha z^{-1} \Big] = \beta W(z)

sustituyendo la ecuacion de S1 para W(z)

Y(z) \Big[1 - \alpha z^{-1} \Big] = \beta \frac{ X(z)}{\Big[1 - \frac{1}{2} z^{-1} \Big]} Y(z) \frac{1}{\beta} \Big[1 - \alpha z^{-1} \Big]\Big[1 - \frac{1}{2} z^{-1} \Big] = X(z) Y(z) \Big[ \frac{1}{\beta} - \frac{1/2+\alpha}{\beta} z^{-1}+ \frac{1}{2} \frac{\alpha}{\beta} z^{-2}\Big]= X(z)

SG:

Y(z) = -\frac{1}{8} z^{-2} Y(z) + \frac{3}{4} z^{-1}Y(z)+X(z) Y(z)+\frac{1}{8} z^{-2} Y(z) - \frac{3}{4} z^{-1}Y(z) = X(z) Y(z)\big[ 1 - \frac{3}{4} z^{-1} +\frac{1}{8} z^{-2} \Big] = X(z)

comparando con la ecuación de S2

\frac{1}{\beta} = 1 \beta = 1 \frac{1}{2} \frac{\alpha}{\beta} = \frac{1}{8} \alpha = \frac{2\beta}{8} = \frac{1}{4}

comprobar con

- \frac{1/2+\alpha}{\beta} = \frac{3}{4}

se confirma que  α = 1/4 y β=1

la función de transferencia es:

Y(z)\Big[ 1 - \frac{3}{4} z^{-1} +\frac{1}{8} z^{-2} \Big] = X(z) \frac{Y(z)}{X(z)} = \frac{1}{\Big[ 1 - \frac{3}{4} z^{-1} +\frac{1}{8} z^{-2} \Big]} H(z) = \frac{z^2}{z^2 - \frac{3}{4} z +\frac{1}{8}} \frac{H(z)}{z} = \frac{z}{z^2 - \frac{3}{4} z +\frac{1}{8}}

usando las raices para:

z^2 - \frac{3}{4} z +\frac{1}{8} = \Big[ z-\frac{1}{4}\Big] \Big[z-\frac{1}{2}\Big]

y la parte derecha de la ecuación:

\frac{z}{\Big[ z-\frac{1}{4}\Big] \Big[z-\frac{1}{2}\Big]} = \frac{C_1}{z-\frac{1}{4}}+\frac{C_2}{z-\frac{1}{2}}

despejando para C1 y haciendo z=1/4,

C_1 = \frac{z}{\Big[z-\frac{1}{2}\Big]} = \frac{\frac{1}{4}}{\Big[\frac{1}{4}-\frac{1}{2}\Big]} = -1

despejando para C2 y haciendo z=1/2,

C_2 = \frac{z}{\Big[z-\frac{1}{4}\Big]} = \frac{\frac{1}{2}}{\Big[\frac{1}{2}-\frac{1}{4}\Big]} = 2

se H(z) se resume en,

H(z) = - \frac{z}{z - \frac{1}{4}} +2\frac{z}{z-\frac{1}{2}}

Para obtener h[n] usando la antitransformada,

h[n]=z^{-1} \Big[ H(z) \Big] h[n]=z^{-1} \Big[- \frac{z}{z - \frac{1}{4}} +2\frac{z}{z-\frac{1}{2}} \Big] h[n]= 2 \Big[ \frac{1}{2}\Big]^n \mu [n] + \Big[ \frac{1}{4}\Big]^n \mu [n] h[n]= \Bigg[ 2 \Big[ \frac{1}{2}\Big]^n - \Big[ \frac{1}{4}\Big]^n \Bigg] \mu [n]

siendo la forma de la respuesta un impulso, es un sistema IIR.

---

Algoritmo en Python

Usando la expresión H(z) se obtiene:

 Hz:
      2     
     z      
------------
 2   3*z   1
z  - --- + -
      4    8

 Hz en fracciones parciales
     z        2*z  
- ------- + -------
  z - 1/4   z - 1/2

 Hz en factores
          2         
         z          
--------------------
(z - 0.5)*(z - 0.25)

 {Q_polos:veces}: {1/2: 1, 1/4: 1}
 {P_ceros:veces}: {0: 2}

estabilidad asintótica en z:
circ1_dentro : 2
circ1_repetidos : 0
circ1_sobre : 0
circ1_fuera : 0
unicos : 2
repetidos : 0
asintota : estable

 h[n]:
/      n        n\             
\- 0.25  + 2*0.5 /*Heaviside(n)
>>> 

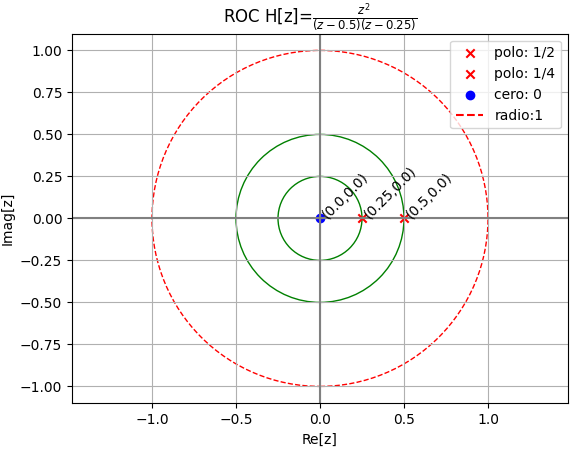
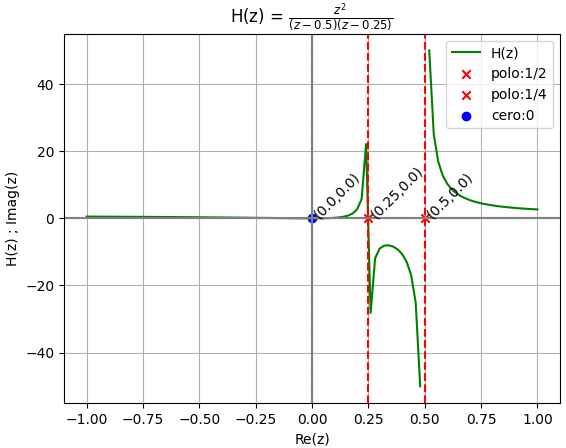
añadiendo instrucciones para graficar h[n] se obtiene

señal discreta h[n]
n   : [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]
h[n]: [1.         0.75       0.4375     0.234375   0.12109375
       0.06152344 0.03100586 0.01556396 0.00779724 0.00390244]

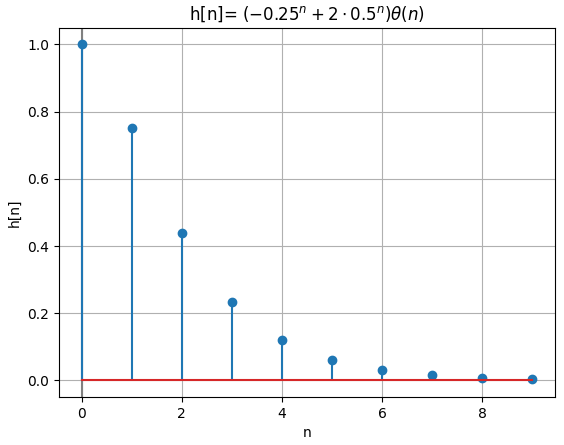
Instrucciones en Python

strong>Nota: cuando se produzca el siguiente error con Numpy para evaluar una expresión con exponente negativo,

Traceback (most recent call last):
  File "D:\MATG1052Ejemplos\Transformadaz\ejercicio....py", line 93, in 
    fi  = f_n(ki)
  File "", line 2, in _lambdifygenerated
    return (9/59)*4**(-n)*Heaviside(n, 1/2)
ValueError: Integers to negative integer powers are not allowed.

proceda actualizando los valores a evaluar como tipo real (dtype float), tan solo usando en la línea de ki con lo siguiente:

ki  = np.arange(0,muestras_fn,1.0)

quedando las instrucciones de la siguiente forma, que si evalua valores para realizar gráficas.

# Transformada z- Fracciones parciales
# http://blog.espol.edu.ec/telg1001/lti-dt-transformada-z-xz-fracciones-parciales-con-python/
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
import telg1001 as fcnm
#sym.SYMPY_DEBUG=True

# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n', real=True)

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(3,4)
a1 = sym.Rational(1,8)

Pz = z**2
Qz = z**2-a0*z+a1

#Pz = z*z**2
#Qz = (z-1)*(z**2-(a0)*z+a1)

F = Pz/Qz

# para graficar
f_nombre = 'H'    # nombre de función[z]: H,X,Y, etc
muestras_fn = 10  # muestras para f[n]

# PROCEDIMIENTO
Fz  = fcnm.apart_z(F)
Fz_factor = sym.factor(F.evalf())
Fz_factor = fcnm._round_float_is_int(Fz_factor)

# polos y ceros de Hz
[P,Q] = Fz.as_numer_denom()
P = sym.poly(P,z)
Q = sym.poly(Q,z)
P_ceros = sym.roots(P)
Q_polos = sym.roots(Q)

estable_z = fcnm.estabilidad_asintotica_z(Q_polos)

# Inversa de transformada z
fn = 0*n ; Fz_revisar = [] ; Qz2_term =[]
term_sum = sym.Add.make_args(Fz)
for term_k in term_sum:
    term_kn = fcnm.inverse_z_transform(term_k,z,n)
    if type(term_kn)==tuple:
        fn = fn + term_kn[0]
    elif term_kn is not None:
        fn = fn + term_kn
    elif term_kn is None:
        f_noeval = f_noeval + term_k
    Qz2 = fcnm.Q_cuad_z_parametros(term_k)
    if Qz2:
        Qz2_term.append(Qz2)
fn = fn.collect(sym.Heaviside(n))
fn = fn.collect(sym.DiracDelta(n))
fn = fcnm._round_float_is_int(fn)

# SALIDA
print('\n '+f_nombre+'z:')
sym.pprint(F)
print('\n '+f_nombre+'z en fracciones parciales')
sym.pprint(Fz)
print('\n '+f_nombre+'z en factores')
sym.pprint(Fz_factor)
print('\n {Q_polos:veces}:',Q_polos)
print(' {P_ceros:veces}:',P_ceros)
if len(Qz2_term)>0:
    print('\nparametros cuadraticos: ')
    for i in range(0,len(Qz2_term),1):
        for unterm in Qz2_term[i]:
            print(' termino:',unterm)
            fcnm.print_resultado_dict(Qz2_term[i][unterm])
print('\nestabilidad asintótica en z:')
fcnm.print_resultado_dict(estable_z)
print('\n '+f_nombre.lower()+'[n]:')
sym.pprint(fn)
if len(Fz_revisar)>0:
    print('revisar terminos sin transformada de tabla:')
    for un_term in Fz_revisar:
        print(un_term)

# # GRAFICA  -----------
fig_ROC = fcnm.graficar_Fz_polos(Fz_factor,Q_polos,P_ceros,
                      muestras=101,f_nombre=f_nombre)

fig_Fz = fcnm.graficar_Fs(Fz_factor,Q_polos,P_ceros,
                     muestras=101,
                     f_nombre=f_nombre)

# graficar f[n] -------
f_n = sym.lambdify(n,fn.expand(),modules=fcnm.equivalentes)
ki  = np.arange(0,muestras_fn,1.0)
fi  = f_n(ki)

print('\nseñal discreta '+f_nombre.lower()+'[n]')
print('n   :',ki)
print(f_nombre.lower()+'[n]:',fi)

# graficar f[n]
fig_fn, grafxn = plt.subplots()
plt.axvline(0,color='grey')
plt.stem(ki,fi)
plt.grid()
plt.xlabel('n')
plt.ylabel(f_nombre.lower()+'[n]')
etiqueta = r''+f_nombre.lower()+'[n]= $'+str(sym.latex(fn))+'$'
plt.title(etiqueta)

plt.show()

 

---

Literal c

revisando los polos y ceros:

ceros : z = 0  y z = 0
polos: z=1/4 y z=1/2

Dado que todos los polos se encuentran dentro del círculo de radio unitario , el sistema es asintóticamente estable, por lo que es BIBO o EASA estable

literal d

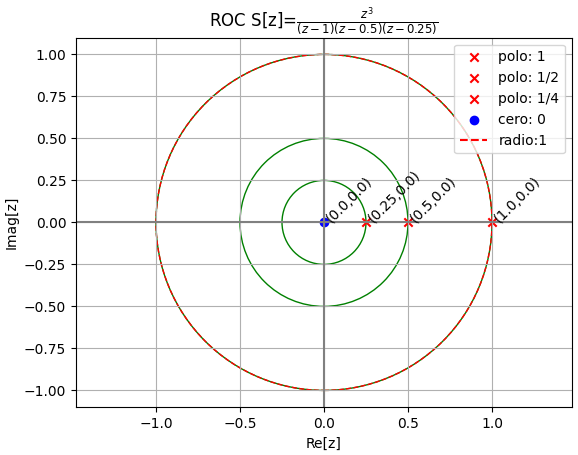
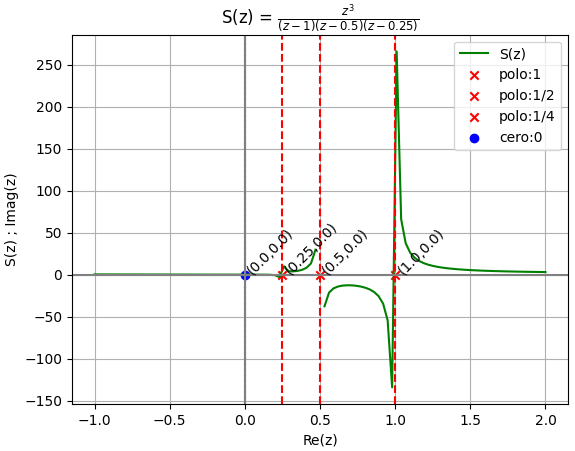
S(z) = \Big[ \frac{z}{z-1} \Big] \frac{z^2}{z^2-\frac{3}{4}z + \frac{1}{8}} S(z) = \frac{z^3}{(z-1)(z-1/4)(z-1/2)}

aplicando el mismo método anterior, se tiene:

# coeficientes como racional en dominio 'ZZ' enteros
a0 = sym.Rational(3.4)
a1 = sym.Rational(1,8)

Pz = z*z**2
Qz = (z-1)*(z**2-(a0)*z+a1)
F = Pz/Qz

# para graficar
f_nombre = 'S'    # nombre de función[z]: H,X,Y, etc
muestras_fn = 10  # muestras para f[n]

con resultado:

 Sz:
           3          
          z           
----------------------
        / 2   3*z   1\
(z - 1)*|z  - --- + -|
        \      4    8/

 Sz en fracciones parciales
     z          2*z        8*z   
----------- - ------- + ---------
3*(z - 1/4)   z - 1/2   3*(z - 1)

 Sz en factores
              3             
             z              
----------------------------
(z - 1)*(z - 0.5)*(z - 0.25)

 {Q_polos:veces}: {1: 1, 1/2: 1, 1/4: 1}
 {P_ceros:veces}: {0: 3}

 s[n]:
/    n             \             
|0.25         n   8|             
|----- - 2*0.5  + -|*Heaviside(n)
\  3              3/             

S(z) = \frac{1}{3}\frac{z}{z-1/4} -2\frac{z}{z-1/2} + \frac{8}{3}\frac{z}{z-1}

aplicando la transformada inversa

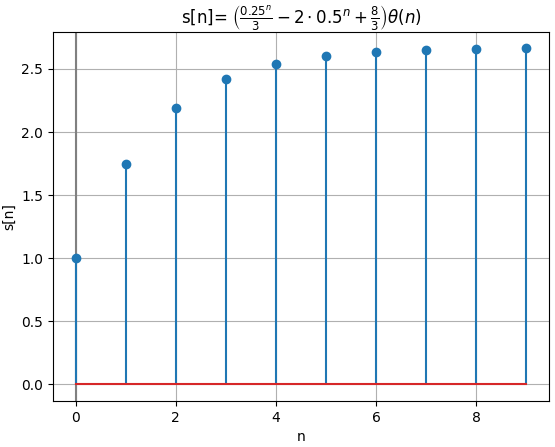
s(n)= \Bigg[ \frac{1}{3}\Big[ \frac{1}{4} \Big]^n -2\Big[\frac{1}{2} \Big]^n + \frac{8}{3} \Bigg] \mu [n]

señal discreta s[n]
n   : [0 1 2 3 4 5 6 7 8 9]
h[n]: [1.         1.75       2.1875     2.421875   
 2.54296875 2.60449219 2.63549805 2.65106201 2.65885925
 2.66276169]

 

Ejercicio: 2Eva2016TII_T2 LTI CT Circuito RC respuesta de frecuencia H(ω), impulso h(t)

literal a

v_1 (t) = v_R (t) +v_C (t) v_1 (t) = R i(t) +v_2 (t) i(t) = C \frac{\delta v_2 (t)}{\delta t} v_2(t) = RC \frac{\delta v_2 (t)}{\delta t} +v_2 (t) V_1 (\omega) = j \omega RC V_2 (\omega) + V_2(\omega) = V_2(\omega) [1+j\omega RC] H(\omega) = \frac{V_2 (\omega)}{V_1(\omega)} = \frac{1}{1+j\omega RC} = \frac{1}{1+j\frac{\omega}{\omega_c}} \omega _c = \frac{1}{RC} H(\omega) =\frac{V_2(\omega)}{V_1(\omega)} = \frac{1}{1+j\frac{\omega}{2}} \begin{cases} |H(\omega) = \frac{1}{\sqrt{1+\big( \frac{\omega}{2}\big)^2}} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{\omega}{2}\big) \end{cases} \omega _c = \frac{1}{RC}

literal c

La respuesta impulso del filtro LPF, se obtiene mediante:

h(t) = \mathcal{F}^{-1} \Big[ H(\omega) \Big] = \mathcal{F}^{-1} \Big[ \frac{1}{1+j(\omega /2)} \Big] =2\mathcal{F}^{-1} \Big[ \frac{1}{j\omega +2} \Big] h(t)=2e^{2t}\mu (t)

literal d

Método 1: usando la respuesta de frecuencia

\begin{cases} |H(\omega) = \frac{1}{\sqrt{1+\big( \frac{\omega}{2}\big)^2}} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{\omega}{2}\big) \end{cases} \begin{cases} |H(50) = \frac{1}{\sqrt{1+\big( \frac{50}{2}\big)^2}} = \frac{1}{\sqrt(626)} \\ \theta_{H(\omega)} = -tg^{-1} \big( \frac{50}{2}\big) = -87.7\end{cases} v_2(t) = |H(50)| \sin \big(50t+\theta_{H(50)} \big) v_2(t) = \frac{1}{\sqrt(626)} \sin \big(50t-87.7) \big)

método 2:

V_2(\omega ) = V_1(\omega) H(\omega) V_1 (\omega) = \mathcal{F}[v_1(t) ] = \mathcal{F} [ \sin (50t) ] = j \pi \delta (\omega +50) - j \pi \delta (\omega-50) V_2 (\omega) = V_1(\omega) H(\omega) V_2 (\omega) = \Big[ j \pi \delta (\omega +50) - j \pi \delta (\omega-50) \Big] \Big[ \frac{1}{1+j(\omega/2)} \Big] = j \pi \Big[ \delta (\omega + 50)\frac{1}{1+j(\omega /2)} - \delta (\omega - 50)\frac{1}{1+j(\omega /2)}\Big] = j \pi \Big[ \delta (\omega + 50)\frac{1}{1+j(50 /2)} - \delta (\omega - 50)\frac{1}{1+j(50 /2)}\Big] = j \pi \Big[ \delta (\omega + 50)\frac{1+j25}{626} - \delta (\omega - 50)\frac{1-j25}{626}\Big] = j \frac{\pi}{626} \Big[ \delta (\omega + 50) - \delta (\omega - 50) + j25 \delta (\omega + 50) + j25 \delta (\omega - 50)\Big] = \frac{1}{626} \Big[ j\pi \delta (\omega + 50) - j \pi \delta(\omega - 50)\Big] - \frac{25}{626} \Big[ \pi \delta (\omega + 50) +\pi \delta(\omega - 50)\Big] v_2(t) = \mathcal{F}^{-1} [V_2 (\omega)] = \frac{1}{626} \mathcal{F}^{-1}\Bigg[ \Big[ j\pi \delta (\omega + 50) - j \pi \delta(\omega - 50)\Big] - 25 \Big[ \pi \delta (\omega + 50) +\pi \delta(\omega - 50)\Big] \Bigg] v_2(t) = \frac{1}{626} \Big[ \sin (50t) - 25 \cos (50t) \Big]

usando fasores:

v_2(t) = \frac{1}{626} \cos (50t-177.709) = \frac{1}{626} \sin (50t-87.70)

En la salida, existe un factor de atenuación de 0.04 y un retardo de 87.70°.
Como la señal de entrada se reproduce de manera exacta en su salida a pesar tener amplitud diferente y un retardo en el tiempo.