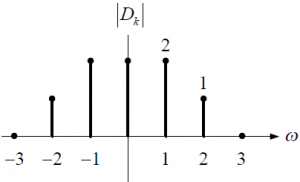
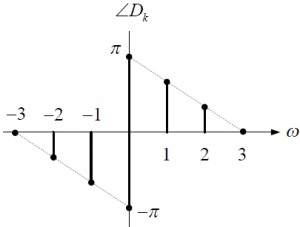
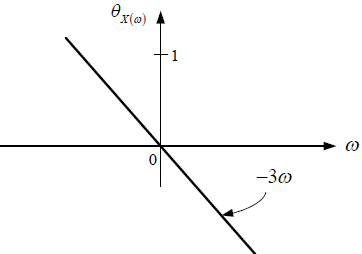2da Evaluación II Término 2012-2013. 31/Enero/2013. TELG1001
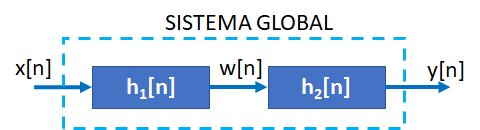
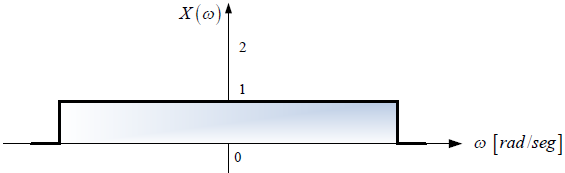
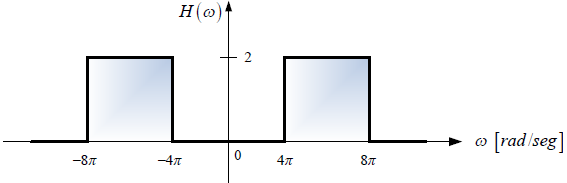
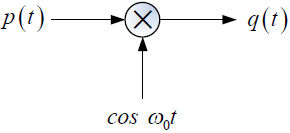
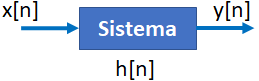
Tema 3. (35 puntos) Considerar la existencia del sistema mostrado en la siguiente figura, donde el espectro de Fourier de la respuesta impulso h(t) es H(ω).

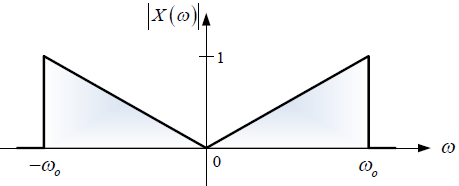
a. Determinar, esquematizar y etiquetar el espectro de Fourier de x(t), es decir X(ω) vs ω.
b. Determinar la expresión analítica de q(t), como una función de x(t).
c. Determinar, esquematizar y etiquetar los espectros de Fourier de las señales g(t), p(t) y q(t), es decir G(ω), P(ω) y Q(ω) respectivamente.
d. Determinar, esquematizar y etiquetar el espectro de Fourier de y(t), es decir Y(ω) vs ω.
e. Expresar la salida y(t) como una función de x(t).
f. Hallar la energía de la señal de salida y(t), es decir Ey(t).
Coordinador: Tama Alberto