Referencia: Lathi 4.5 p386, Oppenheim 9.8.2 p708,
Representaciones en diagramas de bloques para los sistemas LTI causales descritos por ecuaciones diferenciales y en el dominio s por funciones racionales H(s). Los diagramas se desarrollan con software abierto como Xcos de SciLab.
[H(s) 1er orden] [H(s) 2do orden combinado de 1er orden] [H(s) 2do Orden componentes Serie o Paralelo]
Ejemplo 1. H(s) Diagrama de bloques y sistema de 1er orden
Referencia: Oppenheim ejemplo 9.28 p708, Lathi ejemplo 4.22a p392
Considere un sistema LTI causal 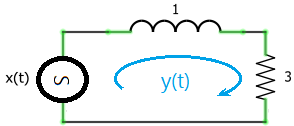
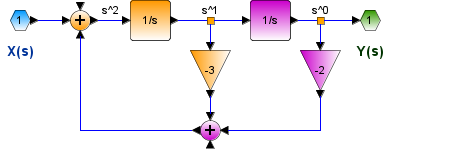
Se presenta un bloque integrador (1/s) de la señal de entrada X(s) con retroalimentación de salida Y(s).
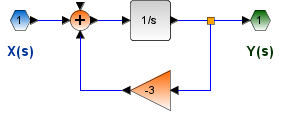 Agrupando Y(s) para obtener polinomios de s
Agrupando Y(s) para obtener polinomios de s
Se puede expresar la relación como una función de transferencia H(s):
H(s)= \frac{Y(s)}{X(s)} =\frac{1}{s+3}Otra forma de expresar H(s), al mutiplicar el numerador y denominador por 1/s
que confirma que, para dos bloques H1(s) = 1/s y H2(s) = 3, interconectados en el diagrama, se tiene:
\frac{Y(s)}{X(s)} = H(s) = \frac{H_1(s)}{1+H_1(s)H_2(s)}[H(s) 1er orden] [H(s) 2do orden combinado de 1er orden] [H(s) 2do Orden componentes Serie o Paralelo]
Ejemplo 2. H(s) Diagrama de bloques de sistema de 2do orden como combinación de 1er orden.
Referencia: Oppenheim ejemplo 9.30 p711, Lathi 4.5-3 p393
Considere el sistema causal de segundo orden con la función del sistema:
H(s) = \frac{1}{(s+1)(s+2)} = \frac{1}{s^2 + 3s +2}Para la ecuación diferencial se usa la forma,
H(s) = \frac{Y(s)}{X(s)} = \frac{1}{s^2 + 3s +2} (s^2 + 3s + 2)Y(s) = X(s) s^2 Y(s) + 3sY(s) + 2Y(s) = X(s)la entrada x(t) y la salida y(t) para este sistema satisfacen la ecuación diferencial:
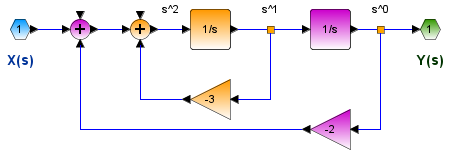
\frac{\delta^2}{\delta t^2}y(t) + 3 \frac{\delta}{dt} y(t) + 2 y(t) = x(t)El diagrama de bloques se obtiene reordenando la ecuación de s para despejar el término de mayor grado.
s^2Y(s) = X(s) - 3sY(s) - 2Y(s) Y(s) = \frac{1}{s^2} \Big[ X(s) - 3sY(s) - 2Y(s)\Big]reordenando los bloques:
Ejemplo 2.1 Reordenando expresión de H(s) con fracciones parciales
Usando H(s) de la primera expresión del enunciado, se usa fracciones parciales para reordenar la expresión como:
H(s) = \frac{1}{(s+1)(s+2)} = \frac{k_1}{s+1} + \frac{k_2}{s+2}Para encontrar las constantes k1 y k2, el numerador de la expresión de la derecha debe ser igual a 1 , desarrollando la expresión para el numerador se tiene que:
k_1s + 2k_1 + k_2s + k_2 = (k_1 + k_2)s + (2k_1 +k_2)igualando al numerador de la parte izquierda que es 1, o expresado como 0s+1, el resultado debería ser:
(k_1 + k_2)s + (2k_1 +k_2) = 0s + 1Se crean las ecuaciones para cada coeficiente de s en el numerador:
k_1 + k_2 = 0 2k_1 + k_2 = 1con lo que,
k_1 = 1 , k_2 = -1al reemplazar,
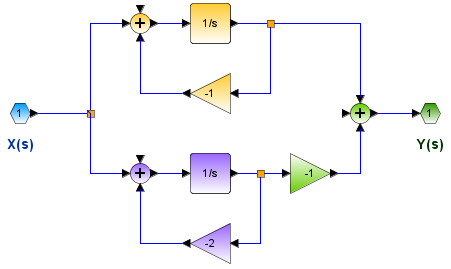
H(s) = \frac{1}{s+1} -\frac{1}{s+2}El resultado permite realizar un diagrama equivalente en paralelo de dos sistemas mas simples. La suma de dos componentes de primer orden es un diagrama con bloques de primer orden en paralelo.
En el caso de la expresión racional inicial, se observa que se puede escribir como la multiplicación de dos sistemas de primer orden.
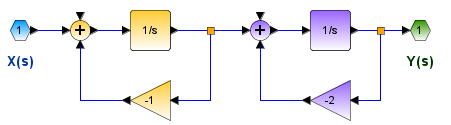
H(s) = \frac{1}{(s+1)(s+2)} = \Big[\frac{1}{s+1}\Big]\Big[\frac{1}{s+2}\Big]que se representa como bloques en serie o cascada de dos sistemas de primer orden.
que por cierto, también es la convolución de dos sistemas en serie.
Ejemplo 2.2 Resolviendo fracciones parciales usando Sympy-Python
También es posible realizar las fracciones parciales con Sympy ingresando toda la expresión de H(s) de la forma:
Hs = 1/((s+1)*(s+2))
y usando sym.apart() se obtienen las fracciones parciales de la expresión,
H(s):
1
---------------
(s + 1)*(s + 2)
H(s) en fracciones parciales:
1 1
- ----- + -----
s + 2 s + 1
>>>
las instrucciones en Sympy-Python a ser usadas son:
# Fracciones parciales con Laplace # Ps es numerador, Qs es denominador # Oppenheim 9.30 p711 import sympy as sym # INGRESO s = sym.Symbol('s') Hs = 1/((s+1)*(s+2)) # PROCEDIMIENTO # fracciones parciales de s Hs_parcial = sym.apart(Hs,s) # SALIDA print('H(s):') sym.pprint(Hs) print('\n H(s) en fracciones parciales:') sym.pprint(Hs_parcial)
La instruccion sym.apart() se aplica sobre expresiones tipo polinomio, se debe considerar el caso cuando H(s) es solo un componente constante o tiene un desplazamiento de tiempo representado por sym.exp(). El asunto se trata en la siguiente página sobre fracciones parciales.
[H(s) 1er orden] [H(s) 2do orden combinado de 1er orden] [H(s) 2do Orden componentes Serie o Paralelo]
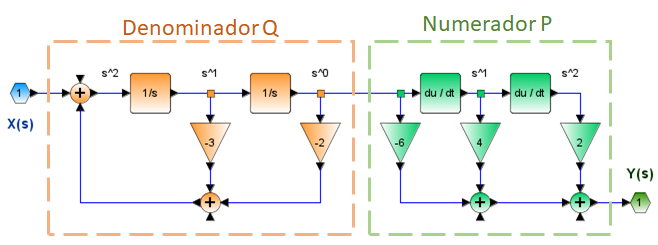
Ejemplo 3. H(s) Diagrama de bloques de sistema 2do orden componentes en serie o paralelo
Referencia: Oppenheim ejemplo 9.31.p712/pdf743, Lathi Ejemplo 4.23 p395
Considere la función del sistema
H(s) = \frac{2s^2 + 4s - 6}{s^2 + 3s + 2}se puede reescribir como:
H(s) = \Big[\frac{1}{s^2 + 3s + 2} \Big] \Big[ 2s^2 + 4s - 6 \Big]Para los componentes del numerador P pueden tomar respuestas del bloque denominador Q simplificando el diagrama :
Ejemplo 3.1 H(s) con fracciones parciales
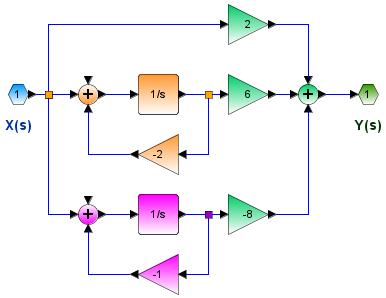
Usando fracciones parciales, se puede convertir H(s) en componentes mas simples en paralelo
H(s) = 2 + \frac{6}{s+2} - \frac{8}{s+1}Usando las raíces del numerador P se escribe H(s) de la forma en que se obtiene un sistema en serie o cascada,
H(s) = \Big[ 2\Big] \Big[\frac{s-1}{s+2} \Big] \Big[\frac{s+3}{s+1} \Big]Ejemplo 3.2 Fracciones parciales usando Sympy
H(s):
2
2*s + 4*s - 6
--------------
2
s + 3*s + 2
H(s) en fracciones parciales:
6 8
2 + ----- - -----
s + 2 s + 1
H(s) como factores:
2*(s - 1)*(s + 3)
-----------------
(s + 1)*(s + 2)
H(s) simplificada:
/ 2 \
2*\s + 2*s - 3/
----------------
2
s + 3*s + 2
# Fracciones parciales con Laplace, factores # Ps es numerador, Qs es denominador # Oppenheim 9.30 p711 import sympy as sym # INGRESO s = sym.Symbol('s') Ps = 2*s**2+4*s-6 Qs = s**2+3*s+2 Hs = Ps/Qs # PROCEDIMIENTO # fracciones parciales de s Hs_parcial = sym.apart(Hs,s) # expresion con factores de s Hs_factor = sym.factor(Hs_parcial,s) # simplificar a la forma inicial Hs_simple = sym.simplify(Hs_parcial) # SALIDA print('H(s):') sym.pprint(Hs) print('\n H(s) en fracciones parciales:') sym.pprint(Hs_parcial) print('\n H(s) como factores:') sym.pprint(Hs_factor) print('\n H(s) simplificada:') sym.pprint(Hs_simple)
La instrucción sym.factor() aplica sobre expresiones simples. En caso de disponer la expresión como polinomica, puede usar la conversión con Hs_parcial.as_expr(s).
Ejemplo 3.3 Ecuación diferencial de H(s)
H(s) = \frac{Y(s)}{X(s)} = \frac{2s^2 + 4s - 6}{s^2 + 3s + 2}Se reordena la expresión,
(s^2 + 3s + 2)Y(s) = (2s^2 + 4s - 6) X(s) s^2 Y(s) +3s Y(s) + 2Y(s) = 2 s^2 X(s) + 4s X(s) - 6X(s)Si considera la forma de la ecuación diferencial, tambien es la de un circuito eléctrico RLC. El primer término Y(t) sería el del inductor L, pero expresado como primera derivada. El segundo término es el resistor y el tercer término es del capacitor. Lo que se puede apreciar dividiendo toda la ecuación para ‘s’.
sY(s) +3 Y(s) + 2\frac{1}{s}Y(s) = 2 s X(s) + 4 X(s) - 6\frac{1}{s}X(s)que es el circuito de los primeros ejemplos de Sistema – Modelo entrada-salida.
Sustituyendo las s de Laplace por derivadas y Y(s) por y(t) en la expresión de 2do orden,
\frac{\delta ^2}{\delta t^2} y(t) + 3\frac{\delta}{\delta t} y(t) + 2y(t) = 2\frac{\delta ^2}{\delta t^2} x(t) + 4\frac{\delta}{\delta t} x(t) - 6x(t)En las próximas secciones se analiza la estabilidad del sistema para las señales de salida usando polos y ceros.