Referencia: Lathi ejemplo 4 p330, Hsu literal C. p112
La función de transferencia H(s) se escribe como P(s)/Q(s) que es una expresión racional de s. Se considera que en la expresión el grado m del polinomio del numerador P(s) es mayor que el grado n del polinomio del denominador Q(s). Las raíces del polinomio P(s) del numerador se conocen como ceros, pues convierten la expresión en cero, mientras que para el denominador las raices se denominan polos al convertir en infinito la expresión (Hsu).
\frac{P(s)}{Q(s)} = \frac{a_0(s-ceros(1))\text{...}(s-ceros(m))}{b_0(s - polos(1)) \text{...} (s - polos(n))}otra forma de escribir los polos y ceros (Lathi)
\frac{P(s)}{Q(s)} = \frac{ceros(1)}{s - polos(1)}+\frac{ceros(2)}{s - polos(2)}+\text{ ... } \text{ ... }+\frac{ceros(n)}{s - polos(n)}+ganancia(s)Para el desarrollo de un algoritmo con Sympy, el primer paso consiste en determinan los polos de un ejercicio.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo, busca_polosceros(Hs) ]
Ejemplo 1. Polos reales no repetidos y fracciones parciales
Referencia: Hsu problema 3.17a p137, Lathi ejemplo 4.3a p338, Oppenheim ejemplo 9.9 p671
La expresión H(s) tiene los componentes de P(s) y Q(s) como se indican,
H(s) = \frac{2s+4}{s^2 +4s+3}Ingreso de H(s) como P(s) y Q(s)
Para la expresión de la función de transferencia, con Sympy se crean los polinomios del numerador Ps y denominador Qs.
# INGRESO s = sym.Symbol('s') Ps = 2*s + 4 # 1+0*s cuando es constante Qs = s**2 + 4*s + 3 Hs = Ps/Qs
Siendo H(s) la forma en que se expresan los ejercicios, se realizan las operaciones para obtener las raíces del numerador y denominador. El resultado buscado con el algoritmo es:
H(s):
2*(s + 2)
---------------
(s + 1)*(s + 3)
H(s) en fracciones parciales
1 1
----- + -----
s + 3 s + 1
{Q_polos:veces}: {-1: 1, -3: 1}
{P_ceros:veces}: {-2: 1}
>>>
Instrucciones en Python
Hs se convierte en una expresión de Sympy con sym.sympify(Hs)s para el caso en que se de tan solo una constante. En el caso que Hs requiera agrupar términos se usa la instrucción sym.simplify(Hs,inverse=True).
Una vez preparada la expresión Hs, se separa como numerador Ps y denominador Qs en forma de polinomio para obtener las raíces y las veces que ocurren con la instrucción sym.roots().
La expresión de H(s) en fracciones parciales se obtienen usando sym.apart(Hs,s).
# Busca Polos y Ceros de H(s) con Sympy # Ps es numerador, Qs es denominador import sympy as sym # INGRESO s = sym.Symbol('s') Ps = 2*s + 4 Qs = s**2 + 4*s + 3 Hs = Ps/Qs # PROCEDIMIENTO Hs = sym.sympify(Hs) # convierte a sympy una constante Hs = sym.simplify(Hs,inverse=True) # agrupa terminos # polos y ceros de Hs [P,Q] = Hs.as_numer_denom() P = P.as_poly(s) # numerador Q = Q.as_poly(s) # denominador P_ceros = sym.roots(P) Q_polos = sym.roots(Q) # en factores Hs = sym.factor(Hs,s) # fracciones parciales Hs_fp = sym.apart(Hs,s) # SALIDA print('H(s):') sym.pprint(Hs) print('\n H(s) en fracciones parciales ') sym.pprint(Hs_fp) print('\n {Q_polos:veces}:',Q_polos) print('\n {P_ceros:veces}:',P_ceros)
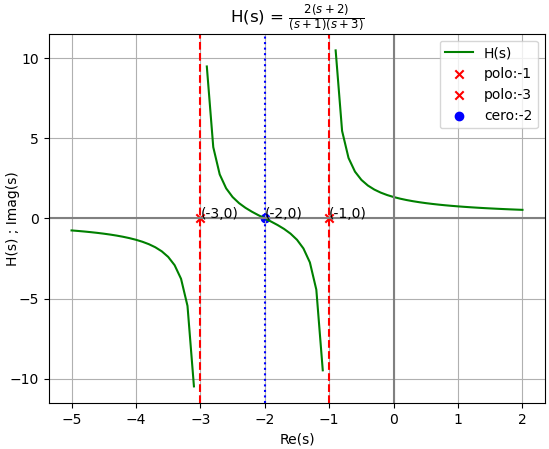
Para visualizar el concepto de polos y ceros, se presenta la gráfica de polos y ceros en el dominio s, para un corte en el plano real. Por simplicidad se usará el procedimiento creado para el curso en telg1001.py
Todos los polos y ceros se encuentran en el lado izquierdo del plano, es decir su parte real es negativa.
# GRAFICA ----------- import matplotlib.pyplot as plt import telg1001 as fcnm fig_Hs = fcnm.graficar_Fs(Hs,Q_polos,P_ceros,f_nombre='H') plt.show()
Para revisar los polos de la expresión de fracciones parciales, se considera que los términos de las expresiones podrían tener polos repetidos como en el ejemplo 3. Para polos repetidos, se usa el número de veces mayor cuando aparecen polos de términos suma.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 2. Grados iguales de P(s) y Q(s), ceros con valores complejos
Referencia: Lathi ejemplo 4.3b p338, Hsu ejercicio 3.20 p140, Oppenheim ejemplo 9.36 p716
H(s) = \frac{2s^2 +5}{s^2 +3s+2}Ejemplo 2 Desarrollo con Sympy-Python
Al algoritmo del ejercicio anterior se modifica solo el bloque de ingreso con las expresiones para numerador y denominador:
Ps = 2*s**2+5 Qs = s**2 + 3*s + 2 Hs = Ps/Qs
El resultado Hs_fp en fracciones parciales muestra que existe un término constante en las sumas de la expresión. La forma descrita por Lathi al inicio de la página, la constante se la considera como ‘ganancia(s)’.
H(s):
2
2*s + 5
---------------
(s + 1)*(s + 2)
H(s) en fracciones parciales
13 7
2 - ----- + -----
s + 2 s + 1
{Q_polos:veces}: {-1: 1, -2: 1}
{P_ceros:veces}: {-sqrt(10)*I/2: 1, sqrt(10)*I/2: 1}
>>>
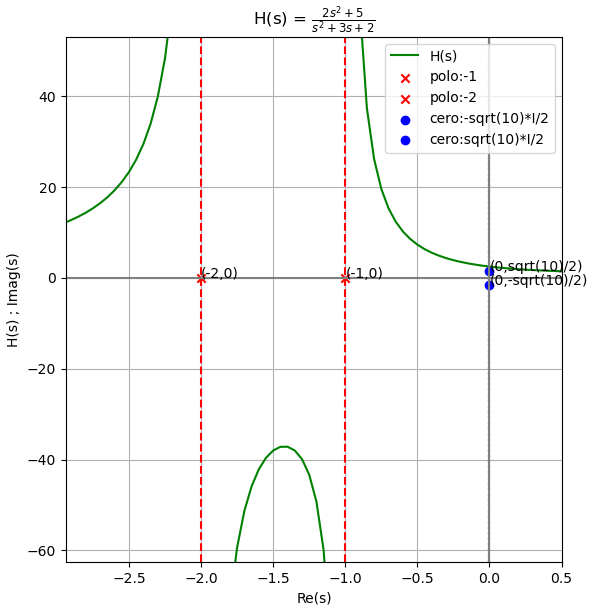
Por otra parte se tiene que los ceros tienen raíces con componente imaginario representado con el símbolo ‘I‘, que para representar cada raíz en la gráfica se considera el eje vertical también como parte Imag(s). Si es cierto, es diferente a la naturaleza de H(s), perdonen, se usa ésta «libertad» solo para resaltar la influencia de los polos en H(s) como se mostró en el ejercicio anterior, o se realizaría un gráfico con el plano real e imaginario como base y una tercera dimensión para H(s).
Los polos se encuentran en el lado izquierdo del plano, es decir su parte real es negativa.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 3. Polos reales repetidos o raices repetidas en denominador Q(s)
Referencia: Lathi ejemplo 4.3d p342
H(s) = \frac{8s+10}{(s+1)(s+2)^3}la forma de la expresión para el algoritmo es
Ps = 8*s+10 Qs = (s+1)*((s+2)**3) Hs = Ps/Qs
En él ejercicio el término del denominador tiene un factor elevado al cubo, lo que muestra que la raiz es repetida y se debe reflejar en la respuesta del algoritmo. En las fracciones parciales se muestra que para el polo repetido existe un término suma para cada grado en el denominador.
H(s):
2*(4*s + 5)
----------------
3
(s + 1)*(s + 2)
H(s) en fracciones parciales
2 2 6 2
- ----- - -------- + -------- + -----
s + 2 2 3 s + 1
(s + 2) (s + 2)
{Q_polos:veces}: {-1: 1, -2: 3}
{P_ceros:veces}: {-5/4: 1}
>>>
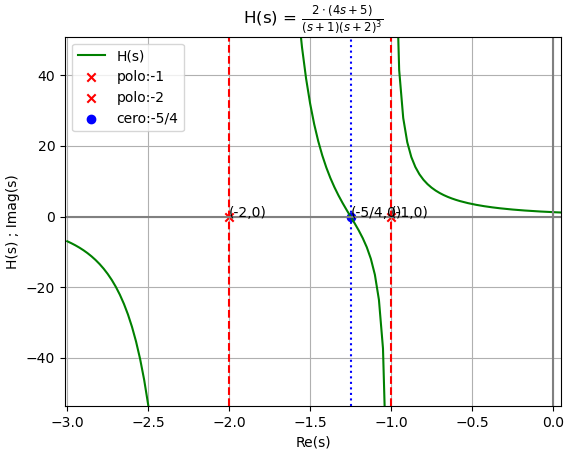
Todos los polos y ceros se encuentran en el lado izquierdo del plano s.
Se adjunta la gráfica para la interpretación de H(s)
Si la busqueda de polos es sobre la expresión de fracciones parciales, se tiene que las veces se determinan como el mayor exponente del término del denominador.
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 4. H(s) con Fracciones parciales y polos de tipo complejo
Referencia: Lathi ejemplo 4.3c p340
H(s) = \frac{6(s+34)}{s(s^2+10s+34)}la forma de la expresión para el algoritmo es
Ps = 6*(s+34) Qs = s*(s**2+10*s+34) Hs = Ps/Qs
Incorporando las instrucciones para identificar si el denominador tiene raices complejas, se asignan los valores de los parametros necesarios en un diccionario de variables, obteniendo como resultado,
H(s):
6*(s + 34)
------------------
/ 2 \
s*\s + 10*s + 34/
H(s) en fracciones parciales
6*(s + 9) 6
- -------------- + -
2 s
s + 10*s + 34
{Q_polos:veces}: {-5 - 3*I: 1, -5 + 3*I: 1, 0: 1}
{P_ceros:veces}: {-34: 1}
h(t):
-5*t
- 2*(4*sin(3*t) + 3*cos(3*t))*e *Heaviside(t) + 6*Heaviside(t)
>>>
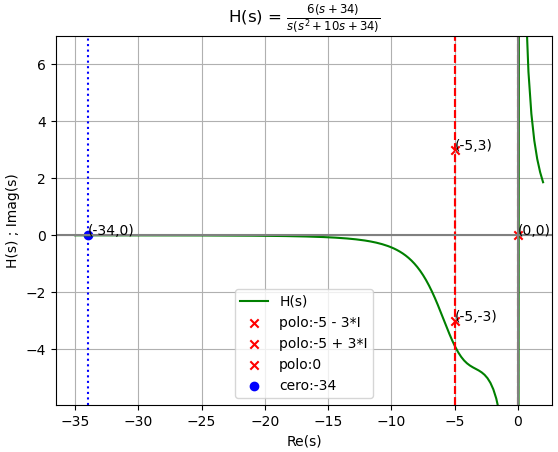
grafica ejemplo 4
Ejemplo 4 Instrucciones en Python
# Fracciones parciales de H(s) con Sympy # Ps es numerador, Qs es denominador # con Transformada Inversa de Laplace import numpy as np import sympy as sym # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) Ps = 6*(s+34) Qs = s*(s**2+10*s+34) Hs = Ps/Qs # PROCEDIMIENTO Hs = sym.simplify(Hs,inverse=True) # Hs debería ser un solo termino suma Hs = sym.factor(Hs,s) # fracciones parciales Hsp = sym.apart(Hs,s) # Analiza polos def polosceros_simple(Hs): ''' Busca_polo de un termino sin exp(-a*s) ''' Hs = sym.simplify(Hs,inverse=True) # Hs debería ser un solo termino suma Hs_factor = sym.factor(Hs,s) # polos y ceros de termino Hs [P,Q] = Hs_factor.as_numer_denom() P = sym.poly(P,s) # numerador Q = sym.poly(Q,s) # denominador P_ceros = sym.roots(P) Q_polos = sym.roots(Q) respuesta = {'Q_polos' : Q_polos, 'P_ceros' : P_ceros} return(respuesta) polosceros = polosceros_simple(Hs) # SALIDA print('H(s):') sym.pprint(Hs) print('\n H(s) en fracciones parciales ') sym.pprint(Hsp) print('\n {Q_polos:veces}:',polosceros['Q_polos']) print(' {P_ceros:veces}:',polosceros['P_ceros']) print('\n h(t): ') sym.pprint(ht)
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]
Ejemplo 5. Con suma de términos y exponenciales de retraso en tiempo
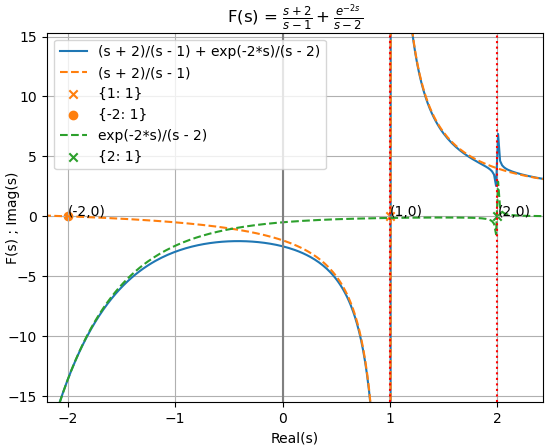
H(s) = \frac{s+2}{s-1}+ \frac{e^{-2s}}{s-2}la expresión para el algoritmo se escribe como:
Hs = ((s+2)/(s-1)) + sym.exp(-2*s)/(s-2)
Para el segundo término que tiene un exponencial, no se puede aplicar directamente la instrucción sym.apart(Hs,s) al no ser reconocida como tipo polinomio. Para continuar se debe separar el término sym.exp() del resto de la expresión, y se podrá aplicar fracciones parciales a esa parte, para luego volver a poner el término.
Para facilitar el desarrollo del algoritmo, se recomienda empezar a analizar una expresión mas simple, como solamente el segundo término de la suma.
expresion H(s):
-2*s
s + 2 e
----- + -----
s - 1 s - 2
Polos y ceros:
término: 1 * (s + 2)/(s - 1)
Q_polos{polos:veces}: {1: 1}
P_ceros{polos:veces}: {-2: 1}
término: exp(-2*s) * 1/(s - 2)
Q_polos{polos:veces}: {2: 1}
P_ceros{polos:veces}: {}
>>>
En el algoritmo se empieza por determinar si la expresión de Hs tiene términos sym.exp(-s), la instrucción que permite listar estos términos es
lista_exp = list(Hs.atoms(sym.exp(-s)))
como la expresión H(s) en los ejercicios puede contener sumas o multiplicaciones de bloques, primero se simplifica la expresión H(s)
# convierte a Sympy si es solo constante Hs = sym.sympify(Hs) # simplifica operación Hs1(s)*Hs2(s) Hs = sym.expand_power_exp(Hs) Hs = sym.expand(Hs, power_exp=False) term_sum = sym.Add.make_args(Hs) Hs_0 = 0*s # reagrupa Fs for term_k in term_sum: term_k = sym.simplify(term_k) term_k = sym.expand_power_exp(term_k) Hs_0 = Hs_0 + term_k # tabula sym.exp(-s) en lista_exp lista_exp = list(Hs_0.atoms(sym.exp(-s))) if len(lista_exp)>0: # elimina constantes for k in lista_exp: if not(k.has(s)): # es constante lista_exp.remove(k)
luego se tabula la lista_exp y se eliminan los términos que pueden ser constantes o no dependen de ‘s’, por ejemplo sym.exp(10).
Luego se separa la expresión por grupos usando sym.collect() creando un diccionario con los elementos de la lista_exp y con las expresiones agrupadas.
# separados por lista_exp separados = sym.collect(Hs_0,lista_exp,evaluate=False)
Con los elementos separados se puede aplicar la búsqueda de polos y ceros para cada elemento de la lista con la función polosceros_simple(Hs_k)
Al final se pueden agrupar los Q_polos y P_ceros de toda la expresión siguiendo criterios como que las veces que ocurre cada polo es el maximo entre los términos separados por lista_exp.
Instrucciones en Python
# Busca Polos y Ceros de H(s) con Sympy # separa términos con sym.exp(-a*s) # Ps es numerador, Qs es denominador import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') # Ps = (2*s + 4) # Qs = s**2 + 4*s + 3 # Ps = 2*s**2+5 # Qs = s**2 + 3*s + 2 # Ps = 8*s+10 # Qs = (s+1)*((s+2)**3) # Ps = 6*(s+34) # Qs = s*(s**2+10*s+34) # Hs = Ps/Qs # Hs = sym.exp(-2*s)/(s-2) # Hs = 1/s - sym.exp(-2*s)/s # Hs = sym.exp(-2*s)/s -sym.exp(-4*s)/s # Hs = (2*s**2+5*s+12)/((s+2)*(s**2+2*s+10)) Hs = ((s+2)/(s-1)) + sym.exp(-2*s)/(s-2) # PROCEDIMIENTO def busca_polosceros(Hs): ''' Busca polos de Hs (divisiones para cero) y ceros de Hs,cuenta las veces que aparecen, agrupa por exp(-a*s) agrupado en factores. ''' def polosceros_simple(Hs): ''' Busca_polo de un termino sin exp(-a*s) ''' Hs = sym.simplify(Hs,inverse=True) # Hs debería ser un solo termino suma Hs_factor = sym.factor(Hs,s) # polos y ceros de termino Hs [P,Q] = Hs_factor.as_numer_denom() P = sym.poly(P,s) # numerador Q = sym.poly(Q,s) # denominador P_ceros = sym.roots(P) Q_polos = sym.roots(Q) respuesta = {'Q_polos' : Q_polos, 'P_ceros' : P_ceros} return(respuesta) # convierte a Sympy si es solo constante Hs = sym.sympify(Hs) # simplifica operación Hs1(s)*Hs2(s) Hs = sym.expand_power_exp(Hs) Hs = sym.expand(Hs, power_exp=False) term_sum = sym.Add.make_args(Hs) Hs_0 = 0*s # reagrupa Fs for term_k in term_sum: term_k = sym.simplify(term_k) term_k = sym.expand_power_exp(term_k) Hs_0 = Hs_0 + term_k # tabula sym.exp(-s) en lista_exp lista_exp = list(Hs_0.atoms(sym.exp(-s))) if len(lista_exp)>0: # elimina constantes for k in lista_exp: if not(k.has(s)): # es constante lista_exp.remove(k) # separados por lista_exp separados = sym.collect(Hs_0,lista_exp,evaluate=False) # polos y ceros por terminos exp(-s) agrupados polosceros = {} ; Hs_fp = 0 for k in separados: Hs_k = sym.factor(separados[k],s) PZ_k = polosceros_simple(Hs_k) PZ_k['Hs_k'] = Hs_k polosceros[k] = PZ_k # integra polos Q_polos = {} ; P_ceros = {} for k in polosceros: polos = polosceros[k]['Q_polos'] for unpolo in polos: if unpolo in Q_polos: veces = max([Q_polos[unpolo],polos[unpolo]]) Q_polos[unpolo] = veces else: Q_polos[unpolo] = polos[unpolo] ceros = polosceros[k]['P_ceros'] for uncero in ceros: if uncero in P_ceros: veces = max([P_ceros[uncero],ceros[uncero]]) P_ceros[unpolo] = veces else: P_ceros[uncero] = ceros[uncero] # revisa exp(-a*s) if len(lista_exp)==0: #sin componentes del polosceros['1'] polosceros['Q_polos'] = Q_polos polosceros['P_ceros'] = P_ceros return(polosceros) polosceros = busca_polosceros(Hs) # SALIDA print('\n expresion H(s):') sym.pprint(Hs) print('\nPolos y ceros:') lista_PZ = ['Q_polos','P_ceros'] for k in polosceros: if not(k in lista_PZ): print('término:', k,'*',polosceros[k]['Hs_k']) print(' Q_polos{polos:veces}: ',polosceros[k]['Q_polos']) print(' P_ceros{polos:veces}: ',polosceros[k]['P_ceros']) else: print(k,polosceros[k])
La gráfica en éste caso se realiza usando Hs y sus componentes, de ésta forma es posible visualizar el efeto de cada componente con sus polos y ceros.
# GRAFICA ---------------------- def graficar_Fs2(Fs,Q_polos={},P_ceros={}, s_a=1,s_b=0,muestras=101,f_nombre='F', solopolos=False,polosceros={}): # grafica Fs lista_Hs =[] lista_PZ = ['Q_polos','P_ceros'] lista_term = list(polosceros.keys()) lista_term.remove('Q_polos') lista_term.remove('P_ceros') # intervalo para s,y componentes Fs con exp(-a*s) s_a = 0 ; s_b = 0 ; Lista_Hs = [] cond_componente = False if len(lista_term)>0: cond_componente = True if len(polosceros)>1: # tiene componenes con exp(-a*s) lista_Hs.append([Hs,{},{}]) for k in polosceros: if not(k in lista_PZ): Q_polosk = polosceros[k]['Q_polos'] P_cerosk = polosceros[k]['P_ceros'] [s_ak,s_bk] = fcnm.intervalo_s(Q_polosk,P_cerosk) s_a = min(s_a,s_ak) s_b = max(s_b,s_bk) lista_Hs.append([polosceros[k]['Hs_k']*sym.sympify(k), Q_polosk,P_cerosk]) else: #sin componenes con exp(-a*s) lista_Hs.append([Hs,polosceros['Q_polos'],polosceros['P_ceros']]) [s_a,s_b] = fcnm.intervalo_s(polosceros['Q_polos'], polosceros['P_ceros']) # graficas por cada componente fig_Fs, graf_Fs = plt.subplots() # no presenta errores de división para cero en lambdify() np.seterr(divide='ignore', invalid='ignore') for k in lista_Hs: Fs_k = k[0] ;Q_polosk = k[1] ;P_cerosk = k[2] # convierte a sympy una constante Fs_k = sym.sympify(Fs_k,s) if Fs_k.has(s): # no es constante F_s = sym.lambdify(s,Fs_k,modules=fcnm.equivalentes) else: F_s = lambda s: Fs_k + 0*s s_i = np.linspace(s_a,s_b,muestras) Fsi = F_s(s_i) # Revisar cuando s es complejo lineaestilo = 'solid' if len(Q_polosk)>0 and cond_componente: lineaestilo = 'dashed' graf_Fs.plot(s_i,Fsi,label=Fs_k,linestyle=lineaestilo) lineacolor = plt.gca().lines[-1].get_color() if len(Q_polosk)>0: polo_re = [] ; polo_im = [] for polos in Q_polosk.keys(): graf_Fs.axvline(sym.re(polos),color='red', linestyle='dotted') x_polo = sym.re(polos) y_polo = sym.im(polos) polo_re.append(x_polo) polo_im.append(y_polo) etiqueta = "("+str(x_polo)+','+str(y_polo)+")" graf_Fs.annotate(etiqueta,(x_polo,y_polo)) graf_Fs.scatter(polo_re,polo_im,marker='x', color =lineacolor, label = Q_polosk) if len(P_cerosk)>0: cero_re = [] ; cero_im = [] for cero in P_cerosk.keys(): x_cero = sym.re(cero) y_cero = sym.im(cero) cero_re.append(x_cero) cero_im.append(y_cero) etiqueta = "("+str(x_cero)+','+str(y_cero)+")" graf_Fs.annotate(etiqueta,(x_cero,y_cero)) graf_Fs.scatter(cero_re,cero_im,marker='o', color =lineacolor, label = P_cerosk) graf_Fs.axvline(0,color='gray') graf_Fs.legend() graf_Fs.set_xlabel('Real(s)') graf_Fs.set_ylabel('F(s) ; Imag(s)') graf_Fs.set_title(r'F(s) = $'+str(sym.latex(Hs))+'$') graf_Fs.grid() return(fig_Fs) fig_Fs = graficar_Fs2(Hs,polosceros=polosceros) plt.show()
Parametros cuadráticos
Para el ejercicio 4, se tienen polos con valores complejos y para usar la tabla de transformadas de Laplace se requiere obtener algunos parámetros.
Referencia: Lathi ejemplo 4.3c p340
H(s) = \frac{6(s+34)}{s(s^2+10s+34)}el desarrollo se puede describir como
H(s) = \frac{6(s+34)}{s(s^2+10s+34)} = \frac{k_1}{s} + \frac{As+B}{s^2+10s+34}usando el método de Heaviside, se obtiene k1
k_1 = \frac{6(s+34)}{\cancel{s}(s^2+10s+34)}\Big|_{s=0} =\frac{6(0+34)}{(0^2+10(0)+34)} = \frac{6(34)}{34}=6 \frac{6(s+34)}{s(s^2+10s+34)} = \frac{6}{s} + \frac{As+B}{s^2+10s+34}se simplifican las fracciones al multiplicar ambos lados por s(s2+10s+34)
6(s+34) = 6(s^2+10s+34) + (As+B)s 6s+204 = 6s^2+60s+204 + A s^2+Bs 6s+204 = (6+A)s^2+(60+B)s+204se puede observar que 6+A=0, por lo que A=-6.
Tambien se tiene que 60+B=6, por lo que B=-54
quedando la expresión como:
Observando la tabla de transformadas de Laplace se compara la expresión con las filas 12c y 12d se usan los parametros de:
\frac{As+B}{s^2+2as+c}A= -6, B=-64, a=5, c = 34
y se calculan:
con lo que se puede escribir la transformada inversa de Laplace para h(t) como
h(t) = [6+10e^{-5t}\cos (3t--0.9272)] \mu (t)o la otra foma de expresión usando la fila 12d de la tabla
Ejemplo 4 Desarrollo con Sympy-Python
Incorporando las instrucciones para identificar si el denominador tiene raices complejas, se asignan los valores de los parámetros necesarios en un diccionario de variables, obteniendo como resultado,
H(s) en fracciones parciales:
6*(s + 9) 6
- -------------- + -
2 s
s + 10*s + 34
parametros de Q_cuadratico:
-6*(s + 9)/(s**2 + 10*s + 34) :
{'A': -6.0, 'B': -54.0, 'a': 5.0, 'c': 34.0, 'r': 10.0, 'b': 3.0, 'theta': -0.9272952180016122}
>>>
mientras que el algoritmo se resume en
# Fracciones parciales de H(s) con Sympy # Ps es numerador, Qs es denominador # con Transformada Inversa de Laplace import numpy as np import sympy as sym import telg1001 as fcnm # INGRESO s = sym.Symbol('s') t = sym.Symbol('t', real=True) Ps = 6*(s+34) Qs = s*(s**2+10*s+34) Hs = Ps/Qs # PROCEDIMIENTO # parametros de termino con Q cuadratico def Q_cuad_s_parametros(Hs): '''Si Q tiene grado=2, obtiene los parametros para la tabla de Transformadas Inversas de Laplace ''' def Q_cuad_sin_exp(Hs): '''para Hs sin sym.exp(-a*s) ''' # fracciones parciales NO separa Q con factores complejos Hs_fp = sym.apart(Hs,s) respuesta = {} term_suma = sym.Add.make_args(Hs_fp) for term_k in term_suma: [P,Q] = term_k.as_numer_denom() if sym.degree(Q) == 2 and sym.degree(P) == 1: P_coef = P.as_coefficients_dict(s) Q_coef = Q.as_coefficients_dict(s) Q0 = 1 # Normalizar coefficiente s**2=1 if Q_coef[s**2]!=1: Q0 = Q_coef[s**2] # Parametros de Q cuadratico a = 0 ; c = 0 if s**1 in Q_coef: a = float(Q_coef[s**1]/Q0)/2 if s**0 in Q_coef: c = float(Q_coef[s**0]/Q0) A = float(P_coef[s**1]) B = 0 if s**0 in P_coef: B = float(P_coef[s**0]) rP = (A**2)*c + B**2 - 2*A*B*a rQ = c - a**2 r = np.sqrt(rP/rQ) b = np.sqrt(c-a**2) thetaP = A*a-B thetaQ = A*np.sqrt(c-a**2) theta = np.arctan(thetaP/thetaQ) parametro = {'A': A, 'B': B,'a': a, 'c': c, 'r': r, 'b': b,'theta':theta} respuesta[term_k] = parametro return (respuesta) Hs = sym.sympify(Hs,s) Hs_fp = fcnm.apart_s(Hs) # separa por sym.exp(-a*s) # tabula sym.exp(-s) en lista_exp lista_exp = list(Hs_fp.atoms(sym.exp(-s))) if len(lista_exp)>0: # elimina constantes for k in lista_exp: if not(k.has(s)): # es constante lista_exp.remove(k) # separados por lista_exp separados = sym.collect(Hs_fp,lista_exp,evaluate=False) Qs2 = {} # agrupa parametros Qs2 for k in separados: Qs2_k = Q_cuad_sin_exp(separados[k]) if len(Qs2_k)>0: for term in Qs2_k: Qs2[k*term] = Qs2_k[term] return(Qs2) Hs_fp = fcnm.apart_s(Hs) Qs2 = Q_cuad_s_parametros(Hs) # SALIDA print('H(s) en fracciones parciales:') sym.pprint(Hs_fp) # parametros de termino con Q cuadratico if len(Qs2)>0: print('\n parametros de Q_cuadratico: ') for k in Qs2: print(' ',k,' :') print(' ',Qs2[k])
[ polos reales no repetidos ] [ grados iguales P y Q ] [ polos reales repetidos ] [polos complejos ] [ con exponencial s o retraso en tiempo ]