Sympy ofrece la instrucción sym.laplace_transform(ft,t,s) para expresiones de f(t) con términos simples. La instrucción desarrolla el integral unilateral con t entre [0,∞], es decir con entradas tipo causal con t>0 o con términos μ(t) y los desplazados hacia la derecha μ(t-1).
Partiendo de las variable ‘t‘ y ‘s‘ como símbolos , se establece la expresión correspondiente en f(t) para determinar F(s). La transformada se obtiene al usar la instrucción:
Fs_L = sym.laplace_transform(ft,t,s)
Fs = Fs_L[0] # solo expresion
El resultado contiene la expresión, el valor de un polo del plano de convergencia y una condición de convergencia auxiliar. Para los objetivos de los ejercicios el enfoque es sobre el primer componente Fs = Fs_L[0].
En los ejercicios desarrollados se describen las ventajas y restricciones al usar las instrucciones librería Sympy, versión 1.11.1 o superior al 2022.10.30. Se indica que el inconveniente está resuelto en la versión 1.12 22/11/2022 https://github.com/sympy/sympy/issues/24294
Por simplicidad, el análisis de polos y ceros se realiza en la sección de estabilidad del sistema con Python
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]
Ejemplo 1. Transformada de Laplace de una exponencial decreciente, un solo termino
Referencia: Lathi ejemplo 4.1. p331, Oppenheim Ejemplo 9.2 p656, Hsu Ejemplo 3.1 p111
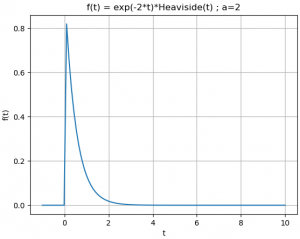
Para una señal f(t),
se tiene la transformada F(s),
F(s) = \frac{1}{s+a}realizar la transformada con la instrucción directa de Sympy:
Siendo las variables t, u de tipo símbolo, se definen las funciones como,
u = sym.Heaviside(t) ft = sym.exp(-a*t)*u
el resultado de la operación será:
f(t): -a*t e *Heaviside(t) F(s): 1 ----- a + s
Se puede verificar el resultado en la Tabla de Transformadas de Laplace
Instrucciones con Python para Ejemplo 1
# Transformadas de Laplace Unilateral con Sympy # supone f(t) causal, usa escalón u(t) import sympy as sym # INGRESO t = sym.Symbol('t', real=True) a = sym.Symbol('a', real=True) s = sym.Symbol('s') u = sym.Heaviside(t) ft = sym.exp(-a*t)*u # PROCEDIMIENTO ft = sym.expand(ft,t) # términos de suma Fs_L = sym.laplace_transform(ft,t,s) Fs = Fs_L[0] # solo expresion # SALIDA print('\n f(t): ') sym.pprint(ft) print('\n F(s): ') sym.pprint(Fs)
Realizado el primer ejemplo con las instrucciones Sympy, se obtiene una guia para continuar con otros casos de ejercicios.
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]
Ejemplo 2. Transformada de Laplace para suma de términos f(t) con desplazamiento, o función «gate» o compuerta
Referencia: Lathi práctica 4.1.a p337
x(t) = \mu (t) - \mu (t-2)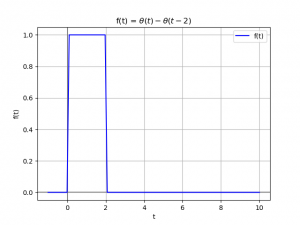
El bloque de ingreso se expresa como:
u = sym.Heaviside(t) ft = u - u.subs(t,t-2)
Al aplicar el algoritmo anterior, modificando la expresión ft, la Transformada de Laplace muestra que el término desplazamiento tiene un componente exponencial.
f(t):
Heaviside(t) - Heaviside(t - 2)
F(s):
-2*s
1 e
- - -----
s s
>>>
Para considerar el término exponencial en el cálculo de polos, se separa el ejercicio en partes con o sin sym.exp(-a*s) cuando se realice el análisis de estabilidad del sistema.
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]
Ejemplo 3 Transformada de Laplace con cos(t)
Referencia: Oppenheim Ejemplo 9.4 p658
Encontrar la transformada de Laplace para:
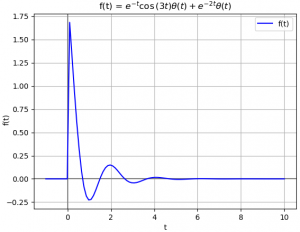
x(t) = e^{-2t}\mu (t) + e^{-t} \cos (3t) \mu (t)
Para el algoritmo, la expresión se escribe como
ft = sym.exp(-2*t)*u + sym.exp(-t)*sym.cos(3*t)*u
con lo que se obtiene como resultado,
f(t):
-t -2*t
e *cos(3*t)*Heaviside(t) + e *Heaviside(t)
F(s):
2
2*s + 5*s + 12
---------------------
3 2
s + 4*s + 14*s + 20
>>>
Para disponer de expresiones mas simples de F(s) en fracciones parciales, se añade la instrucción
Fs = sym.apart(Fs) # separa en fracciones parciales
con lo que se obtiene el siguiente resultado para F(s),
F(s):
s + 1 1
------------- + -----
2 s + 2
s + 2*s + 10
>>>
El primer componente de la suma corresponde a la parte de sym.exp(-t)*sym.cos(3*t) y la segunda parte corresponde a sym.exp(-2*t)
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]
…
Ejemplo 4 Transformada de Laplace con Impulso unitario δ(t) y suma de exponenciales
Referencia: Oppenheim ejemplo 9.5 p661
x(t) = \delta(t) -\frac{4}{3} e^{-t} \mu (t) + \frac{1}{3} e^{2t} \mu (t)La expresión de f(t) podría escribirse directamente como:
d = sym.DiracDelta(t) u = sym.Heaviside(t) ft = d - (4/3)*sym.exp(-t)*u + (1/3)*sym.exp(2*t)*u
Al usar la instrucción sym.laplace_transform(ft,t,s) convierte las fracciones a números reales o con decimales.
Nota: Sympy hasta la versión 1.11.1, las operaciones en el dominio ‘s’ para la Transformadas Inversas de Laplace se encuentran implementadas para manejar principalmente números enteros y fracciones. Los resultados de expresiones combinadas con coeficientes enteros y coeficientes reales no necesariamente se simplifican entre si, pues se manejan diferentes dominios ‘ZZ’ o ‘QQ’. (Revisión 2022-Nov)
Para optimizar la simplificación de expresiones con coeficientes entre enteros y reales, los números reales se convierten a su aproximación racional con la instrucción sym.Rational(0.333333).limit_denominator(100).
Convirtiendo los coeficientes a racionales, se define ft como:
u = sym.Heaviside(t)
d = sym.DiracDelta(t)
# coeficientes como racional en dominio 'ZZ' enteros
k1 = sym.Rational(1/3).limit_denominator(100)
k2 = sym.Rational(4/3).limit_denominator(100)
ft = d - k2*sym.exp(-t)*u + k1*sym.exp(2*t)*u
Al observar los resultados con el algoritmo se puede observar que no se ha procesado el valor de la constante en la transformada.
f(t):
2*t -t
e *Heaviside(t) 4*e *Heaviside(t)
----------------- + DiracDelta(t) - ------------------
3 3
F(s):
1 1
1 - ----- + ----- #faltan las constantes...
s + 1 s - 2
>>>
Se encuentra que la instrucción sym.laplace_transform(ft,t,s) no ha procesado la constante cuando f(t) tiene mas de dos componentes que se multiplican, (Sympy version 1.11.1 revisado hasta 2022-Nov). Asunto que se encuentra a la fecha bajo revisión segun el enlace:
https://github.com/sympy/sympy/issues/23360
Mientras tanto, para obtener resultados e identificado el asunto, se crea una función separa_constante() para un término, donde se separa la constante como el término multiplicador de las partes (args) que no contienen la variable ‘t’.
def separa_constante(termino): ''' separa constante antes de usar sym.laplace_transform(term_suma,t,s) para incorporarla luego de la transformada inconveniente revisado en version 1.11.1 ''' constante = 1 if termino.is_Mul: factor_mul = sym.Mul.make_args(termino) for factor_k in factor_mul: if not(factor_k.has(t)): constante = constante*factor_k termino = termino/constante return([termino,constante])
usando el resultado previo del algoritmo, se prueba la función con el último termino de la suma. Luego de separar la constante, se aplica la transformada de Laplace de Sympy y se incorpora la constante al resultado.
>>> k1 = sym.Rational(1/3).limit_denominator(100) >>> ft = k1*sym.exp(2*t)*u >>> sym.laplace_transform(ft,t,s) (1/(s - 2), 2, True) >>> [termino,constante] = separa_constante(ft) >>> termino exp(2*t)*Heaviside(t) >>> constante 1/3 >>> sym.laplace_transform(termino,t,s)[0]*constante 1/(3*(s - 2))
En el ejemplo se muestra que es necesario separar la constante en al menos dos términos de suma, por lo que se debe considerar el caso de que f(t) sea de uno o varios términos suma. Para simplificar el proceso en los próximos ejercicios se crea la función laplace_term_suma(ft) que se encargará de realizar el proceso término a término.
ft = sym.expand(ft) # expresion de sumas ft = sym.powsimp(ft) # simplifica exponentes term_suma = sym.Add.make_args(ft) Fs = 0 for term_k in term_suma: [term_k,constante] = separa_constante(term_k) Fsk = sym.laplace_transform(term_k,t,s) Fs = Fs + Fsk[0]*constante
Al incorporar las funciones al algoritmo, se puede verificar que se obtienen los resultados obtenidos en la forma analítica.
f(t):
2*t -t
e *Heaviside(t) 4*e *Heaviside(t)
----------------- + DiracDelta(t) - ------------------
3 3
F(s):
4 1
1 - --------- + ---------
3*(s + 1) 3*(s - 2)
>>>
Se prueban todos los ejercicios revisados con sus respuestas y se tiene como algoritmo:
# Transformadas de Laplace Unilateral con Sympy # supone f(t) causal, usa escalón u(t) import sympy as sym # INGRESO t = sym.Symbol('t', real=True) s = sym.Symbol('s') u = sym.Heaviside(t) d = sym.DiracDelta(t) # coeficientes como racional en dominio 'ZZ' enteros k1 = sym.Rational(1/3).limit_denominator(100) k2 = sym.Rational(4/3).limit_denominator(100) ft = d - k2*sym.exp(-t)*u + k1*sym.exp(2*t)*u #ft = d - 3*d.subs(t,t-2) + 2*d.subs(t,t-3) #ft = k2*sym.exp(-2*t)*u - k1*sym.exp(-2*t)*u.subs(t,t-5) #ft = k2*sym.exp(-2*t)*u.subs(t,t-5) #ft = d.subs(t,t-2) #ft = d #ft = 3*sym.exp(-2*t)*u + sym.exp(-t)*sym.cos(3*t)*u #ft = u #ft = u - u.subs(t,t-2) #ft = u.subs(t,t-2) # PROCEDIMIENTO def laplace_transform_suma(ft): '''transformada de Laplace de suma de terminos separa constantes para conservar en resultado ''' def separa_constante(termino): ''' separa constante antes de usar sym.laplace_transform(term_suma,t,s) para incorporarla luego de la transformada inconveniente revisado en version 1.11.1 ''' constante = 1 if termino.is_Mul: factor_mul = sym.Mul.make_args(termino) for factor_k in factor_mul: if not(factor_k.has(t)): constante = constante*factor_k termino = termino/constante return([termino,constante]) # transformadas de Laplace por términos suma ft = sym.expand(ft) # expresion de sumas ft = sym.powsimp(ft) # simplifica exponentes term_suma = sym.Add.make_args(ft) Fs = 0 for term_k in term_suma: [term_k,constante] = separa_constante(term_k) Fsk = sym.laplace_transform(term_k,t,s) Fs = Fs + Fsk[0]*constante # separa exponenciales constantes Fs = sym.expand_power_exp(Fs) return(Fs) Fs = laplace_transform_suma(ft) # SALIDA print('\n f(t): ') sym.pprint(ft) print('\n F(s): ') sym.pprint(Fs)
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]
..
Ejemplo 5 f(t) con Impulsos unitarios desplazados
Referencia: Lathi Ej 4.9c p355
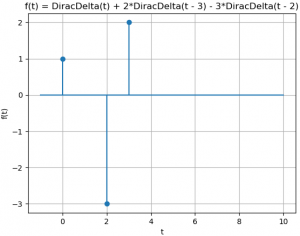
Considera la entrada x(t) como una suma de impulsos desplazados en tiempo y de diferente magnitud.
x(t) = \delta (t) - 3 \delta (t-2) + 2 \delta (t-3)
para el algoritmo del ejercicio 4, se modifica la línea de ingreso a:
ft = d - 3*d.subs(t,t-2) + 2*d.subs(t,t-3)
obteniendo como resultado del algoritmo anterior:
f(t):
DiracDelta(t) + 2*DiracDelta(t - 3) - 3*DiracDelta(t - 2)
F(s):
-2*s -3*s
1 - 3*e + 2*e
>>>
Transformada de Laplace para: [ ej1 un exponencial ] [ ej2 escalón unitario ] [ ej3 con cos(t) ] [ ej4 impulso unitario y sumas] [ ej5 impulso unitario desplazado ]