[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]
..
1. Concepto de alias
Referencia: Downey 2.1 p21
Una definición simplificada de "alias" es de dos nombres para una persona: "Pancho" y "Francisco". De forma semejante, Dos señales diferentes en su forma discreta pueden tener la misma secuencia de valores.
[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]
..
2. Ejemplo
Referencia: McClellan 4.1.2 p127
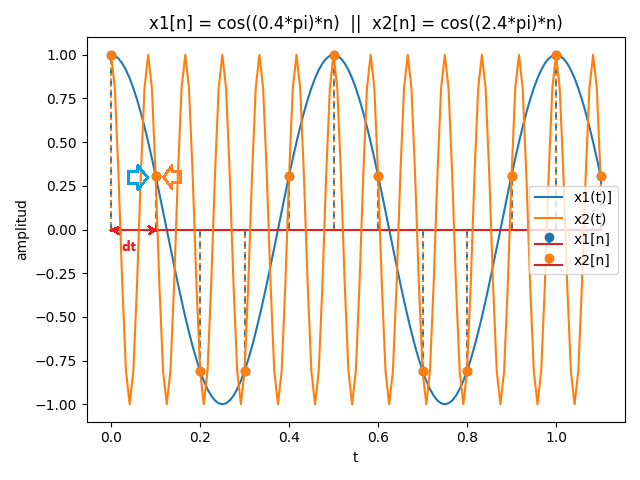
Considere las siguientes señales y compare sus gráficas.
x_1[n] = \cos(0.4\pi n) x_2[n] = \cos(2.4\pi n) = cos(0.4\pi n + 2\pi n ) = cos(0.4\pi n)dado que 2πn es un número entero de periodos de la señal coseno.
Con Python se realiza las gráficas obteniendo las muestras usando fs para observar los puntos sobre x1(t) de ω=0.4π. Para suavizar la curva x(t) se usa fs_veces como sobre-muestreo de la señal y crear la linea azul.
Se compara con x2(t) realizando el mismo proceso, que al unificar las gráficas se observa que los puntos de muestra son válidos para ambas señales x1(t), x2(t).
muestreo: 12 tamaño ki: 12 tamaño ti: 133 fs: 10 ; dt: 0.1 ; fs_veces: 12 cos((0.4*pi)*n) cos((2.4*pi)*n)
La gráfica permite mostrar que las muestras son iguales cuando se repite n veces el valor de tiempo de muestreo dt=1/fs para ambas señales.
Si la frecuencia de x2[n] fuese solamente π, la gráfica muestra la diferencia de valores para x1[n] y x2[n]
x_1[n] = \cos(0.4\pi n) x_2[n] = \cos(\pi n) = cos(0.4\pi n + 0.6\pi n ) = cos(\pi n)muestreo: 12 tamaño ki: 12 tamaño ti: 133 fs: 10 ; dt: 0.1 ; fs_veces: 12 cos((0.4*pi)*n) cos((1.0*pi)*n)
En la gráfica se destaca la diferencia de valores para cada señal luego del primer dt.

[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]
..
3. Algoritmo en Python
# ejercicio 4.2 p128 Muestreo de señales sinusoidales # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym # variables continuas t = sym.Symbol('t', real=True) # variables discretas n = sym.Symbol('n', integer=True, positive=True) pi = sym.pi DosPi = sym.UnevaluatedExpr(2*sym.pi) equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] # INGRESO # usar sym.UnevaluatedExpr() para no simplificar # automaticamente freq angular w>(2*pi) en Sympy with sym.evaluate(False): # no simplificar freq angular w >2*pi w1 = 0.4 w2 = 0.4+2 x1 = sym.cos(w1*pi*n) x2 = sym.cos(w2*pi*n) xn = [x1,x2] xn_etiqueta = ['x1[n]','x2[n]'] xt_etiqueta = ['x1(t)]','x2(t)'] titulo = 'x1[n] = '+str(x1)+' || x2[n] = '+str(x2) nT = 2.25 # periodos a graficar fs = 10 # muestreo discreto fs_veces = 12 # suavizar x(t), sobremuestreo # PROCEDIMIENTO muestras_n = int(nT*(2/w1))+1 x_conteo = len(xn) # muestreo x[n] dt = 1/fs # tamaño de paso con fs ki = np.arange(0,muestras_n,1,dtype=int) # muestreo x(t) dtc = dt/fs_veces # suavizar x(t), sobremuestreo ti = np.arange(0,(muestras_n-1)*dt+dtc, dtc) xn_muestras = {} for i in range(0,x_conteo,1): unasenal = xn[i] xtk = unasenal.subs(n,t*fs) xt = sym.lambdify(t,xtk, modules=equivalentes) xki = xt(ki*dt) xti = xt(ti) xn_muestras[i] = {'ki':ki,'xki':xki, 'ti':ti,'xti':xti,} # SALIDA print('muestreo:',muestras_n) print(' tamaño ki:',len(ki)) print(' tamaño ti:',len(ti)) print('fs:',fs,' ; dt:',dt, ' ; fs_veces:',fs_veces) for unasenal in xn: print(unasenal) # GRAFICA def _graf_lineacolor_i(i): ''' función auxiliar, asigna el color en la paleta de matplotlib acorde al número i entre 0 y 9 ''' if (i<=9): # color de la línea lineacolor = 'C'+str(i) else: numcolor = i%10 lineacolor = 'C'+str(numcolor) return(lineacolor) for i in range(0,len(xn_muestras),1): color_i = _graf_lineacolor_i(i) estilo_i = ':' # estilo de la línea if i%2 == 0: #es impar estilo_i = '--' # muestreo x[n] ki = xn_muestras[i]['ki'] xki = xn_muestras[i]['xki'] puntofmt = color_i + estilo_i plt.stem(ki*dt, xki, linefmt = puntofmt, label=xn_etiqueta[i]) # muestreo x(t) ti = xn_muestras[i]['ti'] xti = xn_muestras[i]['xti'] plt.plot(ti,xti, '-', color = color_i, label=xt_etiqueta[i]) #plt.axhline(0,color='black') plt.xlabel('t') plt.ylabel('amplitud') plt.title(titulo) plt.tight_layout() plt.legend() plt.show()
[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]
..
4. Ejercicios con alias
Referencia: McClellan ejercicio 42 p128
Muestre que x2[n] es un alias de x1[n] y encuentre dos frecuencias que sean alias de 0.4π rad.
x1[n] = 7 cos(0.4π n - 0.2π)
x2[n] = 7 cos(8.4π n - 0.2π) = cos(0.4π n + 4(2π n) - 0.2π ) = cos(0.4π n- 0.2π)
Usando el algoritmo del numeral anterior se realiza la gráfica.
muestreo: 7 tamaño ki: 7 tamaño ti: 272 fs: 10 ; dt: 0.1 ; fs_veces: 45 cos((0.4*pi)*n - 0.2*pi) cos((8.4*pi)*n - 0.2*pi)

Usando los parámetros de entrada:
# INGRESO # usar sym.UnevaluatedExpr() para no simplificar # automaticamente freq angular w>(2*pi) en Sympy with sym.evaluate(False): # no simplificar freq angular w >2*pi w1 = 0.4 w2 = 0.4+8 x1 = sym.cos(w1*pi*n-0.2*pi) x2 = sym.cos(w2*pi*n-0.2*pi) xn = [x1,x2] xn_etiqueta = ['x1[n]','x2[n]'] xt_etiqueta = ['x1(t)]','x2(t)'] titulo = 'x1[n] = '+str(x1)+' || x2[n] = '+str(x2) nT = 1.25 # periodos a graficar fs = 10 # muestreo discreto fs_veces = 45 # suavizar x(t), sobremuestreo
Para los alias se usa la frecuencia normalizada en radianes: ωrad , considerando que si se suma varias veces 2π se obtiene un alias.
ωalias= 0.4π + 2π k ; donde k = 0,1,2,3...
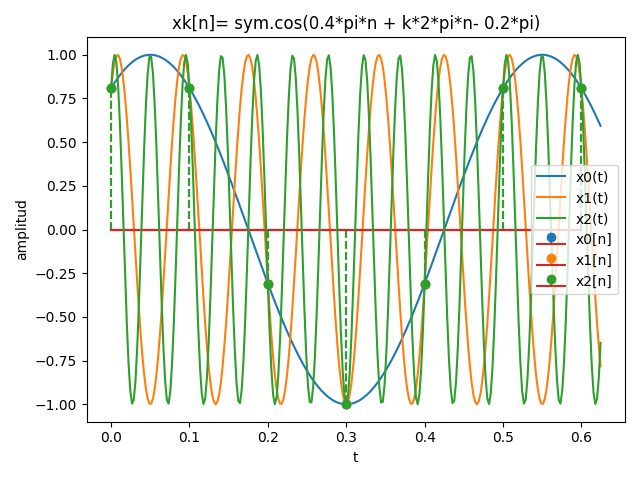
5. Alias Principal
El alias principal se define como la frecuencia ω única en el intervalo entre
-π <ωalias < π , que para el ejercicio es 0.4π por lo que se propone usar como alias:
x0[n] = 7 cos((0.4π + 0(2π) )n - 0.2π)
x1[n] = 7 cos((0.4π + 1(2π) )n - 0.2π)
x2[n] = 7 cos((0.4π + 2(2π) )n - 0.2π)
muestreo: 7 tamaño ki: 7 tamaño ti: 272 fs: 10 ; dt: 0.1 ; fs_veces: 45 cos((0.4*pi)*n - 0.2*pi) cos((2.4*pi)*n - 0.2*pi) cos((4.4*pi)*n - 0.2*pi)
El bloque de ingreso para el algoritmo y el número de muestras para el periodo de la señal de menor frecuencia angular es referenciado a ω0.
# INGRESO # usar sym.UnevaluatedExpr() para no simplificar # automaticamente freq angular w>(2*pi) en Sympy with sym.evaluate(False): # no simplificar freq angular w >2*pi w0 = 0.4 w1 = 0.4+2 w2 = 0.4+4 x0 = sym.cos(w0*pi*n - 0.2*pi) x1 = sym.cos(w1*pi*n - 0.2*pi) x2 = sym.cos(w2*pi*n - 0.2*pi) xn = [x0,x1,x2] xn_etiqueta = ['x0[n]','x1[n]','x2[n]'] xt_etiqueta = ['x0(t)','x1(t)','x2(t)'] titulo = 'xk[n]= sym.cos(0.4*pi*n + k*2*pi*n- 0.2*pi)' nT = 1.25 # periodos a graficar fs = 10 # muestreo discreto fs_veces = 45 # suavizar x(t), sobremuestreo # PROCEDIMIENTO muestras_n = int(nT*(2/w0))+1
[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]
..
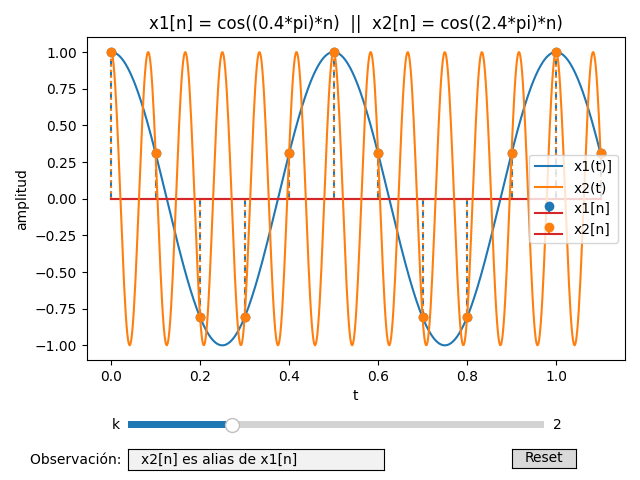
5. Gráfico interactivo
Se añade en la fórmula de la señal x2[n] el valor de k como control para el gráfico:
El gráfico interactivo resultante se actualiza x2[n] y el título, también se muestra en los resultados si hay el "alias".
muestras: 12 tamaño ki: 12 tamaño ti: 606 fs: 10 ; dt: 0.1 ; fs_veces: 55 cos((0.4*pi)*n) cos((2.4*pi)*n) k: 1 x2[n] NO es alias de x1[n] k: 2 x2[n] es alias de x1[n] k: 3 x2[n] NO es alias de x1[n] k: 4 x2[n] es alias de x1[n] k: 5 x2[n] NO es alias de x1[n] k: 6 x2[n] es alias de x1[n] k: 7 x2[n] NO es alias de x1[n]
5.1 Algoritmo interactivo en Python
Se actualiza la parte gráfica a la forma de objetos fig, graf para crear los objetos interactivos de barra de desplazamiento (slider) k , botón Reset y cuadro de texto para la observación si es o no alias.
# ejercicio 4.2 p128 Muestreo de señales sinusoidales # grafico interactivo con k # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym # variables continuas t = sym.Symbol('t', real=True) # variables discretas n = sym.Symbol('n', integer=True, positive=True) pi = sym.pi DosPi = sym.UnevaluatedExpr(2*sym.pi) equivalentes = [{'DiracDelta': lambda x: 1*(x==0)}, {'Heaviside': lambda x,y: np.heaviside(x, 1)}, 'numpy',] # INGRESO # usar sym.UnevaluatedExpr() para no simplificar # automaticamente freq angular w>(2*pi) en Sympy with sym.evaluate(False): # no simplificar freq angular w >2*pi w1 = 0.4 k = 2 w2 = 0.4+k x1 = sym.cos(w1*pi*n) x2 = sym.cos(w2*pi*n) xn = [x1,x2] xn_etiqueta = ['x1[n]','x2[n]'] xt_etiqueta = ['x1(t)]','x2(t)'] titulo = 'x1[n] = '+str(x1)+' || x2[n] = '+str(x2) nT = 2.25 # periodos a graficar fs = 10 # muestreo discreto fs_veces = 55 # suavizar x(t), sobremuestreo # PROCEDIMIENTO muestras_n = int(nT*(2/w1))+1 x_conteo = len(xn) # muestreo x[n] dt = 1/fs # tamaño de paso con fs ki = np.arange(0,muestras_n,1,dtype=int) # muestreo x(t) dtc = dt/fs_veces # para x(t) ti = np.arange(0,(muestras_n-1)*dt+dtc, dtc) xn_muestras = {} for i in range(0,x_conteo,1): unasenal = xn[i] xtk = unasenal.subs(n,t*fs) xt = sym.lambdify(t,xtk, modules=equivalentes) xki = xt(ki*dt) xti = xt(ti) xn_muestras[i] = {'ki':ki,'xki':xki, 'ti':ti,'xti':xti,} if k%2==0: observa = 'x2[n] es alias de x1[n]' else: observa = 'x2[n] NO es alias de x1[n]' # SALIDA print('muestras:',muestras_n) print(' tamaño ki:',len(ki)) print(' tamaño ti:',len(ti)) print('fs:',fs,' ; dt:',dt, ' ; fs_veces:',fs_veces) for unasenal in xn: print(unasenal) # GRAFICA interactiva from matplotlib.widgets import Slider, Button, TextBox def _graf_lineacolor_i(i): ''' función auxiliar, asigna el color en la paleta de matplotlib acorde al número i entre 0 y 9 ''' if (i<=9): # color de la línea lineacolor = 'C'+str(i) else: numcolor = i%10 lineacolor = 'C'+str(numcolor) return(lineacolor) fig, grf = plt.subplots() puntos = [] ; lineas = [] for i in range(0,len(xn_muestras),1): color_i = _graf_lineacolor_i(i) estilo_i = ':' # estilo de la línea if i%2 == 0: #es impar estilo_i = '--' # muestreo x[n] ki = xn_muestras[i]['ki'] xki = xn_muestras[i]['xki'] puntofmt = color_i + estilo_i puntoi = grf.stem(ki*dt, xki, linefmt = puntofmt, label=xn_etiqueta[i]) # muestreo x(t) ti = xn_muestras[i]['ti'] xti = xn_muestras[i]['xti'] lineai, = grf.plot(ti,xti, '-', color = color_i, label=xt_etiqueta[i]) puntos.append(puntoi) lineas.append(lineai) #plt.axhline(0,color='black') grf.set_xlabel('t') grf.set_ylabel('amplitud') grf.set_title(titulo) plt.tight_layout() plt.legend() #plt.show() # grafica elementos interactivos plt.subplots_adjust(bottom=0.25) # espacio widgets # slider: barras para valores # amplitud slider [x,y,ancho,alto] k_donde = plt.axes([0.2, 0.10, 0.65, 0.03]) k_slider = Slider(k_donde, 'k', 0, 8, valinit=k,valstep= 1, orientation='horizontal') txt_donde = plt.axes([0.2, 0.02, 0.4, 0.045]) txt_observa = TextBox(txt_donde, "Observación: ", initial=observa) #text_box.on_submit(submit) def stem_update(puntos,xdata,ydata,grafico): '''actualiza puntos/tallos de plt.stem con los datos de cada eje en un gráfico ''' puntos.markerline.set_xdata(xdata) puntos.markerline.set_ydata(ydata) segmentos=[] # tallos o troncos for j in range(0,len(xdata),1): segmentos.append([[xdata[j],0], [xdata[j],ydata[j]]]) puntos.stemlines.set_segments(segmentos) puntos.baseline.set_xdata([xdata[0],xdata[-1]]) grafico.relim() grafico.autoscale_view() return(puntos,grafico) def grafico_actualiza(val): # actualiza valores x,y k = k_slider.val with sym.evaluate(False): w2 = 0.4+k x2 = sym.cos(w2*pi*n) xn[1] = x2 titulo = 'x1[n] = '+str(x1)+' || x2[n] = '+str(x2) i = 1 unasenal = xn[i] xtk = unasenal.subs(n,t*fs) xt = sym.lambdify(t,xtk, modules=equivalentes) xki = xt(ki*dt) xti = xt(ti) xn_muestras[i] = {'ki':ki,'xki':xki, 'ti':ti,'xti':xti,} # actualiza grafico stem_update(puntos[1],ki*dt,xki,grf) lineas[i].set_ydata(xti) grf.set_title(titulo) fig.canvas.draw_idle() # actualiza figura # observación if k%2==0: observa = 'x2[n] es alias de x1[n]' else: observa = 'x2[n] NO es alias de x1[n]' txt_observa.set_val(observa) print('k:',k,observa) # boton reinicio de gráfica btn_rstdonde = plt.axes([0.8, 0.025, 0.1, 0.04]) btn_rst = Button(btn_rstdonde, 'Reset', hovercolor='0.975') def grafico_reinicia(event): k_slider.reset() return() # objetos interactivos k_slider.on_changed(grafico_actualiza) btn_rst.on_clicked(grafico_reinicia) plt.show()
[ alias ] [ ejemplo ] [ algoritmo ] [ ejercicio ] [ gráfico interactivo ]