DFT: [ impulso unitario ] [ pulso rectangular ] [ exponencial complejo ] [ algoritmo ]
La DFT es una versión discreta del espectro de frecuencias de tipo X(ejω ) que es contínua y conocida como DTFT. Se puede construir pares de DFT haciendo la sustitución ω=(2π/N)/k en un par DTFT
1. DFT de un impulso unitario desplazado
Referencia: McClellan 8.1.2.1 p306. Transformada de Fourier – Señales aperiódicas continuas
Tomando la DFT de x[n] =δ[n], la sumatoria de DFT se simplifica a un término
X[k] = \sum_{n=0}^{N-1} \delta [n] e^{-j(2\pi k/N)n} = \delta [0] e^{-j(2\pi k/N)(0)} + \sum_{n=1}^{N-1} \cancel{\delta [n]} e^{-j(2\pi k/N)n} = \delta [0] (1) + 0 = 1Usando la respuesta anterior, para x[n] = δ[n-nd]m se puede escribir
X[k] = \delta [n_d] e^{-j(2\pi k/N)n_d} = e^{-j\omega n_d} \delta [n-n_d] \leftrightarrow e^{-j\omega n_d}
Se crea a partir de una función rectangular con ancho igual al tamaño de paso.
# INGRESO L = 50 # Tramos en un periodo # señal es impulso unitario periódico d[n], rectangular ancho "pequeño" f0 = 0.2 # frecuencia fundamental de señal ancho = 1/f0/L # ancho del impulso rectangular n0 = 0.5 # desplazamiento en tiempo xt = lambda n: np.heaviside(n-n0,1)-np.heaviside(n-n0-ancho,1) # para DFT N = 1*L # N par mayor que L, tramos DFT, FFT
DFT: [ impulso unitario ] [ pulso rectangular ] [ exponencial complejo ] [ algoritmo ]
..
2. DFT de un pulso rectangular
Referencia: Transformada de Fourier – Señales aperiódicas continuas
Para un pulso rectangular en el domino de tiempo discreto, expresado como:
r [n] = \begin {cases} 1 & 0\leq n \leq L-1 \\ 0 & L \leq n \leq N-1 \end {cases}La DFT tiene un término de la forma
R_L[k] = R_L \Big( e^{j\omega} \Big) = \frac{\sin \Big( \frac{1}{2} L(2\pi k/N)\Big)}{\sin \Big( \frac{1}{2} (2\pi k/N)\Big)} e^{-j(2 \pi k/N)(L-1)/2}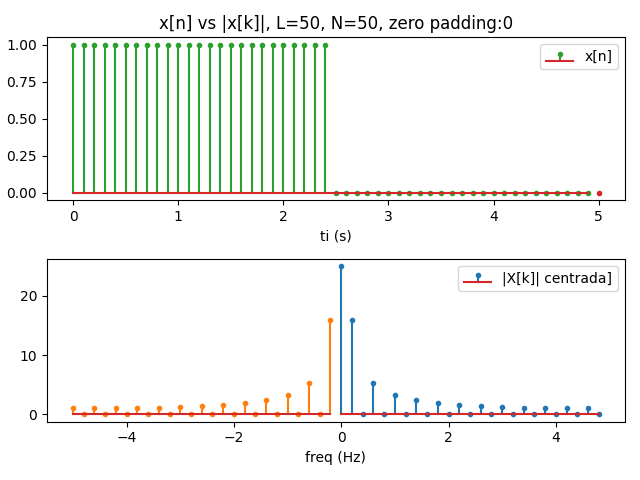
Se crea a partir de una función rectangular con ancho igual a la mitad de un periodo.
# INGRESO L = 50 # Tramos en un periodo # señal es rectangular periódico rect[n] f0 = 0.2 # frecuencia fundamental de señal ancho = 0.5*(1/f0) # ancho del impulso rectangular xt = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1) # para DFT N = 1*L # N par mayor que L, tramos DFT
DFT: [ impulso unitario ] [ pulso rectangular ] [ exponencial complejo ] [ algoritmo ]
..
3. DFT de un exponencial complejo
Una señal exponencial compleja de tamaño finito se expresa como
x [n] = r_L[n] e^{j \omega_0 n}= \begin {cases} e^{j\omega_0 n} & 0\leq n \leq L-1 \\ 0 & L \leq n \leq N-1 \end {cases}La DFT tiene un término de la forma
X[k] = R_L \Big( e^{j\omega-\omega_0} \Big) = \frac{\sin \Big( \frac{1}{2} L(2\pi k/N - \omega_0)\Big)}{\sin \Big( \frac{1}{2} (2\pi k/N- \omega_0)\Big)} e^{-j(2 \pi k/N- \omega_0)(L-1)/2}expresión que también se representa en términos de Dirichlet
X[k] = D_L(2\pi k/N - \omega_0) e^{-j(2 \pi k/N- \omega_0)(L-1)/2}Dado que el exponencial solo contribuye a la fase, el resultado muestra que la magnitud depende solo del termino DL
La DFT es muy simple cuando la frecuencia de la señal exponencial es un múltiplo entero de 2π/N y la cantidad de muestras DFT son iguales a la cantidad de muestras de la señal N=L.
X[k] = N \delta [k-k_0]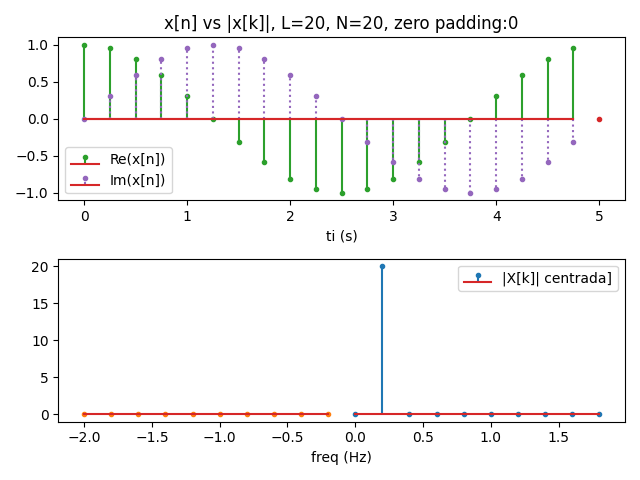
Para N=2L, la gráfica adquiere mayor resolución en el dominio de la frecuencia, donde se requiere completar los puntos L para que sean iguales a N y realizar el cálculo de fft.
Se crea a partir de una función exponencial multiplicada por una rectangular con ancho igual a un periodo. Para la gráfica se considera solo la parte real de la función.
# INGRESO L = 20 # Tramos en un periodo # señal es exponencial complejo periódico f0 = 0.2 # frecuencia fundamental de señal ancho = 1*(1/f0) # ancho del impulso rectangular rect = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1) xt = lambda t: rect(t)*np.exp(1j*2*np.pi*f0*t) # para DFT N = 2*L # N par mayor que L, tramos DFT
DFT: [ impulso unitario ] [ pulso rectangular ] [ exponencial complejo ] [ algoritmo ]
..
4. Algoritmo en Python
Se adjunta el algoritmo para los ejercicios, el bloque de ingreso presentado corresponde al ejercicio de exponencial complejo. Para los otros ejercicios actualizar el bloque de INGRESO
# ejemplo 8.1.2.2 p307 DFT x[n] zero-padding # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt # INGRESO L = 20 # Tramos en un periodo # señal es exponencial complejo periódico f0 = 0.2 # frecuencia fundamental de señal ancho = 1*(1/f0) # ancho del impulso rectangular rect = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1) xt = lambda t: rect(t)*np.exp(1j*2*np.pi*f0*t) # para DFT N = 2*L # N par mayor que L, tramos DFT # PROCEDIMIENTO # muestreo de señal x[n] t0 = 0 ; tn = 1/f0 # intervalo [t0,tn] dt = (tn-t0)/L ti = np.arange(t0,tn,dt) xn = xt(ti) # verificar que L<=N if L<=N: # DFT transformada rapida de Fourier Xk = np.fft.fft(xn,n=N) Xkmagn = np.abs(Xk) # para gráfica Xkfase = np.angle(Xk) freq_Hz = np.fft.fftfreq(N,dt) # frecuencias en Hz mitad = int(N/2) k0 = np.argmax(Xk) # Pico |X[k]| # SALIDA if N>=L: print('k0:',k0,'; i:',mitad+k0) print('freq_Hz:',freq_Hz[k0], '; Xk[k0]:',Xk[k0]) print('[ i, freq[ki],|X[k]| ,X[k]]') kmin = k0-4 ; kmax = k0+4 if kmin<0: kmin = 0 if kmax>N: kmax = N for i in range(kmin,kmax,1): print([i,freq_Hz[i],Xkmagn[i],Xk[i]]) else: print('Revisar: L debe ser menor o igual a N') print('L:',L,'; N:',N) # GRAFICA if N>=L: LN_texto= ', L='+str(L)+', N='+str(N) zp_texto = 'zero padding:'+str(N-L) plt.subplot(211) plt.stem(ti,np.real(xn),label='Re(x[n])', markerfmt ='C2.',linefmt='C2-') plt.stem(ti,np.imag(xn),label='Im(x[n])', markerfmt ='C4.',linefmt='C4:') plt.stem(L*dt,0,markerfmt ='C3.') plt.xlabel('ti (s)') plt.title('x[n] vs |x[k]|'+LN_texto+', '+zp_texto) plt.legend() plt.subplot(212) plt.stem(freq_Hz[0:mitad], Xkmagn[0:mitad], label='|X[k]| centrada]', markerfmt ='C0.',linefmt='C0-') plt.stem(freq_Hz[mitad:], Xkmagn[mitad:], markerfmt ='C1.',linefmt='C1-') plt.xlabel('freq (Hz)') plt.legend() plt.tight_layout() plt.show()
DFT: [ impulso unitario ] [ pulso rectangular ] [ exponencial complejo ] [ algoritmo ]