[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
1. Suma por Fasores
Referencia: McClellan 2.6 p48
Con señales de igual frecuencia en el mismo medio de transmisión las señales se suman. Una forma simplificada de sumar señales con diferente amplitud, fase e igual frecuencia es por medio de fasores , considerando:
x(t) = \sum_{k=1}^{N} A_k \cos(\omega_0 t + \varphi_k) = A \cos(\omega_0 t + \varphi)Se puede representar los cosenos en forma compleja
A \cos(\omega_0 t + \varphi) = \Re \Big\{ A e^{j(\omega_0 t + \varphi)} \Big\} = \Re \Big \{ A e^{j\varphi} e^{j \omega_0 t} \Big\} \sum_{k=1}^{N} A_k e^{j\varphi_k} = A e^{j \varphi}[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
2. Ejemplo – regla de suma de fasores
Referencia: McClellan 2.6.3 p51
Sumar dos señales sinusoidales de igual frecuencia usando fasores:
x_1 (t) = 1.7\cos(20 \pi t + 70\pi / 180) x_2 (t) = 1.9\cos(20 \pi t + 200\pi / 180)[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
3. Desarrollo analítico
La frecuencia es 10 Hz para ambas señales.
Las suma de x1(t) + x2(t) mediante fasores tiene cuatro pasos:
1. cada señal se escribe usando fasores:
X_1 = 1.7e^{j 70\pi / 180} X_2 = 1.9e^{j 200\pi / 180}2. cada fasor se escribe en forma compleja (rectangular):
X_1 = 0.5814 + j 1.5975 X_2 = -1.7854 - j 0.64983. se suman las partes reales e imaginarias
X_3 = X_1 + X_2 = (0.5814 + j 1.5975) + (-1.7854 - j 0.6498) = -1.204 + j 0.94774.Se reescribe a la forma polar y luego a senoidal con la frecuencia de las señales
X_3 = 1.5322 e^{j 141.79\pi/180} x_3(t) = 1.5322\cos(20\pi t +141.79\pi /180)[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
4. Algoritmo con Sympy
Las señales en el bloque de ingreso son:
x1 = 1.7*sym.cos(20*pi*t+70*pi/180) x2 = 1.9*sym.cos(20*pi*t+200*pi/180)
Desarrollando solo para x1(t) se obtienen los parámetros de un término coseno,
x1_args = dsp.cos_args_one_term(x1) amplitud = x1_args['amplitud'] fase = x1_args['fase']
El fasor se obtiene escribiendo las expresiones con amplitud y fase,
fasor1 = amplitud*sym.exp(I*fase)
para la forma de números complejos, se usa sym.expand(fasor1,complex=True),
>>> fasor1 1.7*exp(7*I*pi/18) >>> sym.expand(fasor1,complex=True) 1.7*cos(7*pi/18) + 1.7*I*sin(7*pi/18) >>> sym.expand(fasor1,complex=True).evalf() 0.581434243653637 + 1.59747745533604*I >>>
sin embargo la expresión muestra el cos() para la parte real y sin() para la imaginaria. La expresión las evalúa la funciones senoidales añadiendo .evalf() al final de la instrucción, quedando la instrucción de la siguiente forma:
fasor1_complex = sym.expand(fasor1,complex=True).evalf()
El proceso se repite para la señal x2(t) para luego sumar los fasores en forma compleja, siempre y cuando las frecuencias sean iguales.
Para mantener la amplitud del fasor_suma con signo positivo, evitando que Sympy simplifique la fase con π se usa la instrucción sym.UnevaluatedExpr(fase).
El resultado del algoritmo se muestra a continuación:
fasor1: 1.7*exp(7*I*pi/18) fasor1_complex: 0.581434243653637 + 1.59747745533604*I fasor2: 1.9*exp(-8*I*pi/9) fasor2_complex: -1.78541597949323 - 0.649838272318771*I fasor_suma_complex: -1.20398173583959 + 0.947639183017274*I fasor_suma: 1.53218538089389*exp(-0.666817831701547 + pi) x_suma: 1.53218538089389*cos(10*t*(2*pi) - (0.666817831701547 + pi)) >>>
Las instrucciones en Python son:
# ejemplo 2.6.3 p52 Suma de Fasores y graf_polar # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables continuas from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x1 = 1.7*sym.cos(20*pi*t+70*pi/180) x2 = 1.9*sym.cos(20*pi*t+200*pi/180) # PROCEDIMIENTO # señal x1 x1_args = dsp.cos_args_one_term(x1) amplitud = x1_args['amplitud'] fase = x1_args['fase'] fasor1 = amplitud*sym.exp(I*fase) # fasor números complejos fasor1_complex = sym.expand(fasor1,complex=True).evalf() # señal x2 x2_args = dsp.cos_args_one_term(x2) amplitud = x2_args['amplitud'] fase = x2_args['fase'] fasor2 = amplitud*sym.exp(I*fase) # fasor números complejos fasor2_complex = sym.expand(fasor2,complex=True).evalf() # suma de fasores de x1(t) y x2(t) en la misma freq if x1_args['freq_Hz'] == x2_args['freq_Hz']: freq_iguales = True fasorsum_complex = fasor1_complex + fasor2_complex amplitud = sym.Abs(fasorsum_complex) fase = sym.arg(fasorsum_complex) fasor_suma = amplitud*sym.exp(sym.UnevaluatedExpr(fase)) x_suma = amplitud*sym.cos(DosPi*x1_args['freq_Hz']*t+sym.UnevaluatedExpr(fase)) x_suma_args = dsp.cos_args_one_term(x_suma) else: # diferentes frecuencias freq_iguales = False fasorsum_complex = 0+0j fasor_suma = fasor1 +fasor2 x_suma = x1+x2 # SALIDA print('fasor1:',fasor1) print('fasor1_complex:',fasor1_complex) print('fasor2:',fasor2) print('fasor2_complex:',fasor2_complex) if freq_iguales: print('fasor_suma_complex:',fasorsum_complex) print('fasor_suma:',fasor_suma) else: print(' las frecuencias no son iguales en x1(t) y x2(t)') print('x_suma:',x_suma)
[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
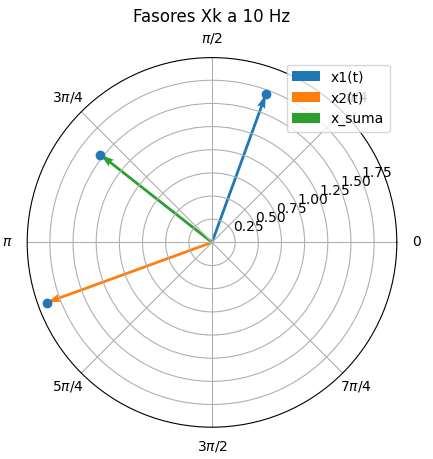
5. Gráfica de fasores
La gráfica de fasores es de tipo polar con flechas que parten desde el centro y se dibujan usando la amplitud y fase por cada fasor.
Primero se genera la lista de x_amplitud y x_fase, la suma se añade solamente si las señales son de igual frecuencia.
La forma polar de la gráfica se indica con projection='polar' al definir el sub-gráfico. Como referencia se añade puntos al final de cada fasor y se diferencian al usar un color diferente.
La instrucción de flechas, requiere el punto de partida (0,0) y el punto de llegada para cada fasor (x_fase[i],x_amplitud[i]).
Las etiquetas del gráfico se muestran en radianes
Instrucciones adicionales para la gráfica polar
# GRAFICA de suma de fasores x_etiqueta = ['x1(t)','x2(t)'] x_amplitud = [float(x1_args['amplitud']), float(x2_args['amplitud'])] x_fase = [float(x1_args['fase']), float(x2_args['fase'])] if freq_iguales: x_amplitud.append(float(x_suma_args['amplitud'])) x_fase.append(float(x_suma_args['fase'])) x_etiqueta.append('x_suma') # graficar fig_polar = plt.figure() graf_polar = fig_polar.add_subplot(projection='polar') punto = graf_polar.plot(x_fase,x_amplitud,'o',xunits='radians') for i in range(0,len(x_amplitud),1): if (i<=9): # color de la línea lineacolor = 'C'+str(i) else: numcolor = i%10 lineacolor = 'C'+str(numcolor) graf_polar.quiver(0,0,x_fase[i],x_amplitud[i], angles='xy', scale_units='xy', scale=1, label = x_etiqueta[i], color = lineacolor) # actualiza etiquetas de gráfico polar etiquetas = ['0', '$\pi$/4', '$\pi$/2','3$\pi$/4', '$\pi$','5$\pi$/4','3$\pi$/2','7$\pi$/4'] dtheta = int(360/len(etiquetas)) lines, labels = plt.thetagrids(range(0, 360,dtheta), etiquetas) graf_polar.set_title('Fasores Xk a '+str(x1_args['freq_Hz'])+ ' Hz') graf_polar.legend() plt.show()
[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]
..
6. Función
6.1 Incorporar parámetro fasor a dsp.cos_args_one_term()
El fasor puede considerarse como parte de los parámetros de una señal, por lo que el cálculo se incorpora a la instrucción dsp.cos_args_one_term() como parámetro: 'fasor' y 'fasor_complex'.
La disponibilidad del parámetro 'fasor' puede facilitar las operaciones de suma de señales de igual frecuencia cuando se usen mas componentes de la señal. La simplificación del algoritmo se muestra en el siguiente ejercicio:
6.2 Ejercicio
Referencia: McClellan ejercicio 2.8 p54
Considere las dos señales:
x_1 (t) = 5\cos(2 \pi (100) t + \pi /3) x_2 (t) = 4\cos(2 \pi(100) t + \pi / 4)6.3 Algoritmo en Python
Considerando que se pueden usar mas señales de igual frecuencia para sumar los fasores, se procede a usar x_senales como una lista de señales a ser analizada, junto a x_etiqueta con las etiquetas para las gráficas.
# INGRESO x1 = 5*sym.cos(DosPi*100*t + pi/3) x2 = 4*sym.cos(DosPi*100*t - pi/4) x_senales = [x1,x2] # sumar fasores de igual frecuencia x_etiqueta = ['x1(t)','x2(t)']
La revisión de las frecuencias de cada señal se realiza con el diccionario x_freq que tendra el 'conteo' de señales con la misma frecuencia y 'fasor_complex' que se acumulará cada vez que se encuentre una señal de igual frecuencia en la lista x_senales.
Luego se realiza una revisión de las frecuencias que tienen conteo>1 para generar la senal x_suma y añadir a la lista x_senales con la etiqueta correspondiente en x_etiqueta. Se debe actualizar el x_conteo que es usado para enumerar las gráficas.
La salida del algoritmo para el ejercicio se presenta como:
freq_Hz: 100 conteo : 2 fasor_complex : 5.32842712474619 + 1.501699894176*I senal : 5.53599477925144*cos(100*t*(2*pi) + 0.27470298976466)
Las simplificación del algoritmo usando la función actualizada y las señales en una lista se muestran a continuación:
Instrucciones en Python.
# ejercicio 2.8 p54 Suma de Fasores y graf_polar # telg1034 DSP fiec-espol edelros@espol.edu.ec import numpy as np import matplotlib.pyplot as plt import sympy as sym import telg1034 as dsp # variables continuas from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes # INGRESO x1 = 5*sym.cos(DosPi*100*t + pi/3) x2 = 4*sym.cos(DosPi*100*t - pi/4) x_senales = [x1,x2] # sumar fasores de igual frecuencia x_etiqueta = ['x1(t)','x2(t)'] # PROCEDIMIENTO x_conteo = len(x_senales) # sumar fasores por frecuencias iguales x_freq = {} for unasenal in x_senales: xk_args = dsp.cos_args_one_term(unasenal) freq_k = xk_args['freq_Hz'] fasor_complex_k = xk_args['fasor_complex'] if freq_k in x_freq: # sumar fasores en la freq_k x_freq[freq_k]['conteo'] = x_freq[freq_k]['conteo'] + 1 fasor_complex = x_freq[freq_k]['fasor_complex'] x_freq[freq_k]['fasor_complex'] = fasor_complex + fasor_complex_k else: # primer fasor en freq_k x_freq[freq_k] = {} x_freq[freq_k]['conteo'] = 1 x_freq[freq_k]['fasor_complex'] = fasor_complex_k # señal x_suma(t) por frecuencias for unafreq in x_freq: if x_freq[unafreq]['conteo']>1: # existe x_suma fasor_complex = x_freq[unafreq]['fasor_complex'] amplitud = sym.Abs(fasor_complex) fase = sym.arg(fasor_complex) fasor_suma = amplitud*sym.exp(sym.UnevaluatedExpr(fase)) x_suma = amplitud*sym.cos(DosPi*unafreq*t+sym.UnevaluatedExpr(fase)) x_freq[unafreq]['senal'] = x_suma # actualiza lista de señales x_senales.append(x_suma) x_etiqueta.append('x_'+str(unafreq)+'Hz') x_conteo = len(x_senales) # SALIDA for unafreq in x_freq: print('freq_Hz:',unafreq) for unparametro in x_freq[unafreq]: print(' ',unparametro,':', x_freq[unafreq][unparametro])
6.4 funciones para gráficas
En el desarrollo de las gráficas una operación recurrente es encontrar el periodo máximo T_max, por lo que periodo_minmax(x_freq) que se incorpora a telg1034.py.
De forma semejante se requiere un color diferente por cada componente de señal en x_senales dado por su índice en la lista con la función auxiliar . De esa forma se facilita la identificación entre la gráfica de fasores y la gráfica de tiempo _graf_lineacolor_i(i).
Para las gráficas de la suma de fasores y señales en tiempo se requiere realizar las listas de parámetros para cada gráfica.
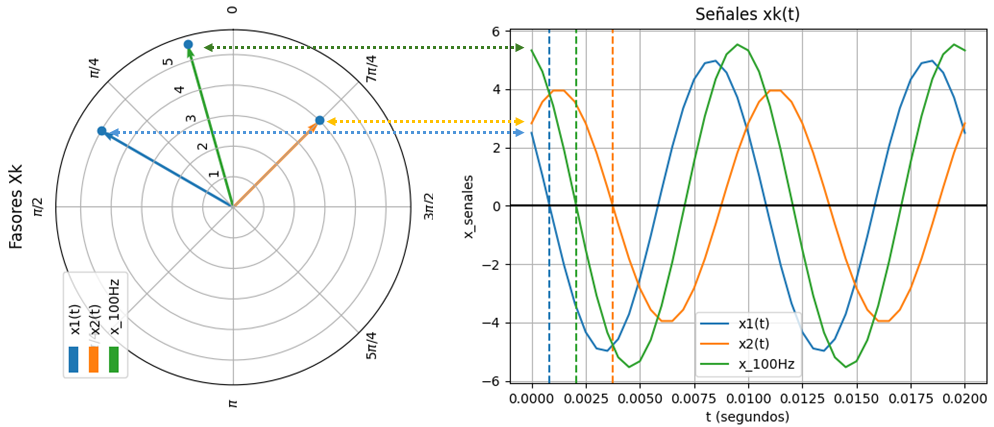
Se destaca la relación entre las gráfica de fasores y en tiempo al rotar graf_polar como se muestra en la imagen.
Instrucciones adicionales para las gráficas
# GRAFICA de suma de fasores --------- # PROCEDIMIENTO de suma de fasores x_amplitud = [] ; x_fase = [] ; x_ceros = [] for unasenal in x_senales: parametro = dsp.cos_args_one_term(unasenal) freq_k = parametro['freq_Hz'] ampl_k = parametro['amplitud'] fase_k = parametro['fase'] x_amplitud.append(float(ampl_k)) x_fase.append(float(fase_k)) # marca un cero cos(wt+p)=0; wt+p=pi/2 # t_cero = (pi/2-p)/w = (pi/2-p)/(2*pi*f) uncero = sym.nan # si es una constante if abs(freq_k)>0: uncero = (pi/2 - fase_k)/(2*pi*freq_k) uncero = np.around(float(uncero),decimals=15) x_ceros.append(uncero) # graficar def _graf_lineacolor_i(i): ''' función auxiliar, asigna el color en la paleta de matplotlib acorde al número i entre 0 y 9 ''' if (i<=9): # color de la línea lineacolor = 'C'+str(i) else: numcolor = i%10 lineacolor = 'C'+str(numcolor) return(lineacolor) fig_polar = plt.figure() graf_polar = fig_polar.add_subplot(projection='polar') punto = graf_polar.plot(x_fase,x_amplitud,'o',xunits='radians') for i in range(0,len(x_amplitud),1): graf_polar.quiver(0,0,x_fase[i],x_amplitud[i], angles='xy', scale_units='xy', scale=1, label = x_etiqueta[i], color = _graf_lineacolor_i(i)) # actualiza etiquetas de gráfico polar etiquetas = ['0', '$\pi$/4', '$\pi$/2','3$\pi$/4', '$\pi$','5$\pi$/4','3$\pi$/2','7$\pi$/4'] dtheta = int(360/len(etiquetas)) lines, labels = plt.thetagrids(range(0, 360,dtheta), etiquetas) graf_polar.set_title('Fasores Xk') graf_polar.legend() #plt.show() # GRAFICAR x(t) --------------------------- # INGRESO tramos_T = 20 # tramos por periodo periodos_graf = 2 # periodos en una grafica # PROCEDIMIENTO GRAFICA # periodo máximo y mínimo de señales def periodo_minmax(x_freq): ''' función auxiliar: obtiene T_max y T_min de una lista de frecuencias x_freq ingresa: x_freq salida: [T_max,Tmin]. Si la frecuencia es cero, T_max=1,T_min=1 ''' T_max = 1 ; T_min = 1 freq = np.array(list(x_freq)) freq_min = float(np.min(np.abs(freq))) freq_max = float(np.max(np.abs(freq))) d_freq = np.abs(freq_max - freq_min) # ancho de banda if freq_max>0: T_min = 1/freq_max if d_freq>0: # min y max no son iguales if freq_min>0: T_max = 1/d_freq else: # freq_min==0, selecionar otro T_max freq_min = float(np.min(freq[freq>0])) T_max = 1/freq_min else: # min y max son iguales T_max = 1/freq_min T_minmax = [T_min,T_max] return(T_minmax) [T_min,T_max] = periodo_minmax(x_freq) muestras_T = tramos_T + 1 # intervalo de t entre [a,b] en pasos dt a = 0 b = T_max*periodos_graf dt = T_min/tramos_T # tamaño de paso,tramo, muestreo ti = np.arange(a,b+dt,dt) xi_k = [] # muestras de cada señal x for unasenal in x_senales: # x(t) a forma numérica lambda t: if unasenal.has(t): xk = sym.lambdify(t,unasenal) else: # es constante xk = lambda t: unasenal + 0*t xki = xk(ti) # evalúa en intervalo xi_k.append(np.copy(xki)) # graficar fig_x = plt.figure() graf_x = fig_x.add_subplot() for i in range(0,x_conteo,1): color_i = _graf_lineacolor_i(i) graf_x.plot(ti,xi_k[i], color=color_i, label=x_etiqueta[i]) graf_x.axhline(0,color='black') if x_ceros[i]!=sym.nan: graf_x.axvline(x_ceros[i],color=color_i, linestyle='dashed') graf_x.set_title('Señales xk(t)') graf_x.set_xlabel('t (segundos)') graf_x.set_ylabel('x_senales') graf_x.grid() graf_x.legend() plt.show()
[ fasores ] [ ejemplo ] [ analítico ] [ algoritmo ] [ gráfica] [ función ]