s1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

Ejercicio: 1Eva2009TII_T2 LTI DT bloques, respuesta impulso y paso

literal a. Respuesta al impulso, o H(s) del diagrama de bloques

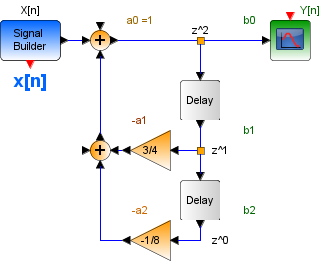
a.1 H[z] Función de transferencia

Referencia: LTI DT – H[z] Diagrama de bloques con "1/z"

Dado que hay dos bloques (1/z) o de retraso , se identifica que los polinomios son de segundo orden (N=2). Los coeficientes de retraso se leen de arriba hacia abajo como a₀,-a₁,-a₂ ordenados en la siguiente tabla:

retraso	adelanto
a₀ = 1	b₀ = 1
a₁ = -(3/4) = -3/4	b₁ = 0
a₂ = -(-1/8) = 1/8	b₂ = 0

Se aplica lo mismo para los coeficientes de adelanto y se completa el modelo para los polinomios del numerador y denominador:

H[z] = \frac{b_0 z^N +b_1 z^{N-1} + \text{ ... } + b_{N-1} z + b_N}{z^N + a_1 z^{N-1} +\text{ ... } + a_{N-1}z +a_N}

H[z] = \frac{z^2}{z^2 - \frac{3}{4} z+\frac{1}{8}}

a.2 H[z] en fracciones parciales

fracciones parciales modificadas,

\frac{H[z]}{z} = \Big( \frac{1}{z} \Big) \frac{z^2}{z^2 - \frac{3}{4} z+\frac{1}{8}} = \frac{z}{z^2 - \frac{3}{4} z+\frac{1}{8}}

El polinomio del denominador es:

Q[z] = z^2 - \frac{3}{4} z+\frac{1}{8}

con raíces en 1/4 y 1/2

con lo que se obtiene la expresión para usar el método de "cubrir" de Heaviside

\frac{H[z]}{z} = \frac{z}{(z-1/4)(z-1/2)}= \frac{k_1}{z-1/4}+ \frac{k_2}{z-1/2}

k_1 = \frac{z}{\cancel{(z-1/4)}(z-1/2)}\Big|_{z=1/4} = \frac{1/4}{(1/4-1/2)} = -1

k_2 = \frac{z}{(z-1/4)\cancel{(z-1/2)}}\Big|_{z=1/2} = \frac{1/2}{(1/2-1/4)} = 2

\frac{H[z]}{z} = \frac{-1}{z-1/4}+ \frac{2}{z-1/2}

fracciones parciales

H[z] = \frac{-z}{z-1/4}+ \frac{2z}{z-1/2}

Revisando el resultado con el algoritmo en Python:

 Hz:
          2        
         z         
───────────────────
 2                 
z  - 0.75⋅z + 0.125
fracciones parciales z:
     z         2⋅z  
- ──────── + ───────
  z - 0.25   z - 0.5

polos: {0.250000000000000: 1, 0.500000000000000: 1}
ceros: {0: 2}
h[n]:
⎛      n        n⎞     
⎝- 0.25  + 2⋅0.5 ⎠⋅θ(n)

Se obtiene h[n] usando la tabla de transformadas z

     z         2⋅z  
- ──────── + ───────
  z - 0.25   z - 0.5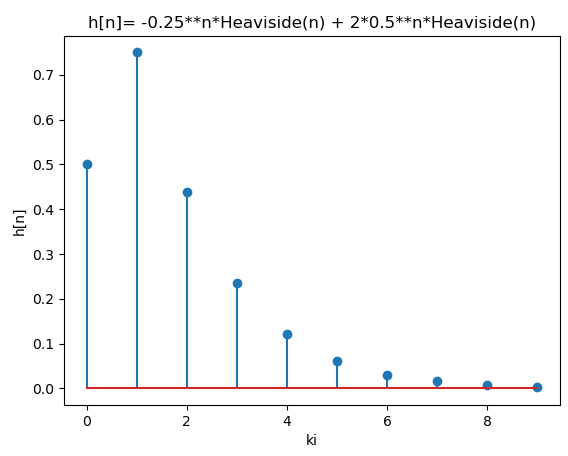

h[n] = - \Big(\frac{1}{4}\Big)^n \mu[n]+2\Big( \frac{1}{2} \Big)^n \mu[n]

a.3. Estabilidad del sistema

Los polos son menores que un radio de 1.

La ROC para el primer polo |z|>1/4 y para el segundo polo es |z|>1/2

Observaciones:

Las raíces características o frecuencias naturales del sistema se encuentran dentro del círculo de radio unitario. El sistema es asintóticamente estable, que implica que es BIBO estable.

h[n] no es de la forma k δ[n], por lo que el sistema global es con memoria.

a.4 Instrucciones con Python

Usando los algoritmo de la sección LTID Transformada z – X[z] Fracciones parciales modificadas con Python se adapta para el ejercicio

# Transformada z- Fracciones parciales
# Polos únicos, repetidos y complejos
# Lathi Ejercicio 5.3a pdf495
# https://blog.espol.edu.ec/algoritmos101/senales/ss-unidades/ss-unidad-7/
import numpy as np
import sympy as sym
import telg1001 as fcnm
  
# INGRESO
z = sym.Symbol('z')
n = sym.Symbol('n')
 
Pz = z**2
Qz = z**2-(3/4)*z+1/8

Hz = Pz/Qz
 
muestras = 10 #para la gráfica
f_nombre = 'H'    # nombre de función[z]: H,X,Y, etc
  
# PROCEDIMIENTO 
Fz  = fcnm.apart_z(Hz)
Qs2 = fcnm.Q_cuad_z_parametros(Fz)
[Q_polos,P_ceros] = fcnm.busca_polosceros_z(Fz)
hn = fcnm.inverse_z_transform(Fz,z,n)
 
# SALIDA
print('\n Hz:')
sym.pprint(Hz)
print('\n fracciones parciales z:')
sym.pprint(Fz)
print('\n polos:',Q_polos)
print('ceros:',P_ceros)
if len(Qs2)>0:
    print('\n parametros cuadraticos: ')
    for unterm in Qs2:
        print(unterm,':')
        for unparam in Qs2[unterm]:
            print(unparam,':',Qs2[unterm][unparam])
print('\nh[n]:')
sym.pprint(hn)
 
# GRAFICA ------------------
import matplotlib.pyplot as plt
# grafica de polos y zeros
fig_ROC = fcnm.graficar_Fz_polos(Hz,Q_polos,P_ceros,
                      muestras,f_nombre)
#plt.show()
 
# grafica F[n]
fn = sym.lambdify(n,hn)
ki = np.arange(0,muestras,1)
fi = fn(ki)
fig_fn, graf_fn = plt.subplots()
plt.stem(ki,fi)
plt.xlabel('ki')
plt.ylabel(f_nombre.lower()+'[n]')
untitulo = r''+f_nombre.lower()+'[n]=$'
untitulo = untitulo+str(sym.latex(hn))+'$'
plt.title(untitulo)
plt.show()

literal b. La respuesta de paso s[n]

La señal de entrada será x[n] = μ[n], con transformada z de:

X[z] = \frac{z}{z-1}

b.1 Y[z] ante entrada X[z] y con función de transferencia H[z]

Usando el resultado de la respuesta al impulso,

H[z] = \frac{-z}{z-1/4}+ \frac{2z}{z-1/2}

La salida Y[n] del sistema será:

Y[z] = X[z] H[z] = \frac{z}{z-1} \Bigg[ \frac{-z}{z-1/4} + \frac{2z}{z-1/2} \Bigg]

b.2 Y[z] en fracciones parciales

Fracciones parciales modificadas

\frac{Y[z]}{z} = \frac{1}{z-1} \Bigg[ \frac{-z}{z-1/4} + \frac{2z}{z-1/2} \Bigg]

\frac{Y[z]}{z} = \frac{1}{(z-1)} \frac{-z}{z-1/4} + \frac{1}{(z-1)}\frac{2z}{z-1/2}

La expresión se puede operar por partes:

\frac{-z}{(z-1)(z-1/4)} = \frac{k_1}{z-1} + \frac{k_2}{z-1/4}

k_1 = \frac{-z}{\cancel{(z-1)}(z-1/4)} \Big|_{z=1} = \frac{-1}{(1-1/4)}=-\frac{4}{3}

k_2 = \frac{-z}{(z-1)\cancel{(z-1/4)}} \Big|_{z=1/4} = \frac{-1/4}{(1/4-1)} = \frac{1}{3}

y la segunda parte,

\frac{2z}{(z-1)(z-1/2)} = \frac{k_3}{z-1} + \frac{k_4}{z-1/2}

k_3 = \frac{2z}{\cancel{(z-1)}(z-1/2)} \Big|_{z=1} = \frac{2(1)}{1-1/2} = 4

k_4 = \frac{2z}{(z-1)\cancel{(z-1/2)}} \Big|_{z=1/2} = \frac{2(1/2)}{1/2-1} = -2

Uniendo las partes de fracciones parciales modificadas se tiene:

\frac{Y[z]}{z} = \frac{-4/3}{z-1} + \frac{1/3}{z-1/4} + \frac{4}{z-1}+\frac{-2}{z-1/2}

restaurando las fracciones parciales

Y[z] = \frac{8}{3}\frac{z}{z-1} + \frac{1}{3}\frac{z}{z-1/4} -2\frac{z}{z-1/2}

Usando la tabla de transformadas z

y[n] = \frac{8}{3}\mu [n] + \frac{1}{3}\Big( \frac{1}{4}\Big)^n \mu [n] -2 \Big(\frac{1}{2}\Big) ^n \mu[n]

Usando el algoritmo en Python, se tiene:

 Yz:
              3             
             z              
----------------------------
(z - 1)*(z - 0.5)*(z - 0.25)

 Yz/z:
                 2                
                z                 
----------------------------------
     3         2                  
1.0*z  - 1.75*z  + 0.875*z - 0.125

 Yz/z.apart:
0.333333333333333       2.0       2.66666666666667
----------------- - ----------- + ----------------
   1.0*z - 0.25     1.0*z - 0.5        z - 1      

 Yz = (Yz/z)*z
0.333333333333333*z      2.0*z      2.66666666666667*z
------------------- - ----------- + ------------------
    1.0*z - 0.25      1.0*z - 0.5         z - 1       

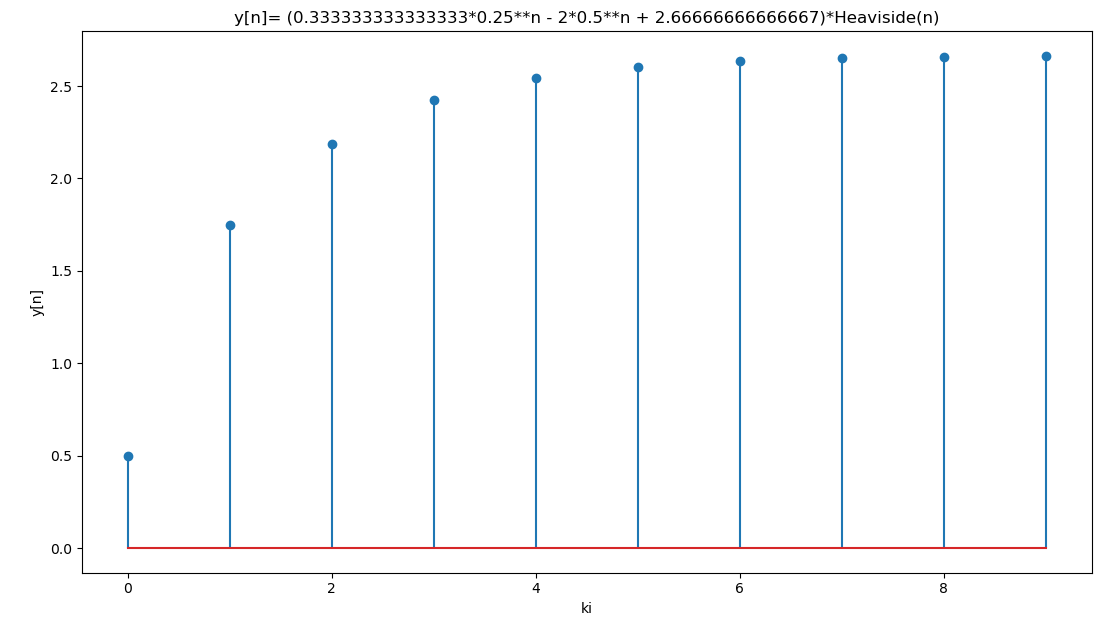
 polos:  {0.2500: 1, 0.5000: 1, 1.0000: 1}

gráfica de salida y[n]