Ejercicio: 1Eva2012TI_T1 LTI CT Polos y ceros de H(s) con respuesta DC conocida
Se revisan los polos y ceros para escribir la función de transferencia,
H(s) = \frac{(s-ceros_0)(s-ceros_1)}{(s-polo_0)(s-polo_1)} H(s) = \frac{(s-(-1.5j))(s-(1.5j))}{(s-(-1+0.5j))(s-(-1-0.5j))}
tomando el modelo proporcionado de la ecuación, se compara para encontrar los valores de las variables
H(s) = \frac{k (s^2 + b_1 s + b_2)}{s^2 + a_1 s + a_2}k = 1, b1=0, b2=2.25, a1=2, a2=1.25
Separando en fracciones parciales, dado que el grado M del numerador y grado N denominador son iguales, ganancia el coeficiente del término de mayor grado del numerador. Lo mismo que se obtiene al dividir el numerador y denominador por s2 y hacer s→∞
H(s) = \frac{1+\frac{2.25}{s^2}}{1+2\frac{1}{s}+\frac{1.25}{s^2}} \Big|_{s=\infty} =1 H(s) = 1+\frac{k_1s+k_2}{s^2+2s+1.25} H(s) = \frac{s^2+2s+1.25+k_1s+k_2}{s^2+2s+1.25} H(s) = \frac{s^2+(2+k_1)s+(1.25+k_2)}{s^2+2s+1.25}con lo que 2+k1=0, entonces k1=-2,
también 1.25+k2=2.25, entonces K2 = 1
con lo que se obtiene,
H(s) = 1+\frac{-2s +1}{s^2 + 2 s + 1.25}los polos se encuentran sobre el lado izquierdo del plano s, por lo que el sistema es asintoticamente estable
Observe que para H(s) el grado del polinomio el numerador P de H(s) es igual al grado del denominador Q. por lo que M=N. por lo que se considera un función impropia (Lathi 4.3b p339, 4.2 p359). Se genera una respuesta impulso por el valor de la constante 1 que se obtiene al usar fracciones parciales.
Para la transformada inversa, para el término cuadrático, en la tabla de transformadas de Laplace se identifica el caso 12c:
\frac{As+B}{s^2+2as+c} donde A=-2, B=1,a=1,c=1.25
El valor b = \sqrt{c-a^2} se calcula como:
b = \sqrt{1.25-(1)^2} = \frac{1}{2} r = \sqrt{\frac{A^2 c +B^2 -2ABa}{c-a^2}} r = \sqrt{\frac{(-2)^2 (1.25) +(1)^2 -2(-2)(1)(1)}{1.25-(-2)^2}} =\sqrt{\frac{10}{1/4}} = 6.3245 \theta = \tan ^{-1} \Big( \frac{Aa-B}{A\sqrt{c-a^2}}\Big) \theta = \tan ^{-1} \Big( \frac{(-2)(1)-(1)}{(-2)\sqrt{1.25-(1)^2}}\Big)\tan ^{-1}(\frac{-3}{-2(1/2)} = 1.2490h(t) = δ(t) + re-atcos (bt+θ) μ(t)
h(t) = δ(t) + 6.3245e-tcos (t/2+1.2490) μ(t)
Algoritmo en Python
A partir del algoritmo H(s) polos y estabilidad
Para el bloque de ingreso se debe mantener los coeficientes como números enteros o racionales. Recordando que los algoritmos de Sympy para transformadas de Laplace (hasta versión 1.11) se encuentran escritos para el dominio de los enteros y racionales ('ZZ'), por lo que los datos se ingresan como:
k1 = sym.Rational(2.25).limit_denominator(100)
k2 = sym.Rational(1.25).limit_denominator(100)
Hs = (s**2+k1)/(s**2+2*s+k2)con el resultado mostrado,
H:
2 9
s + ─
4
────────────
2 5
s + 2⋅s + ─
4
H_fp:
4⋅(2⋅s - 1)
- ────────────── + 1
2
4⋅s + 8⋅s + 5
Q_polos : {-1 - I/2: 1, -1 + I/2: 1}
P_ceros : {-3*I/2: 1, 3*I/2: 1}
n_polos_real : 0
n_polos_imag : 2
enRHP : 0
unicos : 0
repetidos : 0
asintota : estable
h(t):
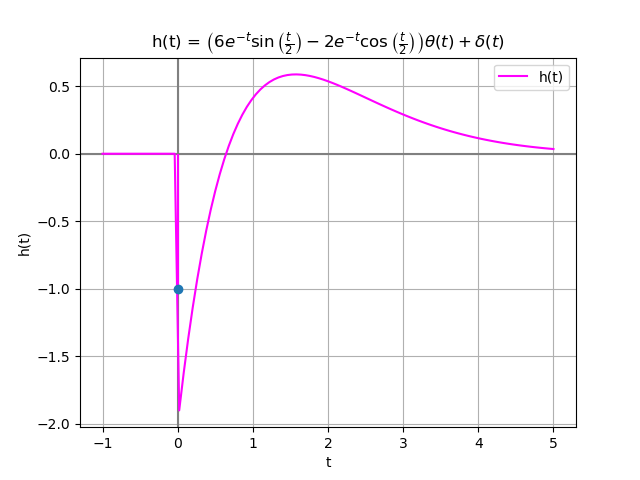
-t ⎛t⎞ -t ⎛t⎞
δ(t) + 6⋅ℯ ⋅sin⎜─⎟⋅θ(t) - 2⋅ℯ ⋅cos⎜─⎟⋅θ(t)
⎝2⎠ ⎝2⎠ Con gráficas de H(s) y polos

gráfica de h(t)
Algoritmo en Python
Usando los bloques desarrollados en la y las funciones resumidas como telg1001.py que pueden ser usados en cada pregunta.
H(s) - polos y Estabilidad del sistema con Sympy-Python
# Estabilidad del sistema, H(s) respuesta al impulso
# Polos y ceros de funcion de transferencia H(s)
# Ps es numerador, Qs es denominador
import sympy as sym
import telg1001 as fcnm
# INGRESO
s = sym.Symbol('s')
t = sym.Symbol('t',real=True)
# H(s) y estabilidad
k1 = sym.Rational(2.25).limit_denominator(100)
k2 = sym.Rational(1.25).limit_denominator(100)
Hs = (s**2+k1)/(s**2+2*s+k2)
#Hs = (s**2+2.25)/(s**2+2*s+1.25)
# condiciones iniciales, [y'(0),y(0)] orden descendente
t0 = 0
cond_inicio = [0, 0] # estado cero no se usan
# Grafica, intervalo tiempo [t_a,t_b]
t_a = -1 ; t_b = 5
muestras = 101 # 51 resolucion grafica
# PROCEDIMIENTO
Hs_fp = fcnm.apart_s(Hs)
polosceros = fcnm.busca_polosceros(Hs_fp)
P_ceros = polosceros['P_ceros']
Q_polos = polosceros['Q_polos']
def estabilidad_asintotica_s(Q_polos, casi_cero=1e-8):
''' Analiza estabilidad asintotica con Q_raiz
Separa parte real e imaginaria de raices
casicero es la tolerancia para considerar cero
'''
# Separa parte real e imaginaria de raices
cuenta_real = 0; cuenta_imag = 0
unicos = 0 ; repetidos = 0 ; enRHP = 0
for raiz in Q_polos:
[r_real,r_imag] = raiz.as_real_imag()
if abs(r_real)>casi_cero and abs(r_imag)<casi_cero :
cuenta_real = cuenta_real+1
# para estabilidad asintotica
conteo = Q_polos[raiz]
if conteo==1 and r_real==0 and abs(r_imag)>0:
unicos = unicos + 1
if conteo>1 and r_real==0 and abs(r_imag)>0:
repetidos = repetidos + 1
if r_real>0:
enRHP = enRHP + 1
cuenta_imag = len(Q_polos)-cuenta_real
# Revisa lado derecho del plano RHP
asintota = ""
if enRHP==0:
asintota = 'estable'
if enRHP>0 or repetidos>0:
asintota = 'inestable'
if enRHP==0 and unicos>0:
asintota = 'marginalmente estable'
estable = {'n_polos_real': cuenta_real,
'n_polos_imag': cuenta_imag,
'enRHP' : enRHP,
'unicos' : unicos,
'repetidos' : repetidos,
'asintota' : asintota,}
return(estable)
estable = estabilidad_asintotica_s(Q_polos)
# h(t) desde H_fp(s) con inversa Laplace
ht = 0*t
term_suma = sym.Add.make_args(Hs_fp.expand())
for term_k in term_suma:
ht_k = sym.inverse_laplace_transform(term_k,s,t)
ht = ht +ht_k
ht = sym.expand(ht,t) # terminos suma
# SALIDA
print('H:')
sym.pprint(Hs)
print('H_fp:')
sym.pprint(Hs_fp)
fcnm.print_resultado_dict(polosceros)
fcnm.print_resultado_dict(estable)
print('\n h(t): ')
sym.pprint(ht)
# GRAFICA -----------
import matplotlib.pyplot as plt
muestras_H = 161
fig_Hs = fcnm.graficar_Fs(Hs_fp,Q_polos,P_ceros,
muestras=muestras_H,
f_nombre='H',solopolos=True)
figura_h = fcnm.graficar_ft(ht,t_a,t_b,f_nombre='h')
plt.show()
.