1.7 Espectro - Operaciones en dominio de tiempo y frecuencia

1. Operaciones en dominio de tiempo y frecuencia

Referencia: McClellan 3.3 p81

Uno de los beneficios de uso del espectro de frecuencias es que las operaciones sobre x(t) se muestran como resultados simples en la gráfica de espectro. Estos cambios relacionados en el dominio de t y f se denominan propiedades de la representación espectral. Para los ejemplos se usará el algoritmo de producto de sinusoides.

Escala o sumar 'c'

2. Escalar o sumar con una constante

Referencia: McClellan 3.3.1 y 3.3.2 p81

Multiplicar una señal por un factor 'c' constante cambia la escala de amplitud en el espectro por el mismo factor 'c', pero deja las frecuencias sin cambios.

c x(t)= c \sum_{k=−M}^M a_k e^{j2\pi f_kt} = \sum_{k=−M}^M (c a_k) e^{j 2 \pi f_k t}

Sumar una constante a una señal x(t)+c, cambia la amplitud compleja de solo del componente constante o frecuencia f=0

x(t)+c=\sum_{f \neq 0} a_ke^{j2 \pi f_k t} + \left[ a_0 e^{j2 \pi (0) t} + c \right]

2.1 Ejemplo

Para la señal x(t) mostrada

x(t) = \frac{2}{3}​ + 6 \cos(6\pi t − \pi /3 ) + 4 \cos(14\pi t + \pi/4)

realizar las operaciones

y(t)=2x(t)+6

La amplitud de las señales en f=±3 y ±7 se duplican en el factor 2, El valor de la constante a la frecuencia cero, también se duplica por el factor 2 y se añade la constante 6 dando como resultado 2(1.5) +6 = 9

2.2 Resultado con algoritmo

Ingreso

# INGRESO
x1 = 3/2 + 6*sym.cos(6*pi*t - pi/3) + 4*sym.cos(14*pi*t + pi/4)
x2 = 2*x1
x3 = 6
x4 = x2+x3

# Para espectro de frecuencias y fasores
x_senales = [x1,x2,x3,x4]
x_etiqueta = ['x1(t)','(2)x1(t)','x3(t)','(2)x1(t)+x3(t)']

Resultado

senal:   6*sin(6*pi*t + pi/6) + 4*cos(14*pi*t + pi/4) + 1.5
  espectro:
   freq : [-7. -3.  0.  3.  7.]
   ampl : [2.  3.  1.5 3.  2. ]
   fase : [-pi/4 pi/3 0 -pi/3 pi/4]
   etiq : ['$2$$ e^j(- \\frac{\\pi}{4})$' '$3$$ e^j(\\frac{\\pi}{3})$' '$1.5$'
 '$3$$ e^j(- \\frac{\\pi}{3})$' '$2$$ e^j(\\frac{\\pi}{4})$']
   x_expand : 6*sin(6*pi*t + pi/6) + 4*cos(14*pi*t + pi/4) + 1.5
   freq_max : 7.0
   freq_min : 3.0
   BW : 4.0
senal:   12*sin(6*pi*t + pi/6) + 8*cos(14*pi*t + pi/4) + 3.0
  espectro:
   freq : [-7. -3.  0.  3.  7.]
   ampl : [4 6 3 6 4]
   fase : [-pi/4 pi/3 0 -pi/3 pi/4]
   etiq : ['$4$$ e^j(- \\frac{\\pi}{4})$' '$6$$ e^j(\\frac{\\pi}{3})$' '$3$'
 '$6$$ e^j(- \\frac{\\pi}{3})$' '$4$$ e^j(\\frac{\\pi}{4})$']
   x_expand : 12*sin(6*pi*t + pi/6) + 8*cos(14*pi*t + pi/4) + 3
   freq_max : 7.0
   freq_min : 3.0
   BW : 4.0
senal:   6
  espectro:
   freq : [0.]
   ampl : [6]
   fase : [0]
   etiq : ['$6$']
   x_expand : 6
   freq_max : 0.0
   freq_min : 0
   BW : 0.0
senal:   12*sin(6*pi*t + pi/6) + 8*cos(14*pi*t + pi/4) + 9.0
  espectro:
   freq : [-7. -3.  0.  3.  7.]
   ampl : [4 6 9 6 4]
   fase : [-pi/4 pi/3 0 -pi/3 pi/4]
   etiq : ['$4$$ e^j(- \\frac{\\pi}{4})$' '$6$$ e^j(\\frac{\\pi}{3})$' '$9$'
 '$6$$ e^j(- \\frac{\\pi}{3})$' '$4$$ e^j(\\frac{\\pi}{4})$']
   x_expand : 12*sin(6*pi*t + pi/6) + 8*cos(14*pi*t + pi/4) + 9
   freq_max : 7.0
   freq_min : 3.0
   BW : 4.0

gráfica de espectro de frecuencias

3. Desplazamiento en tiempo o multiplicar por exponencial complejo

Referencia: McClellan 3.3.3 p84

Para desplazamiento en el tiempo, las frecuencias no cambia, solo hay cambio de fase en las amplitudes complejas del espectro.

y(t) = x (t−\tau_d) \leftrightarrow b_k = a_k e^{−j2 \pi f_k \tau_d}

dado que

y(t) = x(t − \tau_d) =\sum_k a_k e^{−j2 \pi f_k (t−\tau_d)} = \sum_k \left(a_k e^{−j2 \pi f_k \tau_d} \right) e^{j 2 \pi f_k t}

3.1 Ejemplo

Considere x(t) con un retraso τ_d que es 1/4 de su periodo.

x(t) = 6 \cos⁡(250 \pi t)

T=\frac{1}{125}

\tau_d=\frac{T}{4} =\left(\frac{1}{125} \right) \frac{1}{4}=\frac{1}{500} = 0.002

e^{−j 250\pi (0.002)} = e^{−j0.5\pi} = −j

x(t−0.002)=6\sin⁡(250 \pi t)

3.2 Resultado con algoritmo

Ingreso

# INGRESO
x0 = 6*sym.cos(250*pi*t)
x1 = x0.subs(t,t-0.002)

# Para espectro de frecuencias y fasores
x_senales = [x0,x1]
x_etiqueta = ['x(t)','x(t-0.002)']

Resultado

x_senales: 
senal:   6*cos(250*pi*t)
  espectro:
   freq : [-125.  125.]
   ampl : [3 3]
   fase : [0 0]
   etiq : ['$3$' '$3$']
   x_expand : 6*cos(250*pi*t)
   freq_max : 125.0
   freq_min : 125.0
   BW : 0.0
senal:   6*cos(pi*(250*t - 0.5))
  espectro:
   freq : [-125.  125.]
   ampl : [3 3]
   fase : [0.5*pi -0.5*pi]
   etiq : ['$3$$ e^j(0.5 \\pi)$' '$3$$ e^j(- 0.5 \\pi)$']
   x_expand : 3*I*cos(250*pi*t) + 3*I*cos(250*pi*t - 1.0*pi) + 6*cos(250*pi*t - 0.5*pi)
   freq_max : 125.0
   freq_min : 125.0
   BW : 0.0

gráfica de espectro de frecuencias

4. Diferenciación en tiempo - derivar

Referencia: McClellan 3.3.4 p84

La derivada de una señal x(t) no realiza cambios en las frecuencias, las amplitudes en el espectro de frecuencia se modifican como

y(t) = \frac{d}{dt} x(t) \leftrightarrow b_k=(j 2 \pi f_k) a_k

dado que

y(t) = \frac{d}{dt} x(t)= \sum_k a_k \frac{d}{dt} e^{j2\pi f_k t} =\sum_k \left( (j2 \pi f_k) a_k \right) e^{j2 \pi f_k t}

4.1 Ejemplo

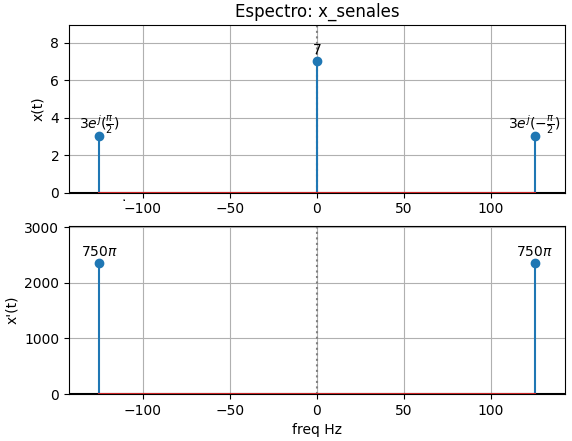
Derivar x(t) que tiene sin() y una constante.

x(t)=7+6 \cos⁡(250 \pi t)

La frecuencia f=0 tiene magnitud 7 que es (j 2 π (0)) = 0 que se elimina de la expresión. En la frecuencia de 125 Hz el término se multiplica por (j 2 π (125))

(j2 \pi (125))(−3j) = 750\pi

\frac{d}{dt} x(t)=1500 \pi \cos⁡(250 \pi t)

4.2 Resultados con el algoritmo

Ingreso

# INGRESO
x0 = 7 + 6*sym.sin(250*pi*t)
x1 = sym.diff(x0,t)

# Para espectro de frecuencias y fasores
x_senales = [x0,x1]
x_etiqueta = ['x(t)',"x'(t)"]

Resultado

x_senales: 
senal:   6*cos(250*pi*t)
  espectro:
   freq : [-125.  125.]
   ampl : [3 3]
   fase : [0 0]
   etiq : ['$3$' '$3$']
   x_expand : 6*cos(250*pi*t)
   freq_max : 125.0
   freq_min : 125.0
   BW : 0.0
senal:   6*cos(pi*(250*t - 0.5))
  espectro:
   freq : [-125.  125.]
   ampl : [3 3]
   fase : [0.5*pi -0.5*pi]
   etiq : ['$3$$ e^j(0.5 \\pi)$' '$3$$ e^j(- 0.5 \\pi)$']
   x_expand : 3*I*cos(250*pi*t) + 3*I*cos(250*pi*t - 1.0*pi) + 6*cos(250*pi*t - 0.5*pi)
   freq_max : 125.0
   freq_min : 125.0
   BW : 0.0
>>>

gráfica de espectro de frecuencias

5. Desplazamiento de frecuencia

Referencia: McClellan 3.3.5 p85

Multiplicar una señal x(t) por una sinusoide o una exponencial compleja tiene como resultado que las frecuencias en el espectro se desplazan.

y(t)=x(t) A \cos⁡(2 \pi f_c t+ \Phi )

= x(t)\frac{1}{2} A e^{j \Phi } e^{j 2 \pi f_c t} + x(t)\frac{1}{2} A e^{−j\Phi} e^{−j2 \pi f_c t} [latex]</p> <p>que es el resultado observado en el producto de sinusoides y tema tratado para AM</p> <p>[latex display="true"] y(t)=A e^{j \phi} e^{j2 \pi f_c t}\sum_k a_k e^{j 2\pi f_k t}

y(t)=\sum_k \left( a_k A e^{j\Phi}\right) e^{j2\pi (f_k+f_c)t}

Que se interpreta en el espectro de frecuencias, cada frecuencia en x(t) se desplaza por f_c, suponiendo que f_c>0. Todas las amplitudes complejas se multiplican por la amplitud compleja del exponencial complejo.

5.1 Ejemplo

Para una señal x(t) con varios componentes mostrada en la gráfica de espectro de frecuencias, añadir a la gráfica los resultados de las operaciones indicadas:

x_1(t)= x(t) \cos⁡(2\pi 9 t)

x_1(t)= x(t) \sin⁡(2\pi 9t)

Siendo

x(t) = 8 + 4 \cos⁡(2\pi t) + 4 \cos⁡(2\pi(2)t) + 12 \cos⁡(2 \pi (3)t + \pi/2)

5.2 Resultados con el algoritmo

Ingreso

# INGRESO
x0 = 8 + 4*sym.cos(DosPi*t) + 4*sym.cos(DosPi*2*t)+ 12*sym.cos(DosPi*3*t + pi/2)
x1 = x0*sym.cos(DosPi*9*t)
x2 = x0*sym.sin(DosPi*9*t)

# Para espectro de frecuencias y fasores
x_senales = [x0,x1,x2]
x_etiqueta = ['x(t)','x(t)*cos(2*pi*9*t)','x(t)*sin(2*pi*9*t)']

Resultado

x_senales: 
senal:   8 - 12*sin(3*t*(2*pi)) + 4*cos(t*(2*pi)) + 4*cos(2*t*(2*pi))
  espectro:
   freq : [-3. -2. -1.  0.  1.  2.  3.]
   ampl : [6 2 2 8 2 2 6]
   fase : [-pi/2 0 0 0 0 0 pi/2]
   etiq : ['$6$$ e^j(- \\frac{\\pi}{2})$' '$2$' '$2$' '$8$' '$2$' '$2$'
 '$6$$ e^j(\\frac{\\pi}{2})$']
   x_expand : -6*I*(-I*sin(6*pi*t) + cos(6*pi*t)) + 6*I*(I*sin(6*pi*t) + cos(6*pi*t)) + 4*cos(2*pi*t) + 4*cos(4*pi*t) + 8
   freq_max : 3.0
   freq_min : 1.0
   BW : 2.0
senal:   (8 - 12*sin(3*t*(2*pi)) + 4*cos(t*(2*pi)) + 4*cos(2*t*(2*pi)))*cos(9*t*(2*pi))
  espectro:
   freq : [-12. -11. -10.  -9.  -8.  -7.  -6.   6.   7.   8.   9.  10.  11.  12.]
   ampl : [3 1 1 4 1 1 3 3 1 1 4 1 1 3]
   fase : [-pi/2 0 0 0 0 0 pi/2 -pi/2 0 0 0 0 0 pi/2]
   etiq : ['$3$$ e^j(- \\frac{\\pi}{2})$' '$1$' '$1$' '$4$' '$1$' '$1$'
 '$3$$ e^j(\\frac{\\pi}{2})$' '$3$$ e^j(- \\frac{\\pi}{2})$' '$1$' '$1$'
 '$4$' '$1$' '$1$' '$3$$ e^j(\\frac{\\pi}{2})$']
   x_expand : 3*I*(-I*sin(12*pi*t) + cos(12*pi*t)) - 3*I*(I*sin(12*pi*t) + cos(12*pi*t)) - 3*I*(-I*sin(24*pi*t) + cos(24*pi*t)) + 3*I*(I*sin(24*pi*t) + cos(24*pi*t)) + 8*cos(18*pi*t)
   freq_max : 12.0
   freq_min : 6.0
   BW : 6.0
senal:   (8 - 12*sin(3*t*(2*pi)) + 4*cos(t*(2*pi)) + 4*cos(2*t*(2*pi)))*sin(9*t*(2*pi))
  espectro:
   freq : [-12. -11. -10.  -9.  -8.  -7.  -6.   6.   7.   8.   9.  10.  11.  12.]
   ampl : [3 1 1 4 1 1 3 3 1 1 4 1 1 3]
   fase : [0 pi/2 pi/2 pi/2 pi/2 pi/2 pi pi -pi/2 -pi/2 -pi/2 -pi/2 -pi/2 0]
   etiq : ['$3$' '$1$$ e^j(\\frac{\\pi}{2})$' '$1$$ e^j(\\frac{\\pi}{2})$'
 '$4$$ e^j(\\frac{\\pi}{2})$' '$1$$ e^j(\\frac{\\pi}{2})$'
 '$1$$ e^j(\\frac{\\pi}{2})$' '$3$$ e^j(\\pi)$' '$3$$ e^j(\\pi)$'
 '$1$$ e^j(- \\frac{\\pi}{2})$' '$1$$ e^j(- \\frac{\\pi}{2})$'
 '$4$$ e^j(- \\frac{\\pi}{2})$' '$1$$ e^j(- \\frac{\\pi}{2})$'
 '$1$$ e^j(- \\frac{\\pi}{2})$' '$3$']
   x_expand : I*(-I*sin(14*pi*t) + cos(14*pi*t)) - I*(I*sin(14*pi*t) + cos(14*pi*t)) + I*(-I*sin(16*pi*t) + cos(16*pi*t)) - I*(I*sin(16*pi*t) + cos(16*pi*t)) + 4*I*(-I*sin(18*pi*t) + cos(18*pi*t)) - 4*I*(I*sin(18*pi*t) + cos(18*pi*t)) + I*(-I*sin(20*pi*t) + cos(20*pi*t)) - I*(I*sin(20*pi*t) + cos(20*pi*t)) + I*(-I*sin(22*pi*t) + cos(22*pi*t)) - I*(I*sin(22*pi*t) + cos(22*pi*t)) - 6*cos(12*pi*t) + 6*cos(24*pi*t)
   freq_max : 12.0
   freq_min : 6.0
   BW : 6.0

gráfica de espectro de frecuencias

6. Algoritmo en Python

La instrucciones en Python para cada ejercicio a observar en el dominio de la frecuencia requiere actualiar la sección de INGRESO que fué proporcinada en cada sección anterior. El algoritmo se presenta como ejemplo la escala o suma de una constante.

# ejemplo 3-3.1 p82 escala o suma con una constante
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
import telg1034 as dsp

# variables
from telg1034 import t,A,w,f,p,pi,DosPi,I,equivalentes

# INGRESO
x1 = 3/2 + 6*sym.cos(6*pi*t - pi/3) + 4*sym.cos(14*pi*t + pi/4)
x2 = 2*x1
x3 = 6
x4 = x2+x3

# Para espectro de frecuencias y fasores
x_senales = [x1,x2,x3,x4]
x_etiqueta = ['x1(t)','(2)x1(t)','x3(t)','(2)x1(t)+x3(t)']

# PROCEDIMIENTO
x_conteo = len(x_senales)
x_espectro = [] ; freq_max_graf = 1; freq_min_graf = 0
for unasenal in x_senales:
    # operaciones para espectro
    x_term = dsp.x_list_term_Add(unasenal)
    Xe_term = dsp.cos_to_euler_one_term(x_term)
    x_term_expand = dsp.euler_to_cos_list(Xe_term)
    Xe_term_spectr = dsp.cos_spectrum_list(x_term)
    
    # espectro de cada señal
    un_espectro = {}
    freq = Xe_term_spectr['freq']
    ampl = Xe_term_spectr['ampl']
    fase = Xe_term_spectr['fase']
    un_espectro['freq'] = freq
    un_espectro['ampl'] = ampl
    un_espectro['fase'] = fase
    un_espectro['etiq'] = Xe_term_spectr['etiq']
    un_espectro['x_expand'] = x_term_expand
    
    # ancho de banda
    freq_max = float(max(freq))
    if len(freq[freq>0])>0:
        freq_min = float(min(freq[freq>0]))
    else:
        freq_min = 0
    un_espectro['freq_max'] = freq_max
    un_espectro['freq_min'] = freq_min
    freq_centro = (freq_max+freq_min)/2
    un_espectro['BW'] = freq_max-freq_min

    x_espectro.append(un_espectro)
    # freq_max para grafica, eje unificado x_senales
    if freq_max>freq_max_graf:
        freq_max_graf = freq_max

# SALIDA
print('x_senales: ')
for i in range(x_conteo):
    print('senal:  ',x_senales[i])
    print('  espectro:')
    unespectro = x_espectro[i]
    for unparam in unespectro:
        print('  ',unparam,':',unespectro[unparam])

7. Gráfica con Python

# GRAFICAS de espectro de frecuencias ---------
graf_dx = 0.14
fig_espectro = plt.figure()
for i in range(0,x_conteo,1):
    unespectro = x_espectro[i]
    freq = unespectro['freq']
    ampl = unespectro['ampl']
    etiqueta = unespectro['etiq']
    ampl_max = float(max(ampl))
    # grafica
    graf_sub = x_conteo*100+10+i+1
    graf_fasor = fig_espectro.add_subplot(graf_sub)
    if freq_max_graf!=0:
        graf_fasor.set_xlim([-freq_max_graf*(1+graf_dx),
                             freq_max_graf*(1+graf_dx)])
    else:
        graf_fasor.set_xlim([-1,1])
    graf_fasor.set_ylim([0,ampl_max*(1+graf_dx*2)])
    graf_fasor.grid()
    graf_fasor.axhline(0,color='black')
    graf_fasor.axvline(0,linestyle='dotted',color='grey')
    graf_fasor.stem(freq,ampl) # grafica magnitud
    for k in range(0,len(freq),1): # etiquetas de fasor
        plt.annotate(etiqueta[k],xy=(freq[k],ampl[k]),
                     xytext=(0,5),textcoords='offset points',
                     ha='center')
    graf_fasor.set_ylabel(x_etiqueta[i])
    if i == 0:
        graf_fasor.set_title('Espectro: x_senales')
    if i ==(x_conteo-1):
        graf_fasor.set_xlabel('freq Hz')

plt.show()

1.7 Espectro - Operaciones en dominio de tiempo y frecuencia

1. Operaciones en dominio de tiempo y frecuencia

2. Escalar o sumar con una constante

2.1 Ejemplo

2.2 Resultado con algoritmo

3. Desplazamiento en tiempo o multiplicar por exponencial complejo

3.1 Ejemplo

3.2 Resultado con algoritmo

4. Diferenciación en tiempo - derivar

4.1 Ejemplo

4.2 Resultados con el algoritmo

5. Desplazamiento de frecuencia

5.1 Ejemplo

5.2 Resultados con el algoritmo

6. Algoritmo en Python

7. Gráfica con Python

Procesamiento Digital de Señales DSP

Digital Signal Processing