La DFT es una versión discreta del espectro de frecuencias de tipo X(ejω ) que es contínua y conocida como DTFT. Se puede construir pares de DFT haciendo la sustitución ω=(2π/N)/k en un par DTFT
1. DFT de un impulso unitario desplazado
Referencia: McClellan 8.1.2.1 p306. Transformada de Fourier – Señales aperiódicas continuas
Tomando la DFT de x[n] =δ[n], la sumatoria de DFT se simplifica a un término
X[k] = \sum_{n=0}^{N-1} \delta [n] e^{-j(2\pi k/N)n} = \delta [0] e^{-j(2\pi k/N)(0)} + \sum_{n=1}^{N-1} \cancel{\delta [n]} e^{-j(2\pi k/N)n} = \delta [0] (1) + 0 = 1Usando la respuesta anterior, para x[n] = δ[n-nd]m se puede escribir
X[k] = \delta [n_d] e^{-j(2\pi k/N)n_d} = e^{-j\omega n_d} \delta [n-n_d] \leftrightarrow e^{-j\omega n_d}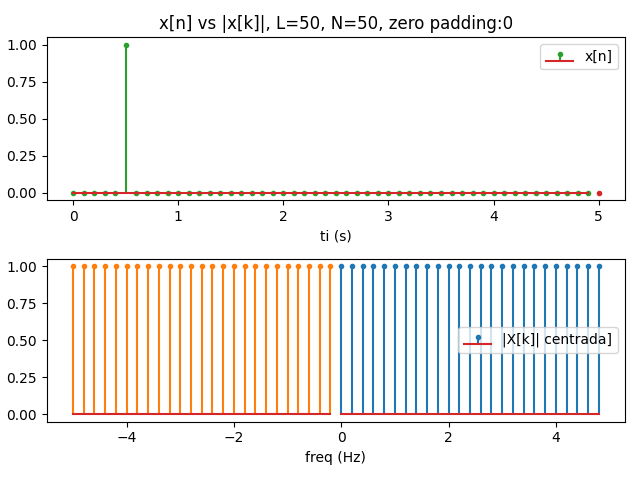
Se crea a partir de una función rectangular con ancho igual al tamaño de paso.
# INGRESO
L = 50 # Tramos en un periodo
# señal es impulso unitario periódico d[n], rectangular ancho "pequeño"
f0 = 0.2 # frecuencia fundamental de señal
ancho = 1/f0/L # ancho del impulso rectangular
n0 = 0.5 # desplazamiento en tiempo
xt = lambda n: np.heaviside(n-n0,1)-np.heaviside(n-n0-ancho,1)
# para DFT
N = 1*L # N par mayor que L, tramos DFT, FFT2. DFT de un pulso rectangular
Referencia: Transformada de Fourier – Señales aperiódicas continuas
Para un pulso rectangular en el domino de tiempo discreto, expresado como:
r [n] = \begin {cases} 1 & 0\leq n \leq L-1 \\ 0 & L \leq n \leq N-1 \end {cases}La DFT tiene un término de la forma
R_L[k] = R_L \Big( e^{j\omega} \Big) = \frac{\sin \Big( \frac{1}{2} L(2\pi k/N)\Big)}{\sin \Big( \frac{1}{2} (2\pi k/N)\Big)} e^{-j(2 \pi k/N)(L-1)/2}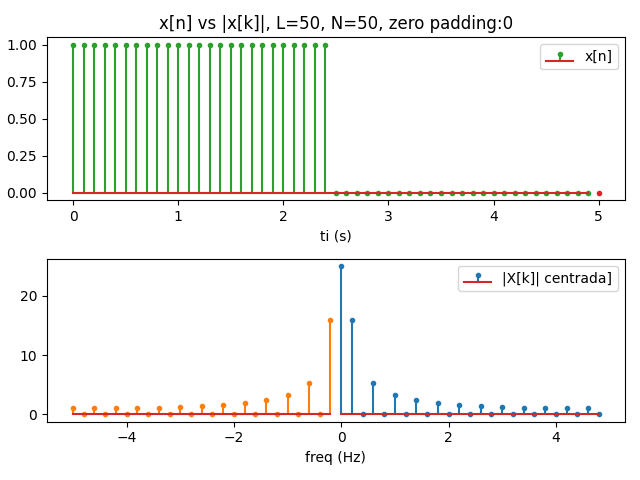
Se crea a partir de una función rectangular con ancho igual a la mitad de un periodo.
# INGRESO
L = 50 # Tramos en un periodo
# señal es rectangular periódico rect[n]
f0 = 0.2 # frecuencia fundamental de señal
ancho = 0.5*(1/f0) # ancho del impulso rectangular
xt = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1)
# para DFT
N = 1*L # N par mayor que L, tramos DFT3. DFT de un exponencial complejo
Una señal exponencial compleja de tamaño finito se expresa como
x [n] = r_L[n] e^{j \omega_0 n}= \begin {cases} e^{j\omega_0 n} & 0\leq n \leq L-1 \\ 0 & L \leq n \leq N-1 \end {cases}La DFT tiene un término de la forma
X[k] = R_L \Big( e^{j\omega-\omega_0} \Big) = \frac{\sin \Big( \frac{1}{2} L(2\pi k/N - \omega_0)\Big)}{\sin \Big( \frac{1}{2} (2\pi k/N- \omega_0)\Big)} e^{-j(2 \pi k/N- \omega_0)(L-1)/2}expresión que también se representa en términos de Dirichlet
X[k] = D_L(2\pi k/N - \omega_0) e^{-j(2 \pi k/N- \omega_0)(L-1)/2}Dado que el exponencial solo contribuye a la fase, el resultado muestra que la magnitud depende solo del termino DL
La DFT es muy simple cuando la frecuencia de la señal exponencial es un múltiplo entero de 2π/N y la cantidad de muestras DFT son iguales a la cantidad de muestras de la señal N=L.
X[k] = N \delta [k-k_0]
Para N=2L, la gráfica adquiere mayor resolución en el dominio de la frecuencia, donde se requiere completar los puntos L para que sean iguales a N y realizar el cálculo de fft.
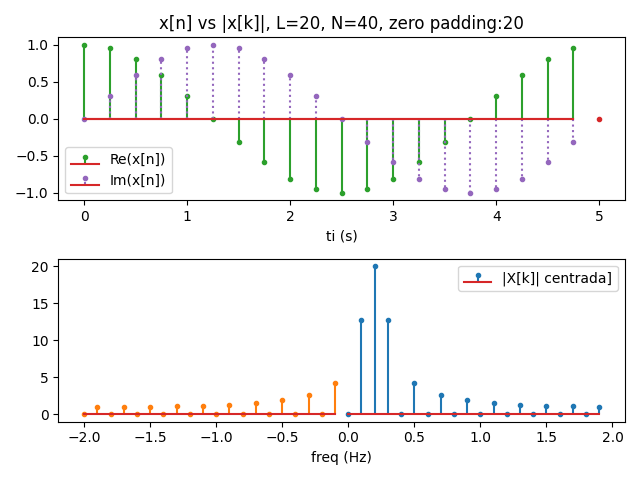
Se crea a partir de una función exponencial multiplicada por una rectangular con ancho igual a un periodo. Para la gráfica se considera solo la parte real de la función.
# INGRESO
L = 20 # Tramos en un periodo
# señal es exponencial complejo periódico
f0 = 0.2 # frecuencia fundamental de señal
ancho = 1*(1/f0) # ancho del impulso rectangular
rect = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1)
xt = lambda t: rect(t)*np.exp(1j*2*np.pi*f0*t)
# para DFT
N = 2*L # N par mayor que L, tramos DFT4. Algoritmo en Python
Se adjunta el algoritmo para los ejercicios, el bloque de ingreso presentado corresponde al ejercicio de exponencial complejo. Para los otros ejercicios actualizar el bloque de INGRESO
# ejemplo 8.1.2.2 p307 DFT x[n] zero-padding
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
L = 20 # Tramos en un periodo
# señal es exponencial complejo periódico
f0 = 0.2 # frecuencia fundamental de señal
ancho = 1*(1/f0) # ancho del impulso rectangular
rect = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1)
xt = lambda t: rect(t)*np.exp(1j*2*np.pi*f0*t)
# para DFT
N = 2*L # N par mayor que L, tramos DFT
# PROCEDIMIENTO
# muestreo de señal x[n]
t0 = 0 ; tn = 1/f0 # intervalo [t0,tn]
dt = (tn-t0)/L
ti = np.arange(t0,tn,dt)
xn = xt(ti)
# verificar que L<=N
if L<=N:
# DFT transformada rapida de Fourier
Xk = np.fft.fft(xn,n=N)
Xkmagn = np.abs(Xk) # para gráfica
Xkfase = np.angle(Xk)
freq_Hz = np.fft.fftfreq(N,dt) # frecuencias en Hz
mitad = int(N/2)
k0 = np.argmax(Xk) # Pico |X[k]|
# SALIDA
if N>=L:
print('k0:',k0,'; i:',mitad+k0)
print('freq_Hz:',freq_Hz[k0],
'; Xk[k0]:',Xk[k0])
print('[ i, freq[ki],|X[k]| ,X[k]]')
kmin = k0-4 ; kmax = k0+4
if kmin<0:
kmin = 0
if kmax>N:
kmax = N
for i in range(kmin,kmax,1):
print([i,freq_Hz[i],Xkmagn[i],Xk[i]])
else:
print('Revisar: L debe ser menor o igual a N')
print('L:',L,'; N:',N)
# GRAFICA
if N>=L:
LN_texto= ', L='+str(L)+', N='+str(N)
zp_texto = 'zero padding:'+str(N-L)
plt.subplot(211)
plt.stem(ti,np.real(xn),label='Re(x[n])',
markerfmt ='C2.',linefmt='C2-')
plt.stem(ti,np.imag(xn),label='Im(x[n])',
markerfmt ='C4.',linefmt='C4:')
plt.stem(L*dt,0,markerfmt ='C3.')
plt.xlabel('ti (s)')
plt.title('x[n] vs |x[k]|'+LN_texto+', '+zp_texto)
plt.legend()
plt.subplot(212)
plt.stem(freq_Hz[0:mitad], Xkmagn[0:mitad],
label='|X[k]| centrada]',
markerfmt ='C0.',linefmt='C0-')
plt.stem(freq_Hz[mitad:], Xkmagn[mitad:],
markerfmt ='C1.',linefmt='C1-')
plt.xlabel('freq (Hz)')
plt.legend()
plt.tight_layout()
plt.show()