1. Periódicidad
Referencia: McClellan 8.3.1 p319
La sumatoria de IDFT también tiene propiedad e periodicidad. Considera evaluar una función en n+N, con n en el intervalo 0≤n≤N-1:
x[n+N] = \frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j(2\pi /N)k(n+N)} = \frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j(2\pi /N)k(n)} \cancel{e^{j(2\pi /N)k(N)} }un factor exponencial se convierte en 1, quedando
= \frac{1}{N}\sum_{k=0}^{N-1} X[k] e^{j(2\pi /N)k(n)} = x[n]1. 1 Ejemplo: IDFT de impulso desplazado
Para una señal de L=N=10 puntos x[n]=δ[n-14] tendrá una DFT:
X[k] = e^{-j(0.2\pi (14)k}El resultado de la IDFT tendrá un valor diferente de cero en n=4.
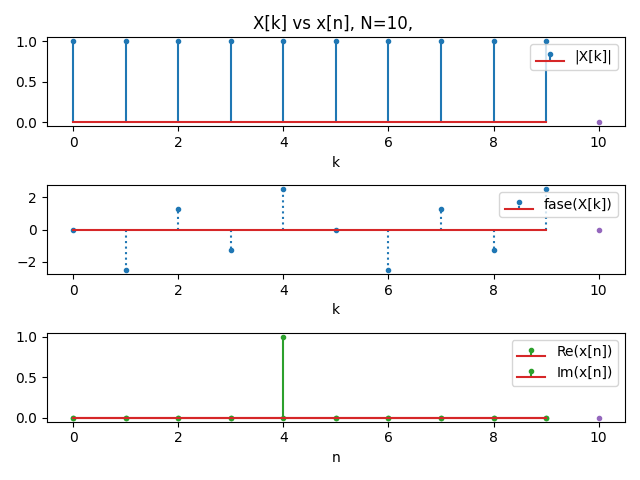
con el algoritmo para no.fft.ifft() se pueden obtener los valores para
N: 10
X[k]:
[ 1. +0.00000000e+00j -0.80901699-5.87785252e-01j
0.30901699+9.51056516e-01j 0.30901699-9.51056516e-01j
-0.80901699+5.87785252e-01j 1. +1.71450552e-15j
-0.80901699-5.87785252e-01j 0.30901699+9.51056516e-01j
0.30901699-9.51056516e-01j -0.80901699+5.87785252e-01j]
Re(x[n]):
[-4.88498131e-16 -7.98670570e-16 -9.76996262e-16 -9.51130884e-16
1.00000000e+00 9.49240686e-16 9.76996262e-16 8.05446317e-16
5.32907052e-16 -4.88554849e-18]
Im(x[n]):
[-7.16727868e-16 -3.76270034e-16 2.39540920e-17 4.01492493e-16
2.23107982e-15 3.94763191e-16 4.54309871e-17 -3.94454259e-16
-7.26484270e-16 -8.82784150e-16]considerando como bloque de ingreso:
# INGRESO
X_k = lambda k: np.exp(-1j*0.2*np.pi*14*k)
N = 10 # Tramos en intervalo
k0 = 0 # inicio de gráfica
2. Propiedad de la Convolución
La convolución en el domino del tiempo se puede desarrollar como una multiplicación en el dominio de la frecuencia.
y[n] = h[n] * x[n] \leftrightarrow Y(e^{j \omega} )= H(e^{j \omega}) X(e^{j \omega})Siendo la DFT una versión discreta de tamaño finito, de la DTFT contínua:
y[n] = \sum_{m=0}^{M-1} h[m] x[n-m]donde se supone que h[n]= 0 fuera del intervalo n= 0, 1, ... , M-1,
x[n]=0 fuera del intervalo n= 0, 1, ... , L-1
h[n] es una secuencia d M puntos y x[n] es una secuencia de L puntos.
obteniendo y[n]
y[n] = \frac{1}{N}\sum_{k=0}^{N-1} Y[k] e^{j(2 \pi /N)kn}2. 1 Ejemplo: Convolución de pulsos
Suponga una señal h[n] compuesta de 16 puntos de los que 6 se encuentran en valor 1 y el resto en cero. La señal x[n] es una señal de pulsos de tamaño 16 puntos, 10 en estado uno, el resto en cero. Considerando que Y[k] = H[k] X[k], use np.fft.fft y np.fft.ifft para mostrar la convolución resultante en el dominio del tiempo.
![ifft convolucion rect X[k] H[k] rect](http://blog.espol.edu.ec/algoritmos101/files/2024/12/ifft_convolucion_rect_X_H_01.png)
k0x: 0 ; i: 8
freq_Hz: 0.0 ; Xk[k0x]: (10+0j)
[ i, freq[ki],|X[k]| ,X[k]]
[0, 0.0, 10.0, (10+0j)]
[1, 0.2, 4.735650251450756, (-0.9238795325112867-4.6446560597607585j)]
[2, 0.4, 1.8477590650225735, (1.7071067811865475-0.7071067811865476j)]
[3, 0.6000000000000001, 0.688811980233627, (-0.38268343236508984-0.5727262301542022j)]
k0h: 0 ; i: 8
freq_Hz: 0.0 ; Hk[k0h]: (6+0j)
[ i, freq[ki],|H[k]| ,H[k]]
[0, 0.0, 6.0, (6+0j)]
[1, 0.2, 4.735650251450756, (2.630986313697834-3.937549278574211j)]
[2, 0.4, 1.8477590650225735, (-0.7071067811865476-1.7071067811865475j)]
[3, 0.6000000000000001, 0.688811980233627, (0.6755766511785423+0.1343805510323453j)]Algoritmo en Python
# ejemplo 8.3.3 p324 DFT convolucion
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
L = 16 # Tramos en un periodo
# señal es rectangular periódico rect[n]
f0 = 0.2 # frecuencia fundamental de señal
ancho = (10/16)*(1/f0) # ancho del impulso rectangular
xt = lambda t: np.heaviside(t,1)-np.heaviside(t-ancho,1)
# señal H es rectangular periódico rect[n]
f0 = 0.2 # frecuencia fundamental de señal
anchoh = (6/16)*(1/f0) # ancho del impulso rectangular
ht = lambda t: np.heaviside(t,1)-np.heaviside(t-anchoh,1)
# para DFT
N = 1*L # N par mayor que L, tramos DFT
# PROCEDIMIENTO
# muestreo de señal x[n]
t0 = 0 ; tn = 1/f0 # intervalo [t0,tn]
dt = (tn-t0)/L
ti = np.arange(t0,tn,dt)
xn = xt(ti)
hn = ht(ti)
# verificar que L<=N
if L<=N:
# DFT transformada rapida de Fourier
Xk = np.fft.fft(xn,n=N)
Xkmagn = np.abs(Xk) # para gráfica
Xkfase = np.angle(Xk)
k0x = np.argmax(Xk) # Pico |X[k]|
# DFT transformada rapida de Fourier
Hk = np.fft.fft(hn,n=N)
Hkmagn = np.abs(Hk) # para gráfica
Hkfase = np.angle(Hk)
k0h = np.argmax(Hk) # Pico |X[k]|
freq_Hz = np.fft.fftfreq(N,dt) # frecuencias en Hz
mitad = int(N/2)
# Convolucion en dominio de frecuencia
Yk = Hk*Xk
yn = np.fft.ifft(Yk,n=N)
yn_re = np.real(yn)
yn_im = np.imag(yn)
# SALIDA
if N>=L:
print('k0x:',k0x,'; i:',mitad+k0x)
print('freq_Hz:',freq_Hz[k0x],
'; Xk[k0x]:',Xk[k0x])
print('[ i, freq[ki],|X[k]| ,X[k]]')
kmin = k0x-4 ; kmax = k0x+4
if kmin<0:
kmin = 0
if kmax>N:
kmax = N
for i in range(kmin,kmax,1):
print([i,freq_Hz[i],Xkmagn[i],Xk[i]])
print()
print('k0h:',k0h,'; i:',mitad+k0h)
print('freq_Hz:',freq_Hz[k0h],
'; Hk[k0h]:',Hk[k0h])
print('[ i, freq[ki],|H[k]| ,H[k]]')
kmin = k0h-4 ; kmax = k0h+4
if kmin<0:
kmin = 0
if kmax>N:
kmax = N
for i in range(kmin,kmax,1):
print([i,freq_Hz[i],Hkmagn[i],Hk[i]])
else:
print('Revisar: L debe ser menor o igual a N')
print('L:',L,'; N:',N)
# GRAFICA
if N>=L:
LN_texto= ', L='+str(L)+', N='+str(N)
#zp_texto = 'zero padding:'+str(N-L)
plt.subplot(311)
plt.stem(np.real(xn),label='Re(x[n])',
markerfmt ='C2.',linefmt='C2-')
plt.stem(L,0,markerfmt ='C3.')
plt.xlabel('ti (s)')
plt.title('Convolución entre x[n],H[n]'+LN_texto)
plt.legend()
plt.subplot(312)
plt.stem(np.real(hn),label='Re(h[n])',
markerfmt ='C1.',linefmt='C1-')
plt.stem(L,0,markerfmt ='C1.')
plt.xlabel('ti (s)')
plt.legend()
plt.subplot(313)
plt.stem(np.real(yn),label='Re(y[n])',
markerfmt ='C0.',linefmt='C0-')
plt.stem(L,0,markerfmt ='C0.')
plt.xlabel('ti (s)')
plt.legend()
plt.tight_layout()
plt.show()