1. Interpolación Sinc(t)
Referencia: McClellan 4-3.6 p147
La interpolación con pulso Sinc(t) es un pulso relacionado con la Transformada de Fourier Contínua en tiempo. El pulso Sinc(t) es de ancho infinito y su amplitud disminuye al alejarse de cero, pero no llega a cero o la señal se mantiene en cero.
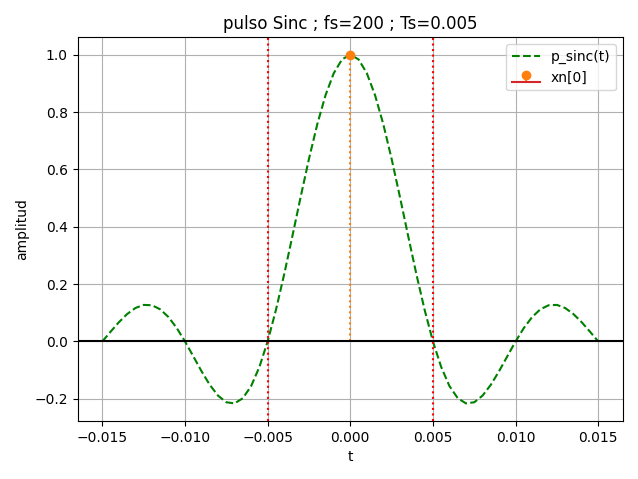
El valor de p(0)=1 y p(nTs) = 0 para n = ±1, ±2, ±3, ... El tipo de reconstrucción D-to-C es llamada interpolación de banda limitada, al ser equivalente a seleccionar los componentes de alias principal.
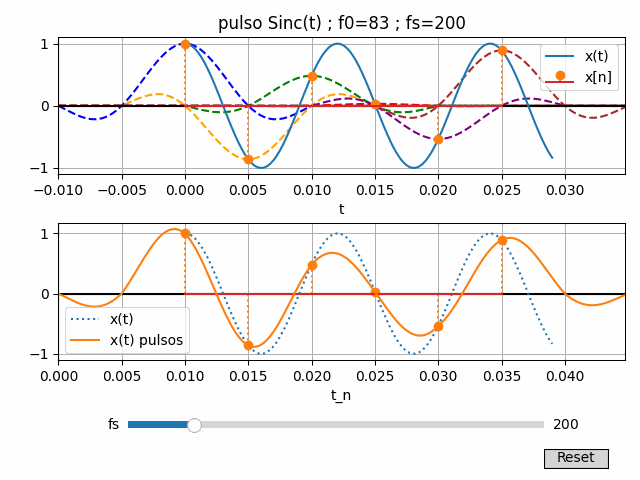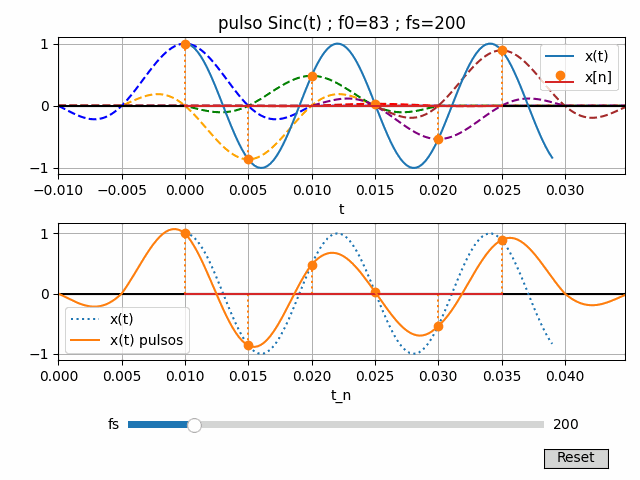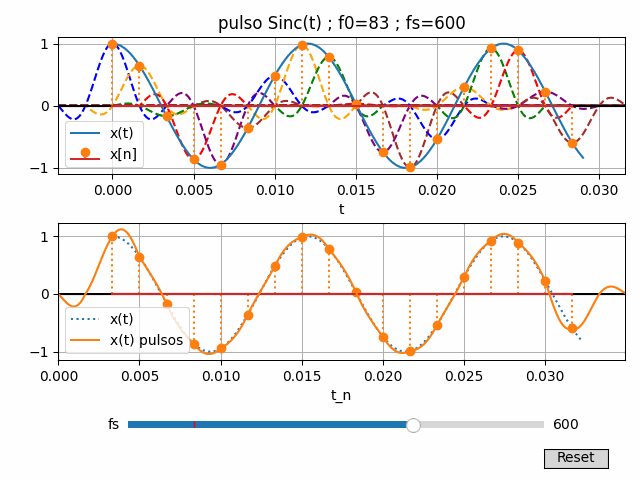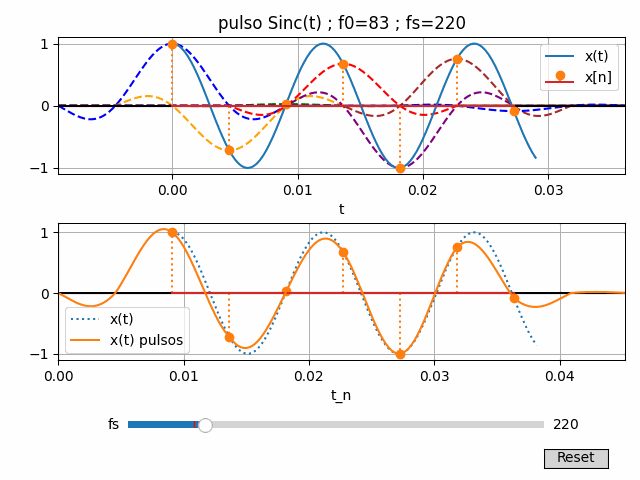
Si el muestreo cumple con las condiciones del teorema del muestreo, la reconstrucción de una onda cosenoidal es idéntica a la señal original que generó las muestras.
Una señal contínua x(t) de banda limitada sin componentes de frecuencia mayores a fmax se puede reconstruir exactamente a partir de las muestras x(n Ts), si las muestras se toman a una tasa de fs=1/Ts que es mayor que 2fmax.
2.1 Algoritmo en Python para un pulso Sinc(t)
El algoritmo es el mismo que para un pulso triangular, actualizando la sección de la función que define el pulso.
# D-to-C, Interpolacion con pulso Sinc(t)
# ejemplo 4.3.4 p144
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
fs = 200 # Hz muestreo
fs_veces = 10 # suavizar x(t), sobremuestreo
titulo = 'pulso Sinc'
nT = 3.0 # graficar periodos de la señal
# pulso Sinc
pulso_causal = True # No causal, pulso centrado en cero
pulso_ancho = 6
# PROCEDIMIENTO
Ts = 1/fs # muestreo periodo
dtc = Ts/fs_veces # suavizar x(t), sobremuestreo
#u = lambda t: np.piecewise(t,t>=0,[1,0])
u = lambda t: np.heaviside(t,1)
# pulso Sinc
u1 = lambda t: u(t+Ts*pulso_ancho/2)
u2 = lambda t: u(t-Ts*pulso_ancho/2)
sinc = lambda t: (np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t))
# x[n] interpolacion en Ts, a muestreo fs
t_unpulso = np.arange(-Ts*nT,Ts*nT+dtc,dtc)
unpulso = sinc(t_unpulso)
# SALIDA
print('muestras:',len(t_unpulso))
print('t_unpulso:',t_unpulso)
# GRAFICA de un pulso
plt.axhline(0,color='black')
plt.axvline(-Ts,color='red',linestyle='dotted')
plt.axvline(Ts,color='red',linestyle='dotted')
# p(t) componentes
plt.plot(t_unpulso,unpulso, color='green',linestyle='dashed',
label='p_sinc(t)')
plt.stem([0],[1],linefmt = 'C1:', label='xn[0]')
# grafica entorno
plt.xlabel('t')
plt.ylabel('amplitud')
texto = titulo + ' ; fs='+str(fs)
texto = texto +' ; Ts='+str(1/fs)
plt.title(texto)
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()
2. Ejercicio
Desarrollar el ejercicio de pulsos triangulares y su algoritmo para realizar la gráfica de la señal sin(2π(83)t) con interpolación de pulsos Sinc(t)
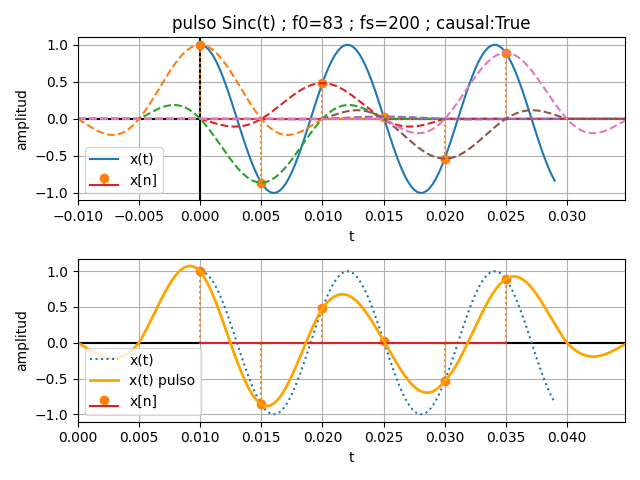
3. Algoritmo en Python Interpola con Sinc
# D-to-C, Interpolacion con pulso Sinc(t)
# ejemplo 4.3.4 p144
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
# señal x(t)
f0 = 83 # frecuencia de senal
fase0 = 0 # [0,2*np.pi]
xt = lambda t: np.cos(2*np.pi*f0*t + fase0)
fs = 200 # Hz muestreo
fs_veces = 20 # suavizar x(t), sobremuestreo
nT = 2.4 # graficar periodos de señal x(t)
titulo = 'pulso Sinc(t)'
# pulso Sinc
pulso_causal = True # No causal, centrado en cero
pulso_ancho = 4
casicero = 1e-10 # cero para valores menores
# PROCEDIMIENTO
Ts = 1/fs # tamaño de paso con fs
T = 1/f0 # periodo de señal
dtc = Ts/fs_veces # suavizar x(t), sobremuestreo
# muestreo x(t)
ti = np.arange(0,nT*T+dtc,dtc)
xti = xt(ti)
ti_max = max(ti)
# muestreo x[n]
muestras_n = 2
if ti_max>=Ts: # varias muestras
muestras_n = int(ti_max/Ts)+1
ki = np.arange(0,muestras_n,1,dtype=int)
tki = ki*Ts # muestras x[n]
xki = xt(tki)
tkj = tki # x[n] alias0
ti_0 = ti # No Causal, pulso centrado en cero
if pulso_causal: # Causal
tkj = tki + Ts*pulso_ancho/2
ti_0 = ti + Ts*pulso_ancho/2
xti_0 = xti
def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True):
''' tiempos para las n muestras x(t) con pulsos a frecuencia fs.
Para suavizar el pulso se usa fs_veces para el sobremuestreo.
El ancho del pulso es veces el periodo de muestreo (1/Ts)
Si es causal el tiempo inicia en t=0, centrado en cero.
Si no es causal el tiempo inicia t en mitad de intervalo.
'''
Ts = 1/fs # muestreo periodo
dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo
t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado
mitad = Ts*ancho/2
t_mitad = np.arange(0,mitad,dtc)
t_pulsos = np.copy(t_mitad) # mitad de primer pulso
for i in range(1,muestras_n,1):
t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc))
# mitad de último pulso para muestra_n
t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc))
if causal == False: # centrado en cero
t_pulsos = t_pulsos - mitad
return(t_pulsos)
# x[n] interpolacion en Ts, a muestreo fs
t_pulsos = pulso_ti(muestras_n,fs,fs_veces,
pulso_ancho,pulso_causal)
#u = lambda t: np.piecewise(t,t>=0,[1,0])
u = lambda t: np.heaviside(t,1)
# pulso Sinc(t) # tambien definido como np.sinc()
u1 = lambda t: u(t+Ts*pulso_ancho/2)
u2 = lambda t: u(t-Ts*pulso_ancho/2)
sinc_tl = lambda t: ((np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t)))
def sinc_t(t):
np.seterr(invalid='ignore') # t==0 division para cero
resultado = sinc_tl(t) # en t=0, resultado es nan
resultado = np.nan_to_num(resultado, nan=1) # cambia nan por 1
return (resultado)
# unpulso muestreo
t_unpulso = pulso_ti(1,fs,fs_veces,
pulso_ancho,pulso_causal)
t_pulsoEval= t_unpulso
if pulso_causal:
t_pulsoEval = t_unpulso-Ts*pulso_ancho/2
unpulso = sinc_t(t_pulsoEval)
muestras_pulso = len(t_unpulso)
muestras_N = len(xki)
mitad_pulso = int(muestras_pulso/2)
pulsos_vacio = np.zeros(len(t_pulsos),dtype=float)
xn_pulsos = np.copy(pulsos_vacio)
xk_pulsos = []
for j in range(0,muestras_N,1): # x[n] pulsos
k0 = int(j*fs_veces)
kn = k0 + muestras_pulso
pulsoj = np.copy(pulsos_vacio)
pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j]
xk_pulsos.append(pulsoj)
xn_pulsos = xn_pulsos+pulsoj
# SALIDA
print('muestras_pulso:',muestras_pulso)
print('t_unpulso:',t_unpulso)
print('muestras_tiempo:',len(t_pulsos))
# GRAFICAS ----------------------------
fig, [graf_t,graf_n] = plt.subplots(2,1)
# x(t) grafico entorno
t_causal = 0
if pulso_causal:
t_causal = Ts*pulso_ancho/2
graf_t.axhline(0,color='black')
graf_t.axvline(0,color='black')
graf_t.set_xlabel('t')
graf_t.set_ylabel('amplitud')
graf_t.set_xlim([t_pulsos[0]-t_causal,
t_pulsos[-1]-t_causal])
graf_t.grid()
texto = titulo + ' ; f0='+str(f0)
texto = texto + ' ; fs='+str(fs)
texto = texto + ' ; causal:'+str(pulso_causal)
graf_t.set_title(texto)
# x(t) componentes
graf_t.plot(ti,xti,label='x(t)')
graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:')
for i in range(0,muestras_N,1):
graf_t.plot(t_pulsos-t_causal,xk_pulsos[i],
linestyle='dashed')
graf_t.legend()
# x[n] grafico entorno
graf_n.axhline(0,color='black')
graf_n.axvline(0,color='black')
graf_n.set_xlabel('t')
graf_n.set_ylabel('amplitud')
graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]])
graf_n.grid()
# x[n] componentes
graf_n.plot(ti_0,xti_0,linestyle='dotted',
label='x(t)')
graf_n.stem(tkj,xki,label='x[n]',linefmt = 'C1:')
graf_n.plot(t_pulsos,xn_pulsos,
label='x(t) pulso',
lw=2, color='orange')
graf_n.legend()
plt.tight_layout()
plt.show()
4. Algoritmo en Python para gráfico interactivo con fs

# D-to-C, Interpolacion con pulso Sinc(t)
# grafico interactivo
# ejemplo 4.3.4 p144
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
# señal x(t)
f0 = 83 # frecuencia de senal
fase0 = 0 # [0,2*np.pi]
xt = lambda t: np.cos(2*np.pi*f0*t + fase0)
fs = 200 # Hz muestreo
fs_veces = 20 # suavizar x(t), sobremuestreo
nT = 2.4 # graficar periodos de señal x(t)
titulo = 'pulso Sinc(t)'
# pulso Sinc
pulso_causal = True # No causal, centrado en cero
pulso_ancho = 4
casicero = 1e-10 # cero para valores menores
# PROCEDIMIENTO
Ts = 1/fs # tamaño de paso con fs
T = 1/f0 # periodo de señal
dtc = Ts/fs_veces # suavizar x(t), sobremuestreo
def xt_actualiza(xt,f0,fs,fs_veces,nT,
pulso_ancho=1,pulso_causal=True):
''' x(t) muestreada a fs, para nT periodos de x(t).
gráfica suavizada con fs_veces. No causal, pulso centrado en cero.
Causal el pulso inicia en t=0.
'''
Ts = 1/fs # tamaño de paso con fs
T = 1/f0 # periodo de señal
dtc = Ts/fs_veces # suavizar x(t), sobremuestreo
# muestreo x(t)
ti = np.arange(0,nT*T+dtc,dtc)
xti = xt(ti)
ti_max = max(ti)
# muestreo x[n]
muestras_n = 2
if ti_max>=Ts: # varias muestras
muestras_n = int(ti_max/Ts)+1
ki = np.arange(0,muestras_n,1,dtype=int)
tki = ki*Ts # muestras x[n]
xki = xt(tki)
tkj = tki # x[n] alias0
ti_0 = ti # No Causal, pulso centrado en cero
if pulso_causal: # Causal
tkj = tki + Ts*pulso_ancho/2
ti_0 = ti + Ts*pulso_ancho/2
xti_0 = xti
return(ti,xti,tki,xki,tkj,ti_0,xti_0)
xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT,
pulso_ancho,pulso_causal)
[ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0
muestras_n = len(tki)
def pulso_ti(muestras_n,fs,fs_veces,ancho=1,causal=True):
''' tiempos para las n muestras x(t) con pulsos a frecuencia fs.
Para suavizar el pulso se usa fs_veces para el sobremuestreo.
El ancho del pulso es veces el periodo de muestreo (1/Ts)
Si es causal el tiempo inicia en t=0, centrado en cero.
Si no es causal el tiempo inicia t en mitad de intervalo.
'''
Ts = 1/fs # muestreo periodo
dtc = Ts/fs_veces # suavizar pulso(t), sobremuestreo
t_Ts = np.arange(0,Ts,dtc) # tiempo en periodo Ts sobremuestreado
mitad = Ts*ancho/2
t_mitad = np.arange(0,mitad,dtc)
t_pulsos = np.copy(t_mitad) # mitad de primer pulso
for i in range(1,muestras_n,1):
t_pulsos = np.concatenate((t_pulsos,t_Ts + t_pulsos[-1]+dtc))
# mitad de último pulso para muestra_n
t_pulsos = np.concatenate((t_pulsos,t_mitad + t_pulsos[-1]+dtc))
if causal == False: # centrado en cero
t_pulsos = t_pulsos - mitad
return(t_pulsos)
def xn_actualiza(fs,fs_veces,xki,
pulso_ancho=1,pulso_causal=True):
Ts = 1/fs # tamaño de paso con fs
T = 1/f0 # periodo de señal
dtc = Ts/fs_veces # suavizar x(t), sobremuestreo
#u = lambda t: np.piecewise(t,t>=0,[1,0])
u = lambda t: np.heaviside(t,1)
# pulso Sinc(t) # tambien definido como np.sinc()
u1 = lambda t: u(t+Ts*pulso_ancho/2)
u2 = lambda t: u(t-Ts*pulso_ancho/2)
sinc_tl = lambda t: ((np.sin(np.pi*t/Ts)/(np.pi*t/Ts))*(u1(t) - u2(t)))
def sinc_t(t):
np.seterr(invalid='ignore') # t==0 division para cero
resultado = sinc_tl(t) # en t=0, resultado es nan
resultado = np.nan_to_num(resultado, nan=1) # cambia nan por 1
return (resultado)
# x[n] interpolacion en Ts, a muestreo fs
muestras_n = len(xki)
t_pulsos = pulso_ti(muestras_n,fs,fs_veces,
pulso_ancho,pulso_causal)
# unpulso muestreo
t_unpulso = pulso_ti(1,fs,fs_veces,
pulso_ancho,pulso_causal)
t_pulsoEval= t_unpulso
if pulso_causal:
t_pulsoEval = t_unpulso-Ts*pulso_ancho/2
unpulso = sinc_t(t_pulsoEval)
muestras_pulso = len(t_unpulso)
muestras_N = len(xki)
mitad_pulso = int(muestras_pulso/2)
pulsos_vacio = np.zeros(len(t_pulsos),dtype=float)
xn_pulsos = np.copy(pulsos_vacio)
xk_pulsos = []
for j in range(0,muestras_N,1): # x(t) pulsos
k0 = int(j*fs_veces)
kn = k0 + muestras_pulso
pulsoj = np.copy(pulsos_vacio)
pulsoj[k0:kn]= pulsoj[k0:kn] + unpulso*xki[j]
xk_pulsos.append(pulsoj)
xn_pulsos = xn_pulsos+pulsoj
return(t_pulsos,xn_pulsos,t_unpulso,unpulso,xk_pulsos)
xn_list = xn_actualiza(fs,fs_veces,xki,
pulso_ancho,pulso_causal)
[t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n]
# SALIDA
# SALIDA
print('fs:',fs,'Hz ; Ts:',Ts,' s')
print('pulso_causal:',pulso_causal)
print('muestras_pulso:',len(t_unpulso))
print('t_unpulso:',t_unpulso)
print('muestras_tiempo:',len(t_pulsos))
# GRAFICAS interactivas----------------------------
from matplotlib.widgets import Slider, Button, TextBox
from matplotlib.collections import LineCollection
import telg1034 as dsp
colores = ["blue", "orange", "green", "red", "purple", "brown"]
fig, [graf_t,graf_n] = plt.subplots(2,1)
t_causal = 0
if pulso_causal:
t_causal = Ts*pulso_ancho/2
# lineas de cada pulso
muestras_n = len(tki)
tabla = []
for j in range(0,muestras_n,1):
pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0)
pulsoj = np.transpose(pulsoj)
tabla.append(pulsoj)
print('tamañotabla',np.shape(tabla))
linea_pulsosk = LineCollection(tabla,color=colores,
linestyles='dashed')
linea_pulsosk.set_array(t_pulsos)
graf_t.add_collection(linea_pulsosk)
# x(t) grafico entorno
graf_t.axhline(0,color='black')
graf_t.set_xlabel('t')
graf_t.grid()
texto = titulo + ' ; f0='+str(f0)
texto = texto +' ; fs='+str(fs)
graf_t.set_title(texto)
graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal])
# x(t) componentes
linea_xt, = graf_t.plot(ti,xti,label='x(t)')
puntos_xn = graf_t.stem(tki,xki,label='x[n]',linefmt = 'C1:')
#linea_pulso, = graf_t.plot(t_unpulso-t_causal,unpulso,
# label='pulso',linestyle='dashed',lw=2)
graf_t.legend()
# x[n] grafico entorno
graf_n.axhline(0,color='black')
graf_n.set_xlabel('t_n')
graf_n.grid()
# x[n] componentes
linea_xt0, = graf_n.plot(ti_0,xti_0,linestyle='dotted',
label='x(t)')
puntos_xki = graf_n.stem(tkj,xki,linefmt = 'C1:') #, label='x[n]')
linea_x_pulsos, = graf_n.plot(t_pulsos,x_pulsos,label='x(t) pulsos')
graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]])
graf_n.legend()
plt.tight_layout()
# plt.show()
# grafica interactiva
plt.subplots_adjust(bottom=0.25) # espacio widgets
# slider: barras para valores
# amplitud slider [x,y,ancho,alto]
fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03])
df_pasos = 5
fs_slider = Slider(fs_donde, 'fs',
(f0//df_pasos)*df_pasos,
(max([fs,10*f0])+2*df_pasos),
valinit = fs, valstep = df_pasos,
orientation='horizontal')
def grafico_actualiza(val):
# actualiza valores x,y
fs = fs_slider.val
Ts = 1/fs # tamaño de paso con fs
t_causal = 0
if pulso_causal:
t_causal = Ts*pulso_ancho/2
xt_list = xt_actualiza(xt,f0,fs,fs_veces,nT,
pulso_ancho,pulso_causal)
[ti,xti,tki,xki,tkj,ti_0,xti_0] = xt_list # x(t),x[n],x(t)_alias0
dsp.stem_update(puntos_xn,tki,xki,graf_t) # x[n]
dsp.stem_update(puntos_xki,tkj,xki,graf_n)
linea_xt0.set_xdata(ti_0) #x(t)_alias0
linea_xt0.set_ydata(xti_0)
xn_list = xn_actualiza(fs,fs_veces,xki,pulso_ancho,pulso_causal)
[t_pulsos,x_pulsos,t_unpulso,unpulso,xk_pulsos] = xn_list # x[n] pulsos, pulso
linea_x_pulsos.set_xdata(t_pulsos) # x[n] pulsos
linea_x_pulsos.set_ydata(x_pulsos)
#linea_pulso.set_xdata(t_unpulso-t_causal) # pulso lti
#linea_pulso.set_ydata(unpulso)
# lineas de cada pulso
muestras_n = len(tki)
tabla = []
for j in range(0,muestras_n,1):
pulsoj = np.concatenate(([t_pulsos-t_causal],[xk_pulsos[j]]),axis=0)
pulsoj = np.transpose(pulsoj)
tabla.append(pulsoj)
linea_pulsosk.set_segments(tabla)
texto = titulo+' ; f0='+str(f0)
texto = texto +' ; fs='+str(fs)
graf_t.set_title(texto)
graf_t.set_xlim([t_pulsos[0]-t_causal,t_pulsos[-1]-t_causal])
graf_n.set_xlim([t_pulsos[0],t_pulsos[-1]])
fig.canvas.draw_idle() # actualiza figura
# boton reinicio de gráfica
btn_rstdonde = plt.axes([0.85, 0.025, 0.1, 0.04])
btn_rst = Button(btn_rstdonde, 'Reset',
hovercolor='0.975')
def grafico_reinicia(event):
fs_slider.reset()
return()
# objetos interactivos
fs_slider.on_changed(grafico_actualiza)
btn_rst.on_clicked(grafico_reinicia)
plt.show()