1. Muestras de una señal
Referencia: McClellan 4.1 p123
Una señal discreta en tiempo x[n], representa como una secuencia ordenada de números que puede ser almacenada para su uso y procesamiento posterior. Las muestras de una señal contínua o analógica x(t) se encuentran espaciadas en el tiempo separadas por un tiempo Ts.
x[n] = x(nTs) =x(n/fs) ; -∞ <n < ∞
Cada valor de x[n] se denomina una muestra de la señal contínua x(t). Ts también se expresa como frecuencia de muestreo fs = 1/Ts en muestras/s.
1.1 Muestreo de una señal sinusoidal
Para obtener muestras de una señal x(t) = A cos(ωt+φ) se tiene que:
x[n] = x(nTs) = A cos(ωnTs +φ)
= A cos( (ωTs )n+φ)
= A cos(ωrad n+φ)
donde se tiene la frecuencia en radianes normalizada.
La frecuencia normalizada es un parámetro adimensional al quitar la unidad de tiempo de x(t), siendo 'n' el índice de posición en la secuencia de muestras.
2. Ejercicio
Referencia: McClellan Figura 4.3 p126
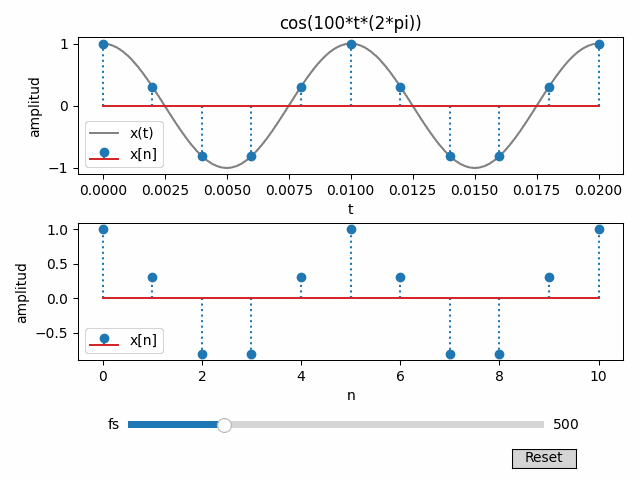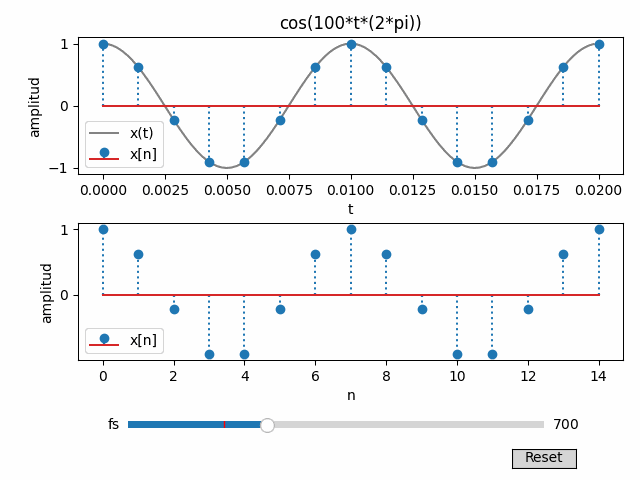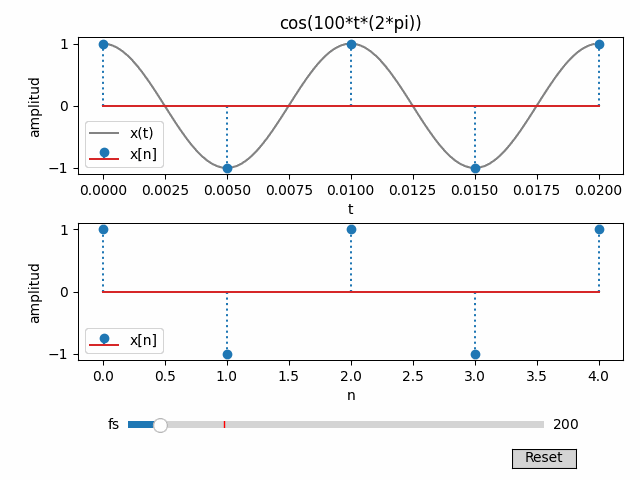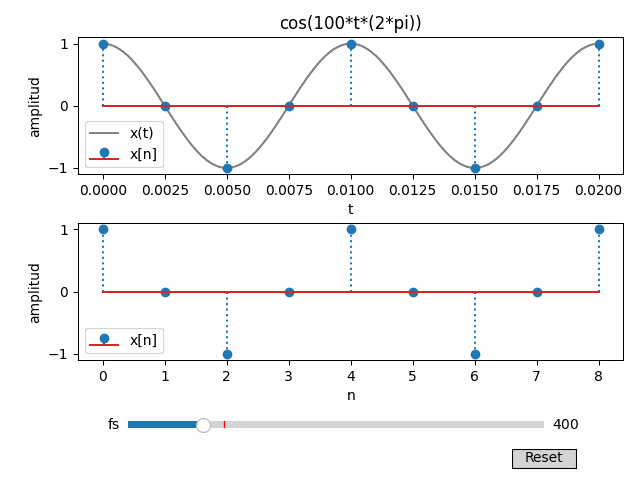
Una señal tipo coseno de 100 Hz se toman muestras con una tasa fs = 500 muestras/s. Realice y observe las gráficas de t y n correspondientes
x(t) = cos(2π(100)t)
muestreo: 11
tamaño ki: 11
tamaño ti: 100
fs: 500 ; dt: 0.002 ; fs_veces: 10
x(t): cos(100*t*(2*pi))
x[n]: cos(n*(2*pi)/5)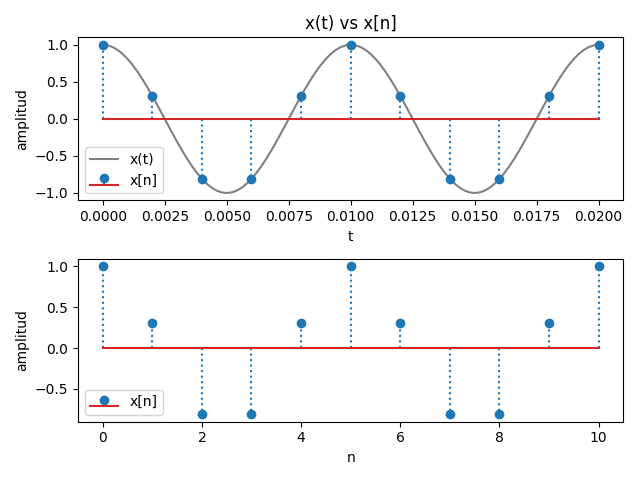
De la gráfica se puede observar que sin sobreponer la forma de onda x(t) sobre x[n] no es sencillo discernir la forma exacta de la forma de onda original. Para una mejor observación de x(t), se sobre-muestrea 10 veces la señal para que sea visiblemente semejante a la forma contínua.
3. Algoritmo en Python
# ejercicio figura 4.1 p126 Muestreo de señales sinusoidales
# telg1034 DSP fiec-espol edelros@espol.edu.ec
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
# variables continuas
t = sym.Symbol('t', real=True)
# variables discretas
n = sym.Symbol('n', integer=True, positive=True)
pi = sym.pi
DosPi = sym.UnevaluatedExpr(2*sym.pi)
equivalentes = [{'DiracDelta': lambda x: 1*(x==0)},
{'Heaviside': lambda x,y: np.heaviside(x, 1)},
'numpy',]
# INGRESO
# señal continua
f0 =100
x = sym.cos(f0*DosPi*t + 0)
# señal discreta
fs = 500 # muestreo discreto
Tn = 2 # periodos a graficar
fs_veces = 10 # suavizar x(t), sobremuestreo
# PROCEDIMIENTO
xt = sym.lambdify(t,x, modules=equivalentes)
xn = x.subs(t,n/fs)
# muestreo x[n]
muestras = int(Tn*(fs/f0))+1
if muestras<2:
muestras=2
ki = np.arange(0,muestras,1,dtype=int)
dt = 1/fs
tk = ki*dt
xk = xt(tk)
# muestreo x(t)
dtc = dt/fs_veces # sobremuestreo para x(t)
ti = np.arange(0,(muestras-1)*dt + dtc, dtc)
xti = xt(ti)
# SALIDA
print('muestreo:',muestras)
print(' tamaño ki:',len(ki))
print(' tamaño ti:',len(ti))
print('fs:',fs,' ; dt:',dt, ' ; fs_veces:',fs_veces)
print('x(t):',x)
print('x[n]:',xn)
# GRAFICA x(t) y x[n]
plt.subplot(211) # x(t) contínua
plt.plot(ti,xti, color='gray',label='x(t)')
plt.stem(tk,xk,linefmt = 'C0:',
label='x[n]')
plt.xlabel('t')
plt.ylabel('amplitud')
plt.title('x(t) vs x[n]')
plt.legend()
plt.subplot(212) # x[n] discreta
plt.stem(xk,linefmt = 'C0:',label='x[n]')
#plt.xticks(ki)
plt.xlabel('n')
plt.ylabel('amplitud')
plt.legend()
plt.tight_layout()
plt.show()
4. Muestreo - gráfico interactivo
Para el ejercicio de muestreo, se añade un control deslizante para la frecuencia de muestreo fs.
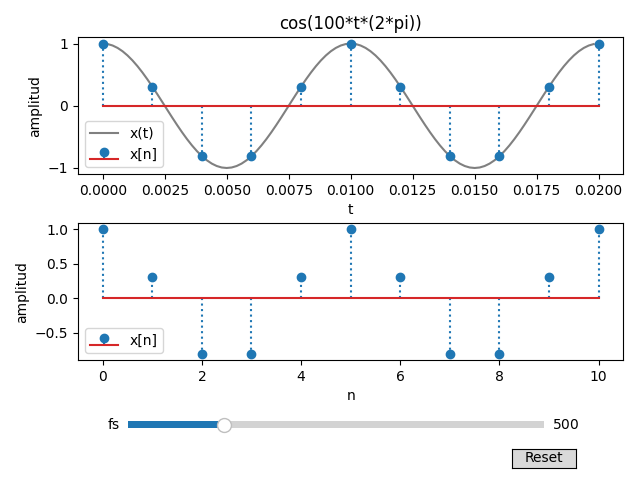
Se incorpora un botón de reinicio (Reset) para el valor predeterminado de fs.
El gráfico se actualiza o reinicia al interactuar con el control deslizante fs o el botón de reinicio.
# objetos interactivos
fs_slider.on_changed(grafico_actualiza)
btn_rst.on_clicked(grafico_reinicia)La actualización de gráfico se realiza solo para los puntos muestra en el eje tiempo y en el eje n.
Referencia: Gráficas 2D interactivas – matplotlib.widgets
4.1 Algoritmo en Python - muestreo interactivo para fs
Para el algoritmo se debe reemplazar la parte desde la gráfica # GRAFICA x(t) y x[n] , con las siguientes instrucciones que cambian a un objeto las lineas y los puntos para actualizar con cada interacción.
# GRAFICA x(t) y x[n] interactiva
from matplotlib.widgets import Slider, Button
fig, [grf1,grf2] = plt.subplots(2, 1)
# x(t) contínua
linea1, = grf1.plot(ti,xti, color='gray',label='x(t)')
puntos1 = grf1.stem(tk,xk,linefmt = 'C0:',
label='x[n]')
grf1.set_xlabel('t')
grf1.set_ylabel('amplitud')
grf1.set_title(x)
grf1.legend()
# x[n] discreta
puntos2 = grf2.stem(xk,linefmt = 'C0:',label='x[n]')
grf2.set_xlabel('n')
grf2.set_ylabel('amplitud')
grf2.legend()
plt.tight_layout()
# plt.show()
# grafica interactiva
plt.subplots_adjust(bottom=0.25) # espacio widgets
# slider: barras para valores
# amplitud slider [x,y,ancho,alto]
fs_donde = plt.axes([0.2, 0.10, 0.65, 0.03])
fs_slider = Slider(fs_donde, 'fs',
int(f0/2), f0*20,
valinit=fs,valstep= 10,
orientation='horizontal')
def stem_update(puntos,xdata,ydata,grafico):
'''actualiza puntos/tallos de plt.stem
con los datos de cada eje en un gráfico
'''
puntos.markerline.set_xdata(xdata)
puntos.markerline.set_ydata(ydata)
segmentos=[] # tallos o troncos
for j in range(0,len(xdata),1):
segmentos.append([[xdata[j],0],
[xdata[j],ydata[j]]])
puntos.stemlines.set_segments(segmentos)
puntos.baseline.set_xdata([xdata[0],xdata[-1]])
grafico.relim()
grafico.autoscale_view()
return(puntos,grafico)
def grafico_actualiza(val):
# actualiza valores x,y
fs = fs_slider.val
muestras = int(Tn*(fs/f0))+1
if muestras<2:
muestras=2
ki = np.arange(0,muestras,1,dtype=int)
dt = 1/fs
tk = ki*dt
xk = xt(tk)
print('f0:',f0,' ;fs:',fs,' ',tipomuestreo)
# actualiza grafico
stem_update(puntos1,tk,xk,grf1)
stem_update(puntos2,ki,xk,grf2)
fig.canvas.draw_idle() # actualiza figura
# boton reinicio de gráfica
btn_rstdonde = plt.axes([0.8, 0.025, 0.1, 0.04])
btn_rst = Button(btn_rstdonde, 'Reset',
hovercolor='0.975')
def grafico_reinicia(event):
fs_slider.reset()
return()
# objetos interactivos
fs_slider.on_changed(grafico_actualiza)
btn_rst.on_clicked(grafico_reinicia)
plt.show()