1. Ejercicio: Circuito RLC
Referencia: Lathi 1.8-1 p111. Oppenheim problema 2.61c p164, Ejemplo 9.24 p700
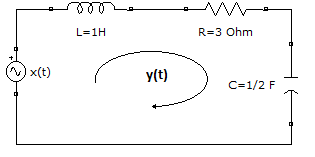
Siguiendo con el ejemplo de la referencia planteado en "Sistema LTIC – Modelo entrada-salida" y las instrucciones del desarrollo analítico para "LTIC - Respuesta entrada cero", se tiene la expresión:
\frac{d^2}{dt^2}y(t) +3\frac{d}{dt}y(t) + 2y(t) = \frac{d}{dt}x(t)Se prefiere escribir el termino de mayor orden primero y para entrada cero.Se tiene que x(t)=0, con condiciones iniciales y(0)=0, y'(0)=-5.
(D^2 + 3D +2)y(t) = 02. ZIR Respuesta entrada cero - desarrollo numérico con Scipy-Python
Esta forma de describir el problema simplifica el desarrollo a partir de la descripción de la ecuación del sistema.
Scipy define un sistema LTI usando los coeficientes de la ecuación ordenados como la expresión P(D)/Q(D con la función Scipy.signal.lti().
Se describe una señal de entrada x(t), muestreada en un intervalo [a,b] junto a las condiciones iniciales en un vector [y'(0),y(0)].
El resultado será la simulación del paso de la señal x(t) por el sistema LTI, usando la función scipy.signal.lsim(), con lo que se obtiene la respuesta del sistema y(t) y los componentes yc=[yi(t),y0(t)], donde y0(t) representa la respuesta a entrada cero.
El algoritmo tiene el siguiente resultado:

Algoritmo en Python con Scipy
# Sistema lineal usando scipy.signal
# Q(D)y(t)=P(D)x(t)
# ejemplo: (D^2+3D+2)y(t)=(D+0)x(t)
import numpy as np
import scipy.signal as senal
import matplotlib.pyplot as plt
# INGRESO
# tiempo [a,b] intervalo observación
a = 0 ; b = 5 # intervalo tiempo [a,b]
muestras = 41
# Señal de entrada x(t) = 0
x = lambda t: t*0
# Sistema LTI
# coeficientes Q P de la ecuación diferencial
Q = [1., 3., 2.]
P = [1., 0.]
# condiciones iniciales [y'(0),y(0)]
cond_inicio = [-5,0]
# PROCEDIMIENTO
# intervalo observado
ti = np.linspace(a, b, muestras)
xi = x(ti)
sistema = senal.lti(P,Q)
# respuesta entrada cero
[t_y, yi, yc] = senal.lsim(sistema, xi, ti, cond_inicio)
# respuesta a impulso
[t_h, hi] = sistema.impulse(T = ti)
# SALIDA - GRAFICA
plt.subplot(211)
plt.suptitle('Respuesta a Entrada cero')
plt.plot(ti, xi, color='blue', label='x(t)')
#plt.plot(t_h, hi, color='red', label='h(t)')
plt.legend()
plt.grid()
plt.subplot(212)
# plt.plot(t_y, yi, color='magenta', label='y(t)')
# plt.plot(t_y, yc[:,0], 'g-.', label='y(t)')
plt.plot(t_y, yc[:,1], color='orange', label='y0(t)')
plt.xlabel('t')
plt.legend()
plt.grid()
plt.show()
3. ZIR Respuesta entrada cero - desarrollo numérico con Runge-Kutta de Métodos numéricos en Python
Se reordena el sistema de ecuaciones para plantear una solución con el algoritmo Runge-Kutta de 2do orden para ecuaciones diferenciales con segundas derivadas
(D^2 + 3D +2)y(t) = 0 D^2 y(t) + 3Dy(t) + 2y(t) = 0Se ubica el término de mayor grado a la izquierda de la ecuación:
D^2 y(t) = - 3Dy(t) - 2y(t)sustituyendo las expresiones de las derivadas como las funciones f(x) por z y g(x) por z':
Dy = y' = z = f(x)
D2y = y" = z'= -3z - 2y = g(x)
Los valores iniciales de t0=0, y0=0, z0=-5 se usan en el algoritmo.
En este caso también se requiere conocer un intervalo de tiempo a observar [0,tn=5] y definir el tamaño de paso o resolución del resultado h=dt=0.1
El algoritmo permite obtener la gráfica y la tabla de datos.

Algoritmo en Python con Runge-Kutta
# Respuesta a entrada cero
# solucion para (D^2+ D + 1)y = 0
import numpy as np
import matplotlib.pyplot as plt
def rungekutta2_fg(f,g,x0,y0,z0,h,muestras):
tamano = muestras + 1
estimado = np.zeros(shape=(tamano,3),dtype=float)
# incluye el punto [x0,y0]
estimado[0] = [x0,y0,z0]
xi = x0
yi = y0
zi = z0
for i in range(1,tamano,1):
K1y = h * f(xi,yi,zi)
K1z = h * g(xi,yi,zi)
K2y = h * f(xi+h, yi + K1y, zi + K1z)
K2z = h * g(xi+h, yi + K1y, zi + K1z)
yi = yi + (K1y+K2y)/2
zi = zi + (K1z+K2z)/2
xi = xi + h
estimado[i] = [xi,yi,zi]
return(estimado)
# PROGRAMA
f = lambda t,y,z: z
g = lambda t,y,z: -3*z -2*y
t0 = 0
y0 = 0
z0 = -5
h = 0.1
tn = 5
muestras = int((tn-t0)/h)
tabla = rungekutta2_fg(f,g,t0,y0,z0,h,muestras)
ti = tabla[:,0]
yi = tabla[:,1]
zi = tabla[:,2]
# SALIDA
np.set_printoptions(precision=6)
print('ti, yi, zi')
print(tabla)
# GRAFICA
plt.plot(ti,yi, color = 'orange', label='y0(t)')
plt.ylabel('y(t)')
plt.xlabel('t')
plt.title('Entrada cero con Runge-Kutta 2do Orden d2y/dx2 ')
plt.legend()
plt.grid()
plt.show()
Más detalles del algoritmo de Runge-Kutta para segunda derivada en 6.3 EDO d2y/dx2, Runge-Kutta con Python
4. LTI CT - Respuesta a entrada cero - Diagrama Bloques con XCOS-Scilab

Para XCOS, se añade un visor de señal de salida (Sinks/Scope) y un reloj de muestreo. Para y'(0)=5 siguiendo el diagrama se ubica y'(t)=dy/dt como la salida del primer integrador . El valor se cambia dando doble click al elemento marcado en rojo y escribiendo el valor de -5.

La gráfica se obtiene usando el osciloscopio (scope)

El tiempo de observación se establece con el valor de "Simulatión/Final Integration time" a 5 segundos.

De forma semejante se puede realizar el ejercicio en otros simuladores, como por ejemplo Simulink-Matlab.
4.1 Desarrollo como circuito en simulador
La simulación en forma de circuito usando las herramientas de Simulink/Matlab y SimPowerSystems, para cada componente (Elements) se crea con "Series RLC Branch".
Para extraer las lecturas de las señal se usa un medidor (Measurements) que se ubica en serie con los demás componentes y se visualiza con un osciloscopio (Simulink/Commonly Used Blocks/Scope).
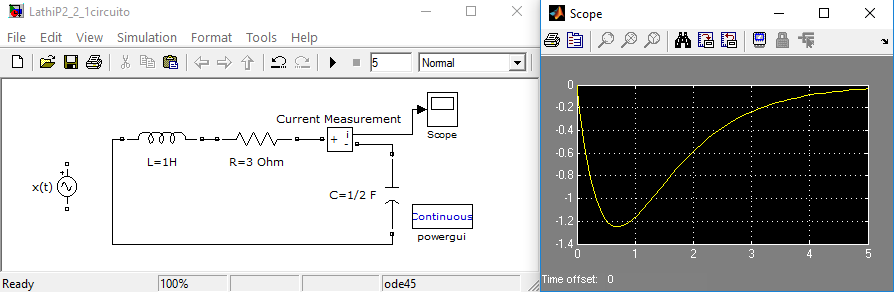
Las conexiones son similares a las que se usarían en el laboratorio. Se puede observar que las respuestas serán las mismas.
Las condiciones iniciales se pueden establecer en los componentes que pueden tener un valor inicial como el capacitor en 5 voltios.
El signo de la corriente de salida ya está incluido en la inversión de polaridad respecto a la polaridad de la fuente.