Ejemplos para interpretar de series de Fourier de señales periódicas contínuas a partir del algoritmo de la sección anterior.
1. Señal exponencial periódica con n términos de Fourier
Referencia: Lathi Ej 6.1 p599
Encuentre serie de Fourier para la señal x(t) y muestre el espectro de amplitud y fase de x(t)
x(t) = e^{-\frac{t}{2}} \text{ , }{0 \leq t \leq \pi}
siendo el periodo T0 = π y la frecuencia fundamental f0 = 1/T0 = 1/π Hz,
\omega_0 = \frac{a \pi}{T_0} = 2 \text{ rad/s}1.1 Desarrollo analítico
x(t) = a_0 +\sum_{n=1}^{\infty} a_n \cos (2 n t) +b_n \sin (2 n t) a_0 = \frac{1}{\pi} \int_{0}^{\pi} e^{-t/2} \delta t = 0.504 a_n = \frac{2}{\pi} \int_{0}^{\pi} e^{-t/2} \cos(2 n t) \delta t = 0.504 \Big( \frac{2}{1+16 n^2}\Big) b_n = \frac{2}{\pi} \int_{0}^{\pi} e^{-t/2} \sin (2 n t) \delta t = 0.504\Big( \frac{8n}{1+16 n^2}\Big) x(t) = 0.504\Big[ 1 +\sum_{n=1}^{\infty} \Big( \frac{2}{1+16 n^2} \Big)(\cos (2 n t) + 4n \sin (2 n t))\Big]Serie de Fourier en la forma exponencial,
C_0 = a_0 = 0.504 C_n = \sqrt{a_n^2 + b_n^2} = 0.504\sqrt{ \Big(\frac{2}{1+16 n^2}\Big) ^2 + \Big( \frac{8n}{1+16 n^2} \Big) ^2 } C_n = 0.504\Big( \frac{8}{\sqrt{1+16 n^2}} \Big) \theta_n = \tan ^{-1} \Big( \frac{-b_n}{a_n}\Big) = \tan^{-1} (-4n) = -\tan^{-1}(4n)con lo que se puede expresar x(t) como,
serie de Fourier fs(t), n términos no cero:
+ 0.504279523791290
+ 0.0593270027989753*cos(2*t)
+ 0.015516293039732*cos(4*t)
+ 0.00695557963850055*cos(6*t)
+ 0.00392435427074934*cos(8*t)
+ 0.00251510984434559*cos(10*t)
+ 0.00174793595768211*cos(12*t)
+ 0.0012847885956466*cos(14*t)
+ 0.00098396004642203*cos(16*t)
+ 0.000777609134604919*cos(18*t)
+ 0.000629955682437589*cos(20*t)
+ 0.237308011195901*sin(2*t)
+ 0.124130344317856*sin(4*t)
+ 0.0834669556620066*sin(6*t)
+ 0.0627896683319894*sin(8*t)
+ 0.0503021968869117*sin(10*t)
+ 0.0419504629843708*sin(12*t)
+ 0.0359740806781048*sin(14*t)
+ 0.0314867214855049*sin(16*t)
+ 0.0279939288457771*sin(18*t)
+ 0.0251982272975036*sin(20*t)
coeficientes:
['k_i', 'ak', 'bk', 'ck', 'cfs']
0 ak: 0.50427952379129 bk: 0
ck: 0.50427952379129 cfs: 0
1 ak: 0.0593270027989753 bk: 0.2373080111959012
ck: 0.24461149899148976 cfs: -1.3258176636680326
2 ak: 0.015516293039732001 bk: 0.12413034431785602
ck: 0.1250963537844502 cfs: -1.4464413322481353
3 ak: 0.006955579638500553 bk: 0.08346695566200663
ck: 0.08375627006732632 cfs: -1.4876550949064553
4 ak: 0.003924354270749339 bk: 0.06278966833198943
ck: 0.06291218487450254 cfs: -1.5083775167989393
5 ak: 0.0025151098443455863 bk: 0.05030219688691173
ck: 0.05036503538347567 cfs: -1.5208379310729538
6 ak: 0.0017479359576821145 bk: 0.04195046298437075
ck: 0.04198686252526162 cfs: -1.5291537476963082
7 ak: 0.001284788595646599 bk: 0.03597408067810477
ck: 0.035997016020363336 cfs: -1.5350972141155728
8 ak: 0.0009839600464220293 bk: 0.031486721485504944
ck: 0.031502092109552245 cfs: -1.5395564933646284
9 ak: 0.0007776091346049191 bk: 0.02799392884577709
ck: 0.02800472689009217 cfs: -1.5430256902014756
10 ak: 0.000629955682437589 bk: 0.025198227297503564
ck: 0.025206100513536184 cfs: -1.5458015331759765
>>>1.2 Algoritmo en Python
# Serie de Fourier, espectro con n coeficientes
# Lathi ej 6.1 p599
import numpy as np
import sympy as sym
# INGRESO
t = sym.Symbol('t', real=True,)
T0 = sym.pi ; t0 = 0 # periodo ; t_inicio
ft = sym.exp(-t/2)
n = 11 # número de coeficientes
t_a = t0 # intervalo de t =[t_a,t_b]
t_b = t0 + T0
# PROCEDIMIENTO
serieF = sym.fourier_series(ft,(t,t0,t0+T0))
serieFk = serieF.truncate(n)
def fourier_series_coef(serieF,n,T0, casicero=1e-10):
''' coeficientes de serie de Fourier
ak,bk,ck_mag, ck_fase
'''
w0 = 2*sym.pi/T0
ak = [float(serieF.a0.evalf())]
bk = [0]; k_i=[0]
ak_coef = serieF.an
bk_coef = serieF.bn
ck_mag = [ak[0]] ; ck_fase = [0]
for i in range(1,n,1):
ak_valor = ak_coef.coeff(i).subs(t,0)
ak_valor = float(ak_valor.evalf())
ak.append(ak_valor)
bk_term = bk_coef.coeff(i).evalf()
bk_valor = 0
term_mul = sym.Mul.make_args(bk_term)
for term_k in term_mul:
if not(term_k.has(sym.sin)):
bk_valor = float(term_k)
else: # sin(2*w0*t)
ki = term_k.args[0].subs(t,1)/w0
bk.append(bk_valor)
k_i.append(i)
# magnitud y fase
ak_signo = 1 ; bk_signo = 1
if abs(ak_valor)>casicero:
ak_signo = np.sign(ak_valor)
if abs(bk_valor)>casicero:
bk_signo = np.sign(bk_valor)
signo_ck = ak_signo*bk_signo
ck_mvalor = signo_ck*np.sqrt(ak_valor**2 + bk_valor**2)
ck_mag.append(ck_mvalor)
pendiente = np.nan
if (abs(ak_valor)>=casicero):
pendiente = -bk_valor/ak_valor
ck_fvalor = np.arctan(pendiente)
ck_fase.append(ck_fvalor)
coef_fourier = {'k_i': k_i,'ak': ak,'bk': bk,
'ck_mag' : ck_mag,'ck_fase': ck_fase}
return (coef_fourier)
coef_fourier = fourier_series_coef(serieF,n,T0)
# SALIDA
#print('\n serie de Fourier fs(t): ')
#sym.pprint(serieF)
print('\n serie de Fourier fs(t), n términos no cero: ')
term_suma = sym.Add.make_args(serieFk)
for term_k in term_suma:
operador = '+'
factor_mul = sym.Mul.make_args(term_k)
for factor_k in factor_mul:
if not(factor_k.has(t)):
if sym.sign(factor_k)<0:
operador = ''
print(operador,term_k.evalf())
print('\n coeficientes: ')
m = len(coef_fourier['k_i'])
print(list(coef_fourier.keys()))
for i in range(0,m,1):
print(str(coef_fourier['k_i'][i]),
'ak:',str(coef_fourier['ak'][i]),
'bk:',str(coef_fourier['bk'][i]) )
print(' ','ck_mag:',str(coef_fourier['ck_mag'][i]),
'ck_fase:',str(coef_fourier['ck_fase'][i]) )
gráfica de la serie de Fourier comparada con f(t) en un periodo,

Espectro de frecuencias,

1.3 Gráficas en Python
Complementarias para realizar las gráficas, en un periodo, en varios periodos con periodo central destacado y espectro de frecuencias
# GRAFICA ----------------
import matplotlib.pyplot as plt
import telg1001 as ss
equivalentes = [{'DiracDelta': lambda x: 1*(x==0)},
{'Heaviside': lambda x,y: np.heaviside(x, 1)},
'numpy',]
# Evaluación para gráfica
muestras = 101
t_a = float(t_a) ; t_b = float(t_b)
figura_ft = ss.graficar_ft(ft,t_a,t_b,muestras)
ti = np.linspace(t_a,t_b,muestras)
# convierte a sympy una constante
serieF_k = sym.sympify(serieFk,t)
if serieFk.has(t): # no es constante
serieF_t = sym.lambdify(t,serieF_k,modules=equivalentes)
else:
serieF_t = lambda t: serieF_k + 0*t
SerieFi = serieF_t(ti) # evalua ti
etiqueta = 'coeficientes = '+ str(n)
figura_ft.axes[0].plot(ti,SerieFi,'orange',
label = etiqueta)
figura_ft.axes[0].legend()
ft_etq = ''
if not(ft.has(sym.Piecewise)):
ft_etq = '$ = '+str(sym.latex(ft)) +'$'
etiq_1 = 'f(t) '+ft_etq+' ; $T_0='+str(sym.latex(T0))+'$'
figura_ft.axes[0].set_title(r'Serie de Fourier '+etiq_1)
#plt.show()
def graficar_ft_periodoT0(ft,t0,T0,muestras=51,
n_periodos=4,f_nombre='f'):
''' grafica f(t) en intervalo[t0,t0+T0] para n_periodos
'''
# convierte a sympy una constante
ft = sym.sympify(ft,t)
if ft.has(t): # no es constante
f_t = sym.lambdify(t,ft,modules=equivalentes)
else:
f_t = lambda t: ft + 0*t
# intervalo de n_periodos
ti = np.linspace(float(t0-T0*n_periodos/2),
float(t0+T0*n_periodos/2),
n_periodos*muestras)
fk = np.zeros(n_periodos*muestras)
# ajuste de intervalo por periodos
ti_T0 = (ti-t0)%float(T0)+t0
fi = f_t(ti_T0)
# intervalo de UN periodo
ti0 = np.linspace(float(t0),float(t0+T0),muestras)
fi0 = f_t(ti0)
fig_fT0, graf_fT0 = plt.subplots()
graf_fT0.plot(ti,fi,label=f_nombre+'(t)',
color= 'blue',linestyle='dashed')
graf_fT0.plot(ti0,fi0,label=f_nombre+'(t)',color= 'blue')
graf_fT0.axvline(t0, color ='red')
graf_fT0.axvline(t0+T0, color ='red')
graf_fT0.set_xlabel('t')
graf_fT0.set_ylabel(f_nombre+'(t)')
graf_fT0.legend()
graf_fT0.grid()
ft_etq = '' ; ft_ltx =''
if not(ft.has(sym.Piecewise)):
ft_etq = '$ = '+str(sym.latex(ft)) +'$'
etiq_1 = r''+f_nombre+'(t) '+ft_etq+' ; $T_0='+str(sym.latex(T0))+'$'
graf_fT0.set_title(etiq_1)
return(fig_fT0)
def graficar_w_espectro(coef_fourier,T0,f_nombre='f'):
''' coef_fourier es diccionario con entradas
['k_i','ck_mag','ck_fase'] indice, Ck_magnitud, Ck_fase
'''
# espectro de frecuencia
k_i = coef_fourier['k_i']
ck = coef_fourier['ck_mag']
cfs = coef_fourier['ck_fase']
# grafica de espectro de frecuencia
fig_espectro_w, graf_spctr = plt.subplots(2,1)
graf_spctr[0].stem(k_i,ck,label='Ck_magnitud')
graf_spctr[0].set_ylabel('|Ck|')
graf_spctr[0].legend()
graf_spctr[0].grid()
ft_etq = '' ; ft_ltx =''
if not(ft.has(sym.Piecewise)):
ft_etq = '$ = '+str(sym.latex(ft)) +'$'
etiq_2 = ft_etq+' ; $T_0='+str(sym.latex(T0))+'$'
etiq_1 = r'Espectro frecuencia '+f_nombre+'(t) '
graf_spctr[0].set_title(etiq_1+etiq_2)
graf_spctr[1].stem(k_i,cfs,label='Ck_fase')
graf_spctr[1].legend()
graf_spctr[1].set_ylabel('Ck_fase')
graf_spctr[1].set_xlabel('k')
graf_spctr[1].grid()
return(fig_espectro_w)
fig_fT0 = graficar_ft_periodoT0(ft,t0,T0,muestras,f_nombre='x')
fig_espectro_w = graficar_w_espectro(coef_fourier,T0,f_nombre='x')
plt.show()
2. Ejemplo. Señal triangular periódica
Referencia: Lathi Ej 6.2 p602
Encuentre serie de Fourier para la señal x(t) y muestre el espectro de amplitud y fase de x(t)
x(t) = \begin{cases} 4t & t < -\frac{1}{4} \\ -4t+4 & t \leq \frac{3}{4} \end{cases}
en el algoritmo el bloque de ingreso se escribe el periodo, intervalo y la función como:
T0 = 2 ; t0 = -T0/4 # periodo ; t_inicio
A = 2
ft = sym.Piecewise((0, t<(-T0/4)),
((4*A/T0)*t, t<(T0/4)),
(-(4*A/T0)*t+2*A, t<=(3*T0/4)),
(0, True))
n = 9 # número de coeficientesSerie de Fourier en forma trigonométrica:
serie de Fourier fs(t), n términos no cero:
+ 1.6211389382774*sin(pi*t)
+ 0.0200140609663877*sin(9*pi*t)
+ 0.00560947729507752*sin(17*pi*t)
+ 0.0648455575310962*sin(5*pi*t)
+ 0.009592538096316*sin(13*pi*t)
-0.0133978424651025*sin(11*pi*t)
-0.180126548697489*sin(3*pi*t)
-0.00720506194789958*sin(15*pi*t)
-0.0330844681281103*sin(7*pi*t)
coeficientes:
['k_i', 'ak', 'bk', 'ck', 'cfs']
0 ak: 0.0 bk: 0
ck: 0.0 cfs: 0
1 ak: 0.0 bk: 1.6211389382774044
ck: 1.6211389382774044 cfs: nan
2 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
3 ak: 0.0 bk: -0.18012654869748937
ck: 0.18012654869748937 cfs: nan
4 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
5 ak: 0.0 bk: 0.06484555753109618
ck: 0.06484555753109618 cfs: nan
6 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
7 ak: 0.0 bk: -0.03308446812811029
ck: 0.03308446812811029 cfs: nan
8 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nanComparando la serie de Fourier con f(t)

Espectro de frecuencias de f(t)

3. Ejemplo. Señal rectangular periódica
Referencia: Lathi Ej 6.4 p605, Oppenheim Ej 4.5 p294
Encuentre serie de Fourier para la señal x(t) y muestre el espectro de amplitud y fase de x(t)
x(t) = \begin{cases} 0 & t \frac{\pi}{2}\end{cases}T0 = 2*sym.pi ; t0 = -T0/2 # periodo ; t_inicio
ft = sym.Piecewise((0, t<-(T0/4)),
(1, t<(T0/4)),
(0, t<(T0/2)),
(0, True))
n = 9 # numero de coeficientesla gráfica de f(t) dentro de un periodo:
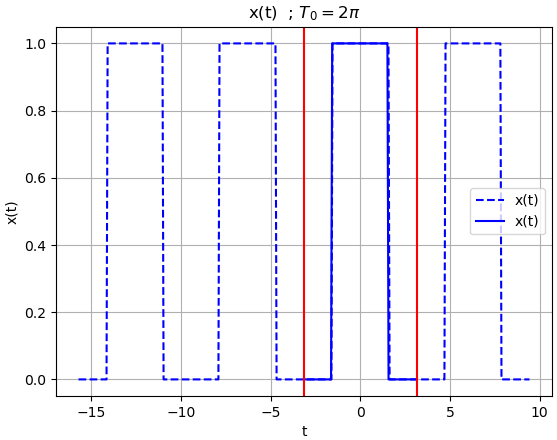
la serie de Fourier en forma trigonométrica
serie de Fourier fs(t), n términos no cero:
+ 0.500000000000000
+ 0.636619772367581*cos(0.318309886183791*pi*t)
+ 0.0489707517205832*cos(4.13802852038928*pi*t)
+ 0.0707355302630646*cos(2.86478897565412*pi*t)
+ 0.127323954473516*cos(1.59154943091895*pi*t)
-0.0909456817667973*cos(2.22816920328654*pi*t)
-0.0578745247606892*cos(3.5014087480217*pi*t)
-0.0424413181578388*cos(4.77464829275686*pi*t)
-0.212206590789194*cos(0.954929658551372*pi*t)
coeficientes:
['k_i', 'ak', 'bk', 'ck', 'cfs']
0 ak: 0.5 bk: 0
ck: 0.5 cfs: 0
1 ak: 0.6366197723675814 bk: 0.0
ck: 0.6366197723675814 cfs: -0.0
2 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
3 ak: -0.21220659078919377 bk: 0.0
ck: -0.21220659078919377 cfs: 0.0
4 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
5 ak: 0.12732395447351627 bk: 0.0
ck: 0.12732395447351627 cfs: -0.0
6 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
7 ak: -0.09094568176679733 bk: 0.0
ck: -0.09094568176679733 cfs: 0.0
8 ak: 0.0 bk: 0.0
ck: 0.0 cfs: nan
>>>
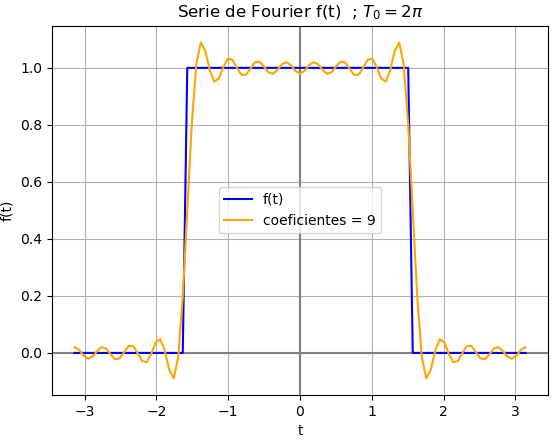
comparando la serie de Fourier con f(t):
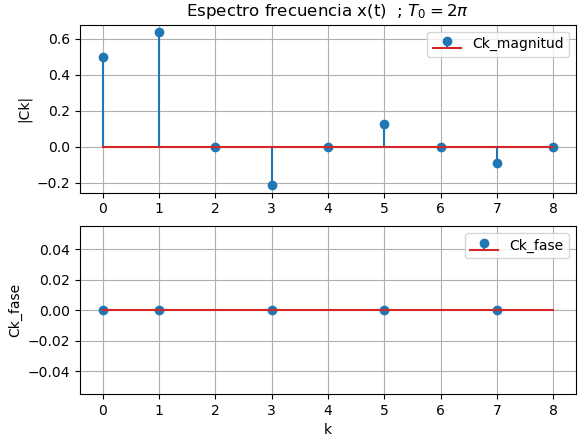
el espectro de frecuencias,