Autor: Edison Del Rosario

8.3.1 Regresión polinomial de grado m - Ejercicio Temperatura para un día con Python

De una estación meteorológica se obtiene un archivo.csv con los datos de los sensores disponibles durante una semana.

2021OctubreEstMetorologica.csv

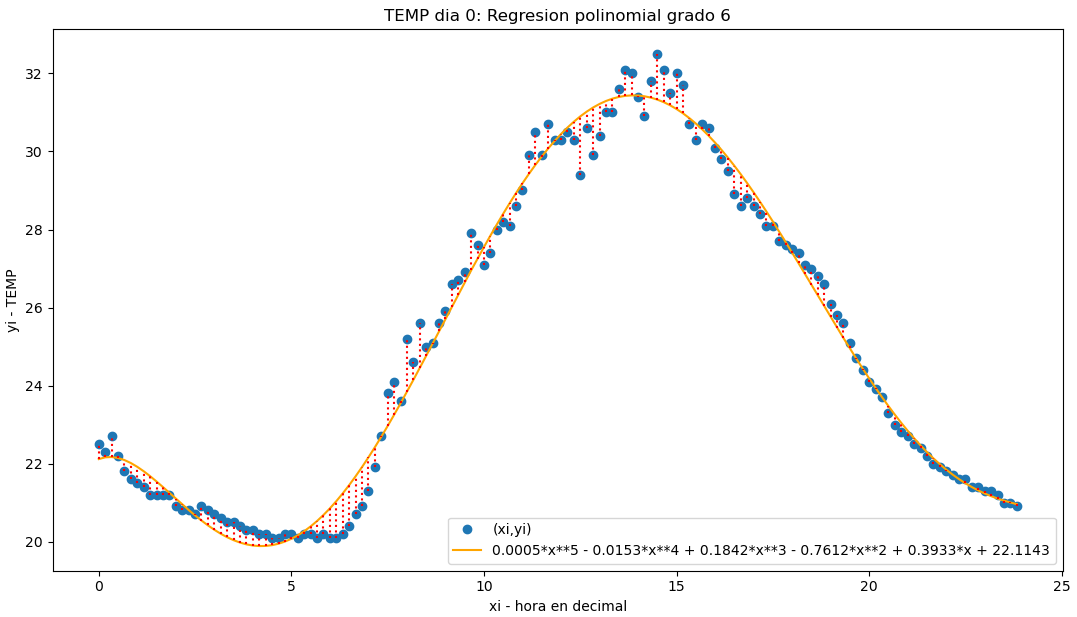
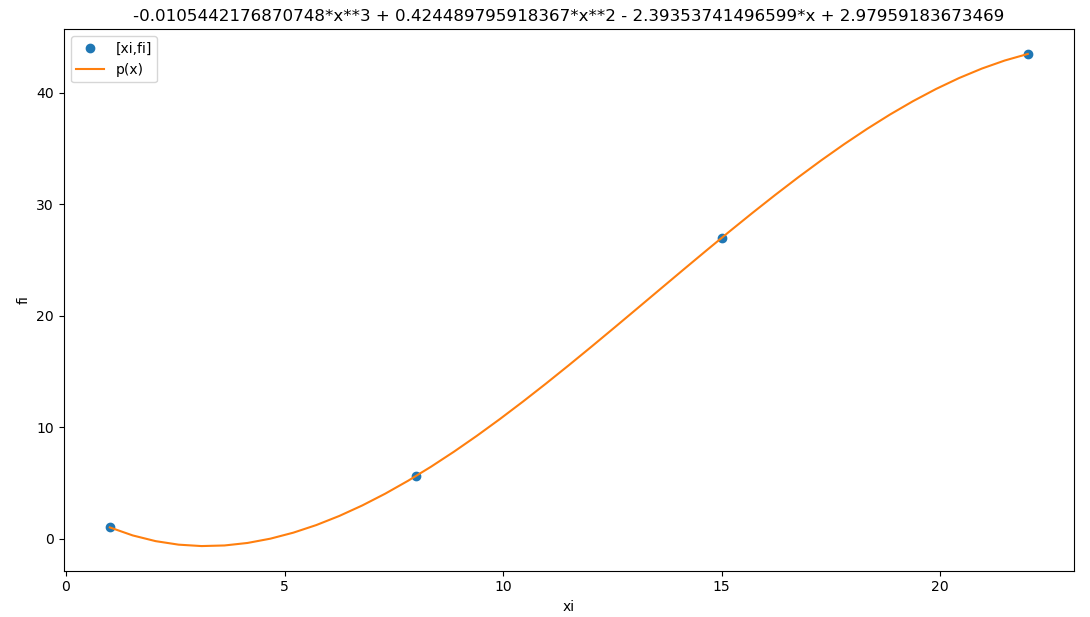
Para analizar el comportamiento de la variable de temperatura, se requiere disponer de un modelo polinomial que describa la temperatura a lo largo del día, para un solo día.

Como valores de variable independiente utilice un equivalente numérico decimal de la hora, minuto y segundo.

a. Realice la lectura del archivo, puede usar las instrucciones descritas en el enlace: Archivos.csv con Python – Ejercicio con gráfica de temperatura y Humedad (CCPG1001: Fundamentos de programación)

b. Seleccione los datos del día 1 del mes para realizar la gráfica, y convierta tiempo en equivalente decimal.

c. Mediante pruebas, determine el grado del polinomio más apropiado para minimizar los errores.

Desarrollo

literal a

Se empieza con las instrucciones del enlace dadas añadiendo los parpametros de entrada como undia = 0 y grado del polinomio como gradom = 2 como el ejercicio anterior.

literal b

En el modelo polinomial, el eje x es un número decimal, por lo que los valores de hora:minuto:segundo se convierte a un valor decimal. Para el valor decimal de xi se usa la unidad de horas y las fracciones proporcionales de cada minuto y segundo.

literal c

Se inicia con el valor de gradom = 2, observando el resultado se puede ir incrementando el grado del polinomio observando los parámetros de error y coeficiente de determinación hasta cumplir con la tolerancia esperada segun la aplicación del ejercicio.

Resultados obtenidos:

columnas en tabla: 
Index(['No', 'Date', 'Time', 'ColdJunc0', 'PowerVolt', 'PowerKind', 'WS(ave)',
       'WD(ave)', 'WS(max)', 'WD(most)', 'WS(inst_m)', 'WD(inst_m)',
       'Max_time', 'Solar_rad', 'TEMP', 'Humidity', 'Rainfall', 'Bar_press.',
       'Soil_temp', 'fecha', 'horadec'],
      dtype='object')
ymedia =  25.036805555555553
 f = -6.57404678141012e-6*x**6 + 0.00052869201494877*x**5 - 0.0152875582352169*x**4 + 0.184200388015364*x**3 - 0.761164009032398*x**2 + 0.393278389794015*x + 22.1142936414255
coef_determinacion r2 =  0.9860621424061621
98.61% de los datos
     se describe con el modelo

Instrucciones en Python

# lecturas archivo.csv de estación meteorológica
import numpy as np
import sympy as sym
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.dates import DateFormatter, DayLocator

# INGRESO
narchivo = "2021OctubreEstMetorologica.csv"
sensor = 'TEMP'
undia  = 2 # dia a revisar
gradom = 6 # grado del polinomio

# PROCEDIMIENTO
tabla = pd.read_csv(narchivo, sep=';',decimal=',')
n_tabla = len(tabla)

# fechas concatenando columnas de texto
tabla['fecha'] = tabla['Date']+' '+tabla['Time']

# convierte a datetime
fechaformato = "%d/%m/%Y %H:%M:%S"
tabla['fecha'] = pd.to_datetime(tabla['fecha'],
                                format=fechaformato)
# serie por dia, busca indices
diaIndice = [0] # indice inicial
for i in range(1,n_tabla-1,1):
    i0_fecha = tabla['fecha'][i-1]
    i1_fecha = tabla['fecha'][i]
    if i0_fecha.day != i1_fecha.day:
        diaIndice.append(i)
diaIndice.append(len(tabla)-1) # indice final
m = len(diaIndice)

# horas decimales en un día
horadia = tabla['fecha'].dt.hour
horamin = tabla['fecha'].dt.minute
horaseg = tabla['fecha'].dt.second
tabla['horadec'] = horadia + horamin/60 + horaseg/3600

# PROCEDIMIENTO Regresión Polinomial grado m
m = gradom
# Selecciona dia
i0 = diaIndice[undia]
i1 = diaIndice[undia+1]
# valores a usar en regresión
xi = tabla['horadec'][i0:i1]
yi = tabla[sensor][i0:i1]
n  = len(xi)

# llenar matriz a y vector B
k = m + 1
A = np.zeros(shape=(k,k),dtype=float)
B = np.zeros(k,dtype=float)
for i in range(0,k,1):
    for j in range(0,i+1,1):
        coeficiente = np.sum(xi**(i+j))
        A[i,j] = coeficiente
        A[j,i] = coeficiente
    B[i] = np.sum(yi*(xi**i))

# coeficientes, resuelve sistema de ecuaciones
C = np.linalg.solve(A,B)

# polinomio
x = sym.Symbol('x')
f = 0
fetiq = 0
for i in range(0,k,1):
    f = f + C[i]*(x**i)
    fetiq = fetiq + np.around(C[i],4)*(x**i)

fx = sym.lambdify(x,f)
fi = fx(xi)

# errores
ym = np.mean(yi)
xm = np.mean(xi)
errado = fi - yi

sr = np.sum((yi-fi)**2)
syx = np.sqrt(sr/(n-(m+1)))
st = np.sum((yi-ym)**2)

# coeficiente de determinacion
r2 = (st-sr)/st
r2_porcentaje = np.around(r2*100,2)

# SALIDA
print(' columnas en tabla: ')
print(tabla.keys())
print('ymedia = ',ym)
print(' f =',f)
print('coef_determinacion r2 = ',r2)
print(str(r2_porcentaje)+'% de los datos')
print('     se describe con el modelo')

# grafica
plt.plot(xi,yi,'o',label='(xi,yi)')
plt.plot(xi,fi, color='orange', label=fetiq)

# lineas de error
for i in range(i0,i1,1):
    y0 = np.min([yi[i],fi[i]])
    y1 = np.max([yi[i],fi[i]])
    plt.vlines(xi[i],y0,y1, color='red',
               linestyle = 'dotted')

plt.xlabel('xi - hora en decimal')
plt.ylabel('yi - '+ sensor)
plt.legend()
etiq_titulo = sensor+ ' dia '+str(undia)
plt.title(etiq_titulo+': Regresion polinomial grado '+str(m))
plt.show()

Tarea

Determinar el polinomio de regresión para los días 3 y 5, y repetir el proceso para el sensor de Humedad ('Humidity')

Referencia: Archivos.csv con Python – Ejercicio con gráfica de temperatura y Humedad en Fundamentos de Programación

2022-08-05

8.3 Regresión polinomial de grado m con Python
Referencia: Chapra 17.2 p482, Burden 8.1 p501

Una alternativa a usar transformaciones ente los ejes para ajustar las curvas es usar regresión polinomial extendiendo el procedimiento de los mínimos cuadrados.

Suponga que la curva se ajusta a un polinomio de segundo grado o cuadrático
y = a_0 + a_1 x + a_2 x^2 +e
usando nuevamente la suma de los cuadrados de los residuos, se tiene,
S_r = \sum_{i=1}^n (y_i- (a_0 + a_1 x_i + a_2 x_i^2))^2
para minimizar los errores se deriva respecto a cada coeficiente: a₀, a₁, a₂
\frac{\partial S_r}{\partial a_0} = -2\sum (y_i- a_0 - a_1 x_i - a_2 x_i^2) \frac{\partial S_r}{\partial a_1} = -2\sum x_i (y_i- a_0 - a_1 x_i - a_2 x_i^2) \frac{\partial S_r}{\partial a_2} = -2\sum x_i^2 (y_i- a_0 - a_1 x_i - a_2 x_i^2)
Se busca el mínimo de cada sumatoria, igualando a cero la derivada y reordenando, se tiene el conjunto de ecuaciones:
a_0 (n) + a_1 \sum x_i + a_2 \sum x_i^2 = \sum y_i a_0 \sum x_i + a_1 \sum x_i^2 + a_2 \sum x_i^3 =\sum x_i y_i a_0 \sum x_i^2 + a_1 \sum x_i^3 + a_2 \sum x_i^4 =\sum x_i^2 y_i
con incógnitas a₀, a₁ y a₂, cuyos coeficientes se pueden evaluar con los puntos observados. Se puede usar un médoto directo de la unidad 3 para resolver el sistema de ecuaciones Ax=B.
\begin{bmatrix} n & \sum x_i & \sum x_i^2 \\ \sum x_i & \sum x_i^2 & \sum x_i^3 \\ \sum x_i^2 & \sum x_i^3 & \sum x_i^4 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \\ \sum x_i^2 y_i \end{bmatrix}
```
C = np.linalg.solve(A,B)
```
y = C_0 + C_1 x + C_2 x^2
El error estándar se obtiene como:
S_{y/x} = \sqrt{\frac{S_r}{n-(m+1)}}
siendo m el grado del polinomio usado, para el caso presentado m = 2
S_r = \sum{(yi-fi)^2}
S_r es la suma de los cuadrados de los residuos alrededor de la línea de regresión.

x_i y_i (y_i-y_media)² (y_i-f_i)²

... ...

... ...

∑y_i S_t S_r

r^2 = \frac{S_t-S_r}{S_t} S_t = \sum{(yi-ym)^2}
siendo S_t la suma total de los cuadrados alrededor de la media para la variable dependiente y. Este valor es la magnitud del error residual asociado con la variable dependiente antes de la regresión.

El algoritmo se puede desarrollar de forma semejante a la presentada en la sección anterior,

Ejercicio Chapra 17.5 p484

Los datos de ejemplo para la referencia son:
```
xi = [0,   1,    2,    3,    4,   5]
yi = [2.1, 7.7, 13.6, 27.2, 40.9, 61.1]
```
resultado de algoritmo:
```
fx  =  1.86071428571429*x**2 + 2.35928571428571*x + 2.47857142857143
Syx =  1.117522770621316
coef_determinacion r2 =  0.9985093572984048
99.85% de los datos se describe con el modelo
>>> 
```
Instrucciones en Python
```
# regresion con polinomio grado m=2
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
xi = [0,   1,    2,    3,    4,   5]
yi = [2.1, 7.7, 13.6, 27.2, 40.9, 61.1]
m  = 2

# PROCEDIMIENTO
xi = np.array(xi)
yi = np.array(yi)
n  = len(xi)

# llenar matriz a y vector B
k = m + 1
A = np.zeros(shape=(k,k),dtype=float)
B = np.zeros(k,dtype=float)
for i in range(0,k,1):
    for j in range(0,i+1,1):
        coeficiente = np.sum(xi**(i+j))
        A[i,j] = coeficiente
        A[j,i] = coeficiente
    B[i] = np.sum(yi*(xi**i))

# coeficientes, resuelve sistema de ecuaciones
C = np.linalg.solve(A,B)

# polinomio
x = sym.Symbol('x')
f = 0
fetiq = 0
for i in range(0,k,1):
    f = f + C[i]*(x**i)
    fetiq = fetiq + np.around(C[i],4)*(x**i)

fx = sym.lambdify(x,f)
fi = fx(xi)

# errores
ym = np.mean(yi)
xm = np.mean(xi)
errado = fi - yi

sr = np.sum((yi-fi)**2)
syx = np.sqrt(sr/(n-(m+1)))
st = np.sum((yi-ym)**2)

# coeficiente de determinacion
r2 = (st-sr)/st
r2_porcentaje = np.around(r2*100,2)

# SALIDA
print('ymedia = ',ym)
print(' f =',f)
print('coef_determinacion r2 = ',r2)
print(str(r2_porcentaje)+'% de los datos')
print('     se describe con el modelo')

# grafica
plt.plot(xi,yi,'o',label='(xi,yi)')
# plt.stem(xi,yi, bottom=ym)
plt.plot(xi,fi, color='orange', label=fetiq)

# lineas de error
for i in range(0,n,1):
    y0 = np.min([yi[i],fi[i]])
    y1 = np.max([yi[i],fi[i]])
    plt.vlines(xi[i],y0,y1, color='red',
               linestyle = 'dotted')

plt.xlabel('xi')
plt.ylabel('yi')
plt.legend()
plt.title('Regresion polinomial grado '+str(m))
plt.show()
```
2022-08-04
8.2 Regresión por Mínimos cuadrados con Python
Referencia: Chapra 17.1.2 p 469. Burden 8.1 p499

Criterio de ajuste a una línea recta por mínimos cuadrados

Una aproximación de la relación entre los puntos x_i, y_i por medio de un polinomio de grado 1, busca minimizar la suma de los errores residuales de los datos.
y_{i,modelo} = p_1(x) = a_0 + a_1 x_i
Se busca el valor mínimo para los cuadrados de las diferencias entre los valores de y_i con la línea recta.

S_r = \sum_{i=1}^{n} \Big( y_{i,medida} - y_{i,modelo} \Big)^2 S_r= \sum_{i=1}^{n} \Big( y_{i} - (a_0 + a_1 x_i) \Big)^2
para que el error acumulado sea mínimo, se deriva respecto a los coeficientes de la recta a₀ y a₁ y se iguala a cero,
\frac{\partial S_r}{\partial a_0}= (-1)2 \sum_{i=1}^{n} \Big( y_{i} - a_0 - a_1 x_i \Big) \frac{\partial S_r}{\partial a_1}= (-1)2 \sum_{i=1}^{n} \Big( y_{i} - a_0 - a_1 x_i \Big)x_i 0 = \sum_{i=1}^{n} y_i - \sum_{i=1}^{n} a_0 - \sum_{i=1}^{n} a_1 x_i 0= \sum_{i=1}^{n} y_i x_i - \sum_{i=1}^{n} a_0x_i - \sum_{i=1}^{n} a_1 x_i^2
simplificando,
\sum_{i=1}^{n} a_0 + a_1 \sum_{i=1}^{n} x_i = \sum_{i=1}^{n} y_{i} a_0 \sum_{i=1}^{n} x_i + a_1 \sum_{i=1}^{n} x_i^2 = \sum_{i=1}^{n} y_i x_i
que es un conjunto de dos ecuaciones lineales simultaneas con dos incógnitas a₀ y a₁, los coeficientes del sistema de ecuaciones son las sumatorias que se obtienen completando la siguiente tabla:

Tabla de datos y columnas para ∑ en la fórmula

x_i y_i x_iy_i x_i² y_i²

x₀ y₀ x₀y₀ x₀² y₀²

... ...

... ...

∑ x_i ∑ y_i ∑ x_iy_i ∑ x_i² ∑ y_i²

\begin{bmatrix} n & \sum x_i \\ \sum x_i & \sum x_i^2 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \end{bmatrix} = \begin{bmatrix} \sum y_i \\ \sum x_i y_i \end{bmatrix}
cuya solución es:
a_1 = \frac{n \sum x_i y_i - \sum x_i \sum y_i}{n \sum x_i^2 - \big( \sum x_i \big) ^2 } a_0 = \overline{y} - a_1 \overline{x}
usando la media de los valores en cada eje para encontrar a₀

Coeficiente de correlación

El coeficiente de correlación se puede obtener con las sumatorias anteriores usando la siguiente expresión:
r= \frac{n \sum x_i y_i - \big( \sum x_i \big) \big( \sum y_i\big)} {\sqrt{n \sum x_i^2 -\big(\sum x_i \big) ^2 }\sqrt{n \sum y_i^2 - \big( \sum y_i \big)^2}}
En un ajuste perfecto, S_r = 0 y r = r² = 1, significa que la línea explica
el 100% de la variabilidad de los datos.

Aunque el coeficiente de correlación ofrece una manera fácil de medir la bondad del ajuste, se deberá tener cuidado de no darle más significado del que ya tiene.

El solo hecho de que r sea “cercana” a 1 no necesariamente significa que el ajuste sea “bueno”. Por ejemplo, es posible obtener un valor relativamente alto de r cuando la relación entre y y x no es lineal.

Los resultados indicarán que el modelo lineal explicó r² % de la incertidumbre original

Algoritmo en Python

Siguiendo con los datos propuestos del ejemplo en Chapra 17.1 p470:
```
xi = [1, 2, 3, 4, 5, 6, 7] 
yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]
```
Aplicando las ecuaciones para a₀ y a₁ se tiene el siguiente resultado para los datos de prueba:
```
 f =  0.839285714285714*x + 0.0714285714285712
coef_correlación   r  =  0.9318356132188194
coef_determinación r2 =  0.8683176100628931
86.83% de los datos está descrito en el modelo lineal
>>>
```
con las instrucciones:
```
# mínimos cuadrados, regresión con polinomio grado 1
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
xi = [1,   2,   3,  4,  5,   6, 7]
yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]

# PROCEDIMIENTO
xi = np.array(xi,dtype=float)
yi = np.array(yi,dtype=float)
n  = len(xi)

# sumatorias y medias
xm  = np.mean(xi)
ym  = np.mean(yi)
sx  = np.sum(xi)
sy  = np.sum(yi)
sxy = np.sum(xi*yi)
sx2 = np.sum(xi**2)
sy2 = np.sum(yi**2)

# coeficientes a0 y a1
a1 = (n*sxy-sx*sy)/(n*sx2-sx**2)
a0 = ym - a1*xm

# polinomio grado 1
x = sym.Symbol('x')
f = a0 + a1*x

fx = sym.lambdify(x,f)
fi = fx(xi)

# coeficiente de correlación
numerador = n*sxy - sx*sy
raiz1 = np.sqrt(n*sx2-sx**2)
raiz2 = np.sqrt(n*sy2-sy**2)
r = numerador/(raiz1*raiz2)

# coeficiente de determinacion
r2 = r**2
r2_porcentaje = np.around(r2*100,2)

# SALIDA
# print('ymedia =',ym)
print(' f = ',f)
print('coef_correlación   r  = ', r)
print('coef_determinación r2 = ', r2)
print(str(r2_porcentaje)+'% de los datos')
print('     está descrito en el modelo lineal')

# grafica
plt.plot(xi,yi,'o',label='(xi,yi)')
# plt.stem(xi,yi,bottom=ym,linefmt ='--')
plt.plot(xi,fi, color='orange',  label=f)

# lineas de error
for i in range(0,n,1):
    y0 = np.min([yi[i],fi[i]])
    y1 = np.max([yi[i],fi[i]])
    plt.vlines(xi[i],y0,y1, color='red',
               linestyle ='dotted')
plt.legend()
plt.xlabel('xi')
plt.title('minimos cuadrados')
plt.show()
```
Coeficiente de correlación con Numpy

Tambien es posible usar la librería numpy para obtener el resultado anterior,
```
>>> coeficientes = np.corrcoef(xi,yi)
>>> coeficientes
array([[1.        , 0.93183561],
       [0.93183561, 1.        ]])
>>> r = coeficientes[0,1]
>>> r
0.9318356132188195
```
2022-08-03
8.1 Regresión vs interpolación
Referencia: Chapra 17.1 p 466. Burden 8.1 p498

Cuando los datos de un experimento presentan variaciones o errores sustanciales respecto al modelo matemático, la interpolación polinomial presentada en la Unidad 4 es inapropiada para predecir valores intermedios.

En el ejemplo de Chapra 17.1 p470, se presentan los datos de un experimento mostrados en la imagen y la siguiente tabla:
```
xi = [1,   2,   3,  4,  5,   6, 7]
yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]
```
Un polinomio de interpolación, por ejemplo de Lagrange de grado 6 pasará por todos los puntos, pero oscilando.

Una función de aproximación que se ajuste a la tendencia general, que no necesariamente pasa por los puntos de muestra puede ser una mejor respuesta. Se busca una "curva" que minimice las diferencias entre los puntos y la curva, llamada regresión por mínimos cuadrados.

Descripción con la media yi

Considere una aproximación para la relación entre los puntos x_i, y_i como un polinomio, grado 0 que sería la media de y_i. Para este caso, los errores se presentan en la gráfica:

Otra forma sería aproximar el comportamiento de los datos es usar un polinomio de grado 1. En la gráfica se pueden observar que para los mismos puntos el error disminuye considerablemente.

El polinomio de grado 1 recibe el nombre de regresión por mínimos cuadrados, que se desarrolla en la siguiente sección.

Instrucciones Python
```
# representación con la media
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
xi = [1,   2,   3,  4,  5,   6, 7]
yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]

# PROCEDIMIENTO
xi = np.array(xi,dtype=float)
yi = np.array(yi,dtype=float)
n = len(xi)

xm = np.mean(xi)
ym = np.mean(yi)

# SALIDA
print('ymedia = ', ym)

# grafica
plt.plot(xi,yi,'o',label='(xi,yi)')
plt.stem(xi,yi,bottom=ym, linefmt = '--')
plt.xlabel('xi')
plt.ylabel('yi')
plt.legend()
plt.show()
```
Instrucciones Python - compara interpolación y regresión.

Para ilustrar el asunto y para comparar los resultados se usa Python, tanto para interpolación y mínimos cuadrados usando las librerías disponibles. Luego se desarrolla el algoritmo paso a paso.
```
# mínimos cuadrados
import numpy as np
import scipy.interpolate as sci
import matplotlib.pyplot as plt

# INGRESO
xi = [1,   2,   3,  4,  5,   6, 7]
yi = [0.5, 2.5, 2., 4., 3.5, 6, 5.5]

# PROCEDIMIENTO
xi = np.array(xi)
yi = np.array(yi)
n = len(xi)

# polinomio Lagrange
px = sci.lagrange(xi,yi)
xj = np.linspace(min(xi),max(xi),100)
pj = px(xj)

# mínimos cuadrados
A = np.vstack([xi, np.ones(n)]).T
[m0, b0] = np.linalg.lstsq(A, yi, rcond=None)[0]
fx = lambda x: m0*(x)+b0
fi = fx(xi)

# ajusta límites
ymin = np.min([np.min(pj),np.min(fi)])
ymax = np.max([np.max(pj),np.max(fi)])

# SALIDA
plt.subplot(121)
plt.plot(xi,yi,'o',label='(xi,yi)')
plt.plot(xj,pj,label='P(x) Lagrange')
plt.ylim(ymin,ymax)
plt.xlabel('xi')
plt.ylabel('yi')
plt.title('Interpolación Lagrange')

plt.subplot(122)
plt.plot(xi,yi,'o',label='(xi,yi)')
plt.plot(xi,fi,label='f(x)')
plt.ylim(ymin,ymax)
plt.xlabel('xi')
plt.title('Mínimos cuadrados')

plt.show()
```
2022-08-02
s1Eva_2022PAOI_T3 Interpolar crecimiento de contagios
Ejercicio: 1Eva_2022PAOI_T3 Interpolar crecimiento de contagios

Día del mes 1 8 15 22

Contagios 1 5.6 27 43.5

a) Realice el planteamiento del sistema de ecuaciones que se usaría usando el método de interpolación polinómica.

El modelo de polinomio de grado máximo que se puede obtener es grado 3:
p_3(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3
por lo que usando los valores de los puntos dados en la tabla:
p_3(1) = a_0 + a_1 (1) + a_2 (1)^2 + a_3 (1)^3 = 1 p_3(8) = a_0 + a_1 (8) + a_2 (8)^2 + a_3 (8)^3 = 5.6 p_3(15) = a_0 + a_1 (15) + a_2 (15)^2 + a_3 (15)^3 = 27 p_3(22) = a_0 + a_1 (22) + a_2 (22)^2 + a_3 (22)^3 = 43.5
b) Realice el planteamiento del sistema de ecuaciones en su forma matricial y muestre la matriz aumentada.
\begin{pmatrix} 1 & 1 & 1^2 & 1^2\\ 1 & 8 & 8^2 & 8^3 \\ 1 & 15 & 15^2 & 15^3 \\ 1 & 22 & 22^2 & 22^3 \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{pmatrix} \begin{pmatrix} 1 \\ 56 \\ 27 \\43.5 \end{pmatrix}
matriz aumentada,
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1 & 8 & 8^2 & 8^3 & 56 \\ 1 & 15 & 15^2 & 15^3 & 27\\ 1 & 22 & 22^2 & 22^3 & 43.5\end{pmatrix}
c) Desarrolle el pivoteo parcial por filas, indicando las operaciones realizadas en éste proceso

pivoteo parcial por filas
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1 & 22 & 22^2 & 22^3 & 43.5 \\ 1 & 15 & 15^2 & 15^3 & 27 \\ 1 & 8 & 8^2 & 8^3 & 56\end{pmatrix}
d) Usando el método directo de Gauss-Jordan, muestre las expresiones necesarias para el algoritmo.

eliminación hacia adelante
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1-1 & 22-1 & 22^2-1^2 & 22^3 -1^3& 43.5 - 1\\ 1-1 & 15-1 & 15^2 -1^2& 15^3 -1^3& 27 -1\\ 1-1 & 8-1 & 8^2 -1^2& 8^3 -1^3& 56-1\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 14 & 224 & 3376& 26\\ 0 & 7 & 63& 511 & 55\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 14-\frac{14}{21} 21 & 224-\frac{14}{21}483& 3376 -\frac{14}{21}10647& 26-\frac{14}{21}42.5\\ 0 & 7-\frac{7}{21}21 & 63-\frac{7}{21}483& 511-\frac{7}{21}10647 & 55-\frac{7}{21}42.5\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & -98 & -3038 & 40.83 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & -98-\frac{98}{-98}98 & -3038 -\frac{98}{-98}3722& 40.83 -\frac{98}{-98}(-2.33)\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & 0 & 686 & -7.23\end{pmatrix}
realizando el proceso de eliminación hacia atrás, semejante al método anterior se obtiene
\begin{pmatrix} 1 & 0 & 0 & 0 & 2.98\\ 0 & 1 & 0 & 0& -2.39 \\ 0 & 0 & 1 & 0 & 0.424 \\ 0 & 0 & 0 &1 & -0.0105\end{pmatrix}
con lo que el vector resultado es:
X= [2.98, -2.39, 0.42, -0.0105]
El polinomio de interpolación resultante es:
p(t)= 2.98 -2.39 t + 0.42 t^2 -0.0105 t^3

e) Para el día 19 se encuentra que el valor correspondiente a contagios es de 37%. Estime el error presentado del modelo para ese día.
p(19)= 2.98 -2.39 (19) + 0.42 (19)^2 -0.0105 (19)^3 = 38.42 error = |38.42-37| = 1.42
f) Desarrolle el ejercicio usando otro método para encontrar el polinomio de interpolación.

usando diferencias finitas
```
Tabla Diferencia Finita
[['i', 'xi', 'fi', 'df1', 'df2', 'df3', 'df4']]
[[  0.    1.    1.    4.6  16.8 -21.7   0. ]
 [  1.    8.    5.6  21.4  -4.9   0.    0. ]
 [  2.   15.   27.   16.5   0.    0.    0. ]
 [  3.   22.   43.5   0.    0.    0.    0. ]]
```
polinomio:
p(t) = 1+\frac{4.6}{1! (7)}(t-1) + + \frac{16.8}{2!(7^2)}(t-1)(t-8) + +\frac{-21.7}{3!(7^3}(t-1)(t-8)(t-15)
Algoritmo en Python

Para literal f
```
# Polinomio interpolación
# Diferencias finitas avanzadas
# Tarea: Verificar tamaño de vectores,
#        verificar puntos equidistantes en x

import numpy as np
import math
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO , Datos de prueba
xi = np.array([1,8,15,22],dtype=float)
fi = np.array([1,5.6,27,43.5],dtype=float)

# PROCEDIMIENTO

# Tabla de Diferencias Finitas
titulo = ['i','xi','fi']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)

# diferencias finitas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)

# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
    # Añade título para cada columna
    titulo.append('df'+str(j-2))
    # cada fila de columna
    i = 0
    while (i < diagonal):
        tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1]
        i = i+1
    diagonal = diagonal - 1
    j = j+1

# POLINOMIO con diferencias Finitas avanzadas
# caso: puntos equidistantes en eje x
h = xi[1] - xi[0]
dfinita = tabla[0,3:]
n = len(dfinita)

# expresión del polinomio con Sympy
x = sym.Symbol('x')
polinomio = fi[0]
for j in range(1,n,1):
    denominador = math.factorial(j)*(h**j)
    factor = dfinita[j-1]/denominador
    termino = 1
    for k in range(0,j,1):
        termino = termino*(x-xi[k])
    polinomio = polinomio + termino*factor

# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()

# polinomio para evaluacion numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
print('Tabla Diferencia Finita')
print([titulo])
print(tabla)
print('dfinita: ')
print(dfinita)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)

# Gráfica
plt.plot(xi,fi,'o', label = 'Puntos')
##for i in range(0,n,1):
##    plt.axvline(xi[i],ls='--', color='yellow')
plt.plot(pxi,pfi, label = 'Polinomio')

plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Interpolación polinómica')
plt.show()
```
2022-07-10
s1Eva_2022PAOI_T2 Capacidad de alimentos para pacientes internos
Ejercicio: 1Eva_2022PAOI_T2 Capacidad de alimentos para pacientes internos

a) Realice el planteamiento del sistema de ecuaciones que permita determinar la cantidad máxima de pacientes de cada grupo que podrían ser atendidos usando todos los productos disponibles. Una vez planteadas las ecuaciones, se le indica que la capacidad de atención para emergencia sea fija en K = 10 pacientes (variable libre).

Producto\ Paciente Maternidad Pos - operatorio Covid_19 emergencia Suministro diario

Producto A 0.2 0.1 1.7 0.25 135

Producto B 0.5 2 0.05 0.4 320

Producto C 1.5 0.2 0.75 1.4 410

Sistema de ecuaciones usando la columna de emergencias como variable libre y valor constante para la variable igual a K=10
0.2 x_1 + 0.1 x_2 +1.7 x_3 = 135-0.25 K 0.5 x_1 + 2 x_2 +0.05 x_3 = 320-0.4 K 1.5 x_1 + 0.2 x_2 +0.75 x_3 = 410-1.4 K
b) Muestre los pasos detallados para la matriz aumentada y pivoteo parcial por filas.

matriz aumentada
\begin{pmatrix} 0.2 & 0.1 & 1.7 & 135-0.25*10 \\ 0.5 & 2 &0.05 & 320-0.4*10 \\ 1.5 & 0.2 & 0.75 &410-1.4*10 \end{pmatrix}
pivoteo parcial por filas
\begin{pmatrix} 1.5 & 0.2 & 0.75 & 396 \\ 0.5 & 2 &0.05 & 316 \\ 0.2 & 0.1 & 1.7 & 132.5 \end{pmatrix}
c) Desarrolle al menos 3 iteraciones para el método requerido, con expresiones completas.
$1.5 x_1 + 0.2 x_2 +0.75 x_3 = 396$
0.5 x_1 + 2 x_2 +0.05 x_3 = 316 0.2 x_1 + 0.1 x_2 +1.7 x_3 = 132.5
ecuaciones a usar
x_1 = \frac{1}{1.5}(396 - 0.2 x_2 - 0.75 x_3) x_2 = \frac{1}{2}(316 - 0.5 x_1 - 0.05 x_3) x_3 = \frac{1}{1.7}(132.5 - 0.2 x_1 - 0.1 x_2)
Dado que el valor de la variable libre se establecía con K=10, el vector inicial podría ser el doble de este valor
X_0 = [20,20,20]
itera=1
X_0 = [20,20,20] x_1 = \frac{1}{1.5}(396 - 0.2(20) - 0.75(20)) =251.33 x_2 = \frac{1}{2}(316 - 0.5(20) - 0.05 (20)) = 152.5 x_3 = \frac{1}{1.7}(132.5 - 0.2 (20) - 0.1 (20)) =74.41 diferencia = [231.33, 132.5, 54.41] errado = max |[231.33, 132.5, 54.41]| = 231.33
itera=2
X_1 = [251.33, 152.5, 74.41] x_1 = \frac{1}{1.5}(396 - 0.2(152.5) - 0.75(74.41)) =206.46 x_2 = \frac{1}{2}(316 - 0.5(251.33) - 0.05 (74.41)) = 96.30 x_3 = \frac{1}{1.7}(132.5 - 0.2 (251.33) - 0.1 (152.5)) =39.40 diferencia = [-44.86, -59.27, -211.92] errado = max |[-44.86, -59.27, -211.92]| = 211.92
itera=3
X_2 = [231.85, 105.39, 48.16] x_1 = \frac{1}{1.5}(396 - 0.2(105.39) - 0.75(48.16)) =231.85 x_2 = \frac{1}{2}(316 - 0.5(231.85) - 0.05 (48.16)) = 105.39 x_3 = \frac{1}{1.7}(132.5 - 0.2 ( 231.85) - 0.1 (105.39)) =48.16 diferencia = [25.39, 121.09, -158.29] errado = max |[25.39, 121.09, -158.29]| = 158.29 X_3 = [231.85, 105.39, 48.16]
d) Realice las observaciones necesarias sobre los errores entre iteraciones y la convergencia.

El error entre iteraciones disminuye, el método converge a:
```
respuesta X: 
[[228.22]
 [ 99.81]
 [ 44.92]]
```
e) Si se decide no atender a los pacientes del grupo emergencias, ¿Qué aumento individual de cada una de otros grupos de pacientes podría soportarse con la cantidad diaria de alimento disponible? (use el algoritmo.py).

Se interpreta como K=0 y usando el algoritmo se obtiene:
```
respuesta X: 
[[237.23]
 [ 99.54]
 [ 45.64]]
```
el aumento de pacientes entre grupos es
```
diferencia = [9.01, -0.27, 0.72]
```
en términos de pacientes, como número entero, solo se gana 9 pacientes para el primer grupo. Se descarta la parte decimal si los pacientes no se cuentan en miles, por lo que las otras variaciones se interpretan como cero.

Algoritmo en Python

Datos tomados luego de pivoteo parcial por filas

Resultados:
```
0 [20. 20. 20.]
0 [251.33333333 152.5         74.11764706]
1 [206.60784314  93.31372549  39.10784314]
2 [232.00424837 105.37034314  47.85121107]
3 [226.02501538  98.80265763  44.15418589]
4 [228.74921937 100.38989151  45.24395951]
5 [227.99270138  99.68159617  44.83009822]
6 [228.2940714   99.8810722   44.96076477]
7 [228.20214132  99.80246303  44.91357559]
8 [228.23621714  99.82662528  44.92901496]
9 [228.22527582  99.81772034  44.92358473]
10 [228.22917825  99.82059143  44.92539577]
11 [228.22788993  99.81957054  44.92476777]
12 [228.22834004  99.81990832  44.92497939]
13 [228.2281892   99.8197905   44.92490656]
14 [228.22824132  99.81983004  44.92493124]
numero de condicion: 2.166985328561448
respuesta con Jacobi
[[228.22824132]
 [ 99.81983004]
 [ 44.92493124]]
verificando:
[[396.00002641]
 [316.00002729]
 [132.00001438]]
```
Algoritmo en Python
```
# 1Eva_2022PAOI_T2 Capacidad de alimentos para pacientes internos
import numpy as np

def jacobi(A,B,tolera,X,iteramax=100):
    tamano = np.shape(A)
    n = tamano[0]
    m = tamano[1]
    diferencia = np.ones(n, dtype=float)
    errado = np.max(diferencia)
    xnuevo = np.copy(X)

    itera = 0
    print(itera, X)
    while not(errado<=tolera or itera>iteramax):
        
        for i in range(0,n,1):
            nuevo = B[i]
            for j in range(0,m,1):
                if (i!=j): # excepto diagonal de A
                    nuevo = nuevo-A[i,j]*X[j]
            nuevo = nuevo/A[i,i]
            xnuevo[i] = nuevo
        diferencia = np.abs(xnuevo-X)
        errado = np.max(diferencia)
        print(itera, xnuevo)
        X = np.copy(xnuevo)
        itera = itera + 1
    # Vector en columna
    X = np.transpose([X])
    # No converge
    if (itera>iteramax):
        X=itera
    return(X)


# INGRESO
A = np.array([[1.5, 0.2, 0.75],
              [0.5, 2.0, 0.05],
              [0.2, 0.1, 1.7 ]],
             dtype=float)

B = np.array([396.,316.,132.],
             dtype=float)
tolera = 1e-4

X = np.array([20.,20.,20.],
             dtype=float)

# PROCEDIMIENTO

# numero de condicion
ncond = np.linalg.cond(A)

respuesta = jacobi(A,B,tolera,X)

verifica = np.dot(A,respuesta)

# SALIDA
print('numero de condicion:', ncond)
print('respuesta con Jacobi')
print(respuesta)
print('verificando:')
print(verifica)
```
2022-07-10
s1Eva_2022PAOI_T1 Impacto en trayectoria del drone
Ejercicio: 1Eva_2022PAOI_T1 Impacto en trayectoria del drone

Desarrollo analítico

a) Realice el planteamiento del problema usando inicialmente las trayectorias en el eje x, donde para el intervalo de operación del misil antidrone, se observa más de un impacto.

x₁(t) = x₂(t)

f(t) = cos(t) - sin(0.75 t) =0

y₁(t) = y₂(t)

sin(2 t) =kt
k = \frac{sin(2 t)}{t}
b) Usando el método de Newton-Raphson encuentre el valor de t en el cual se pretende realizar el impacto al drone. Realice al menos 3 iteraciones de forma analítica, use tolerancia de 10^-4,
f(t) = cos(t) - sin(0.75 t) f'(t) = - sin(t) - 0.75 cos(0.75 t)

Como punto inicial para encontrar la raíz de f(t) podría ser t₀=4 para el punto marcado en rojo. Para el método de Newton-Raphson se tiene que
t_{i+1} = t_i - \frac{f(t_i)}{f'(t_i)} error = |t_{i+1} - t_i|
iteración 1 t₀=4
t_1 = 4 - \frac{cos(4) - sin(0.75*4)}{- sin(4) - 0.75 cos(0.75*4)} t_1 = 4 - \frac{-0.7947}{1.4992} = 4.5300 tramo = |4.5300-4| = 0.53
iteración 2 t₁=4.53
t_{2} = 4.53 - \frac{cos(4.53) - sin(0.75*4.53)}{- sin(4.53) - 0.75 cos(0.75*4.53)} t_2 = 4.53 - \frac{-0.0717}{1.7089} = 4.4880 tramo= |4.4880-4.53| = 0.042
iteración 3 t₂=4.4880
t_{3} = 4.4880 - \frac{cos(4.4880) - sin(0.75*4.4880)}{ - sin(4.4880) - 0.75 cos(0.75*4.4880)} t_3 = 4.4880 - \frac{-0.0000179}{1.7061} = 4.4879 tramo= |4.4879-4.4880| = 0.0001
c) Realice el análisis de la convergencia del método.

El error disminuye, el método converge. La raiz se encuentra en t=4.487989505154422

d) Con el resultado de t anterior, determine el valor de la constante k para la expresión de y₂(t) que asegura el impacto contra el drone.
y_1(t) = y_2(t) sin(2 t) =kt k = \frac{sin(2 t)}{t} = \frac{sin(2*4.487989505154422)}{4.487989505154422} = 0.096714
Desarrollo con Algoritmo

Resultados
```
['xi', 'xnuevo', 'tramo']
[[4.0000e+00 4.5301e+00 5.3009e-01]
 [4.5301e+00 4.4880e+00 4.2071e-02]
 [4.4880e+00 4.4880e+00 3.0277e-05]]
raiz en:  4.487989505154422
con error de:  3.0276981949128867e-05
```
Algoritmo en Python
```
# Método de Newton-Raphson
import numpy as np

# INGRESO
fx  = lambda t: np.cos(1*t) - np.sin(0.75*t)
dfx = lambda t: -np.sin(t) - np.cos(0.75*t)*0.75

x0 = 4
tolera = 0.0001

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)
```
2022-07-10
1Eva_2022PAOI_T3 Interpolar crecimiento de contagios

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

Tema 3. (35 puntos). Según los reportes epidemiológicos para el mes de junio-2022, se presenta un aumento de resultados positivos de COVID-19.

Un médico especialista indica que entre los motivos para transmisión y contagio se encuentran que no se usan las mascarilla y las aglomeraciones como las presentadas durante el paro nacional.

Para las últimas semanas, los resultados han pasado desde 1%, 5.6 %, 27 % y hasta 43.5 %.

Día del mes 1 8 15 22

Contagios 1 5.6 27 43.5

Para un análisis de comportamiento de contagios durante el mes, se requiere disponer de un polinomio de interpolación de grado 3 que describa el comportamiento de los contagios.

a) Realice el planteamiento del sistema de ecuaciones que se usaría usando el método de interpolación polinómica.

b) Realice el planteamiento del sistema de ecuaciones en su forma matricial y muestre la matriz aumentada.

c) Desarrolle el pivoteo parcial por filas, indicando las operaciones realizadas en éste proceso

d) Usando el método directo de Gauss-Jordan, muestre las expresiones necesarias para el algoritmo.

e) Para el día 19 se encuentra que el valor correspondiente a contagios es de 37%. Estime el error presentado del modelo para ese día.

f) Desarrolle el ejercicio usando otro método para encontrar el polinomio de interpolación.

Rúbrica: literal a (5 puntos), literal b (2 puntos), literal c (5 puntos), eliminación hacia adelante (5 puntos), eliminación hacia atrás (5 puntos) literal e (3 puntos), literal f (10 puntos).

Referencias: El nivel de positividad para COVID-19 llega a un 40 %; ingresos hospitalarios son pocos, pero aglomeraciones por el paro ponen en alerta a epidemiólogos. Eluniverso.com 4-julio-2022.

https://www.eluniverso.com/noticias/ecuador/nivel-de-positividad-para-covid-19-llega-a-un-40-ingresos-hospitalarios-son-pocos-pero-aglomeraciones-en-el-paro-indigena-ponen-en-alerta-a-epidemiologos-nota/?modulo=destacadas-dos

Ligero incremento de casos de covid-19 en Ecuador. elcomercio.com 17-mayo-2022. https://www.elcomercio.com/tendencias/sociedad/ligero-incremento-casos-covid19-ecuador.html

2022-07-10
1Eva_2022PAOI_T2 Capacidad de alimentos para pacientes internos

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

Tema 2. (35 puntos). Debido al un “paro nacional” en el país, varios productos de primera necesidad escasean o se encuentran con sobreprecio debido a los cierres de vías de acceso en varias ciudades.

En la entrevista a un representante de los comerciantes de un mercado advirtió que disponían de alimentos almacenados, pero que pronto podrían acabarse si no se reestablecen las vías de acceso para los suministros desde el campo.

En una institución como un hospital, se requiere alimentar a los pacientes internados. Dadas las condiciones, se requiere determinar el número de pacientes que se pueden atender con una cantidad limitada de productos diarios, para al menos tres tipos de dietas y aprovechando todos los ingredientes.

Producto\ Paciente Maternidad Pos - operatorio Covid_19 emergencia Suministro diario

Producto A 0.2 0.1 1.7 0.25 135

Producto B 0.5 2 0.05 0.4 320

Producto C 1.5 0.2 0.75 1.4 410

a) Realice el planteamiento del sistema de ecuaciones que permita determinar la cantidad máxima de pacientes de cada grupo que podrían ser atendidos usando todos los productos disponibles. Una vez planteadas las ecuaciones, se le indica que la capacidad de atención para emergencia sea fija en K = 10 pacientes (variable libre).

Encuentre una solución sistema de ecuaciones con el método Jacobi. (Seleccione un vector inicial).

b) Muestre los pasos detallados para la matriz aumentada y pivoteo parcial por filas.

c) Desarrolle al menos 3 iteraciones para el método requerido, con expresiones completas.

d) Realice las observaciones necesarias sobre los errores entre iteraciones y la convergencia.

e) Si se decide no atender a los pacientes del grupo emergencias, ¿Qué aumento individual de cada una de otros grupos de pacientes podría soportarse con la cantidad diaria de alimento disponible? (use el algoritmo.py).

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (9 puntos), literal d (6 puntos), literal d (5 puntos) literal e (5 puntos)

Referencia: Paro nacional: Cuenca pasa por escasez y sobreprecio de productos de primera necesidad por bloqueos. Eluniverso.com. 15-junio-2022. https://www.eluniverso.com/noticias/ecuador/paro-nacional-cuenca-pasa-por-escasez-y-sobreprecio-de-productos-de-primera-necesidad-por-bloqueos-nota/

Comerciantes intentan tomarse supermercados en Cuenca, debido a desabastecimiento. Vistazo.com 27-junio-2022. https://www.vistazo.com/actualidad/nacional/comerciantes-intentan-tomarse-supermercados-en-cuenca-debido-a-desabastecimiento-FD2063623

Ecuador podrá recuperarse del paro en el segundo semestre de 2022. Primicias.ec 4-julio-2022. https://www.primicias.ec/noticias/economia/ecuador-recuperacion-paro-nacional-segundo-semestre-banco-central/

2022-07-10
1Eva_2022PAOI_T1 Impacto en trayectoria del drone

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

Tema 1 (30 puntos) La trayectoria automática de un drone espía en un territorio de guerra esta descrita por x₁(t), y₁(t).
Drone
x₁(t) = cos(t)
y₁(t) = sin(2 t)

Antidrone
x₂(t) = sin(0.75 t)
y₂(t) = k t

Durante un intervalo de tiempo t entre [0,10] segundos, se dispara un misil antidrone con trayectoria descrita por x₂(t), y₂(t). El antidrone tiene un parámetro de control constante denominado k para y₂(t) que se establece antes del disparo.

Encuentre el valor de k que produce el impacto que destruye el Drone.

Para que se produzca el impacto, deben coincidir las coordenadas x,y para ambas trayectorias, al mismo valor de tiempo.

a) Realice el planteamiento del problema usando inicialmente las trayectorias en el eje x, donde para el intervalo de operación del misil antidrone, se observa más de un impacto.

b) Usando el método de Newton-Raphson encuentre el valor de t en el cual se pretende realizar el impacto al drone. Realice al menos 3 iteraciones de forma analítica, use tolerancia de 10^-4,

c) Realice el análisis de la convergencia del método.

d) Con el resultado de t anterior, determine el valor de la constante k para la expresión de y₂(t) que asegura el impacto contra el drone.

Rúbrica: literal a (5 puntos), iteraciones (9 puntos), errores entre iteraciones(6 puntos), análisis de convergencia(5 puntos), literal d(5 puntos)

Referencia: Domo de Hierro, así funciona el escudo antimisiles de Israel. CNN en español. 15-mayo-2021.

Lo que hay que saber sobre los misiles hipersónicos disparados por Rusia contra Ucrania. cnnespanol.cnn.com 10-mayo-2022. https://cnnespanol.cnn.com/2022/05/10/misiles-hipersonicos-rusia-ucrania-trax/

2022-07-10

x_i	y_i	x_iy_i	x_i²	y_i²
x₀	y₀	x₀y₀	x₀²	y₀²
...	...
...	...
∑ x_i	∑ y_i	∑ x_iy_i	∑ x_i²	∑ y_i²

Producto\ Paciente	Maternidad	Pos - operatorio	Covid_19	emergencia	Suministro diario
Producto A	0.2	0.1	1.7	0.25	135
Producto B	0.5	2	0.05	0.4	320
Producto C	1.5	0.2	0.75	1.4	410

Día del mes	1	8	15	22
Contagios	1	5.6	27	43.5

Día del mes	1	8	15	22
Contagios	1	5.6	27	43.5

Autor: Edison Del Rosario

Desarrollo

literal a

literal b

literal c

Instrucciones en Python

Tarea

Ejercicio Chapra 17.5 p484

Instrucciones en Python

Criterio de ajuste a una línea recta por mínimos cuadrados

Coeficiente de correlación

Algoritmo en Python

Coeficiente de correlación con Numpy

Descripción con la media yi

Instrucciones Python

Instrucciones Python - compara interpolación y regresión.

Algoritmo en Python

Algoritmo en Python

Desarrollo analítico

Desarrollo con Algoritmo

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022

1ra Evaluación 2022-2023 PAO I. 5/Julio/2022