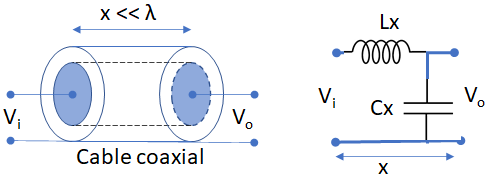
Ejercicio: 2Eva_2021PAOII_T3 EDP – Línea de transmisión sin pérdidas
Desarrollo para determinar el Voltaje v(t),
\frac{\partial ^2 V}{\partial x^2} =LC \frac{\partial ^2 V}{\partial t^2}
0 < x < 200
t>0
Seleccionando diferencias divididas centradas para x y t
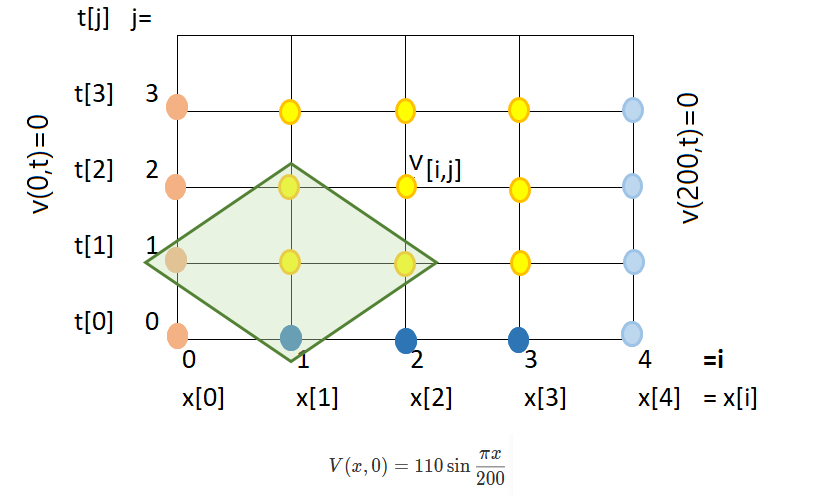
\frac{v_{i,j+1}-2v_{i,j}+v_{i,j-1}}{(\Delta x)^2} =LC \frac{v_{i+1,j}-2v_{i,j}+v_{i-1,j}}{(\Delta t)^2}
agrupando las constantes como lambda,
\frac{(\Delta t)^2}{LC}\frac{v_{i,j+1}-2v_{i,j}+v_{i,j-1}}{(\Delta x)^2} =LC \frac{v_{i+1,j}-2v_{i,j}+v_{i-1,j}}{(\Delta t)^2} \frac{(\Delta t)^2}{LC}
\frac{(\Delta t)^2}{LC(\Delta x)^2} \Big[ v_{i,j+1} -2v_{i,j}+v_{i,j-1} \Big] =v_{i+1,j}-2v_{i,j}+v_{i-1,j}
\lambda = \frac{(\Delta t)^2}{LC(\Delta x)^2}
\lambda = \frac{(0.1)^2}{(0.1)(0.3)(10)^2} = 0.003333
con lo que se comprueba que λ ≤ 1, por lo que el algoritmo es convergente.
Para reducir la cantidad de muestras, se iguala λ = 1, manteniendo el valor de Δx y calculando Δt
\Delta t = \Delta x \sqrt{LC}
\Delta t = 10 \sqrt{0.1(0.3)} = 1.7320
continuando con el valor de λ en la ecuacion general,
\lambda \Big[ v_{i,j+1} -2v_{i,j}+v_{i,j-1} \Big] =v_{i+1,j} -2v_{i,j}+v_{i-1,j}
\lambda v_{i,j+1} +(-2\lambda +2) v_{i,j} + \lambda v_{i,j-1} = v_{i+1,j}+v_{i-1,j}
usando la condición inicial, para j = 0, y diferencias divididas centradas:
\frac{\partial V}{\partial t}(x,0) = 0
\frac{v_{i,1}-v_{i,-1}}{2\Delta t} = 0
v_{i,1}-v_{i,-1} = 0
v_{i,1} = v_{i,-1}
y en la ecuacion del problema, con j = 0
\lambda v_{i,1} +(-2\lambda +2) v_{i,0} + \lambda v_{i,-1} = v_{i+1,0}+v_{i-1,0}
2 \lambda v_{i,1} +(-2\lambda +2) v_{i,0} = v_{i+1,0}+v_{i-1,0}
2 \lambda v_{i,1} = (2\lambda -2) v_{i,0} + v_{i+1,0}+v_{i-1,0}
v_{i,1} = \frac{1}{2 \lambda}\Bigg[ (2\lambda -2) v_{i,0} + v_{i+1,0}+v_{i-1,0} \Bigg]
si λ=1,
v_{i,1} = \frac{v_{i+1,0}+v_{i-1,0}}{2 }
con j =0, i =1
v_{1,1} = \frac{v_{2,0}+v_{0,0}}{2 } =\frac{1}{2}\Big( 110 \sin \frac{\pi(0+2\Delta x) }{200}+0 \Big) =17
con j =0, i =2
v_{2,1} = \frac{v_{3,0}+v_{1,0}}{2 }
v_{2,1} = \frac{1}{2}\Big( 110 \sin \frac{\pi(30) }{200}+110 \sin \frac{\pi(10) }{200} \Big)=33.57
con j =0, i =3
v_{3,1} = \frac{v_{4,0}+v_{2,0}}{2}
v_{2,1} = \frac{1}{2}\Big( 110 \sin \frac{\pi(40) }{200}+110 \sin \frac{\pi(20) }{200} \Big)=49.32
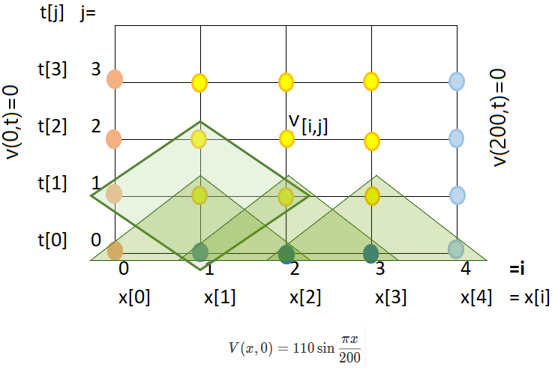
para j>0, se dispone de los valores de los puntos dentro del rombo, excepto v[i,j+1]
\lambda v_{i,j+1} +(-2\lambda +2) v_{i,j} + \lambda v_{i,j-1} = v_{i+1,j}+v_{i-1,j}
\lambda v_{i,j+1} = (2\lambda -2) v_{i,j} - \lambda v_{i,j-1} + v_{i+1,j}+v_{i-1,j}
v_{i,j+1} = \frac{1}{\lambda}\Big( (2\lambda -2) v_{i,j} - \lambda v_{i,j-1} + v_{i+1,j}+v_{i-1,j} \Big)
teniendo como valores de las filas:
u[:,1] = [ 0. , 17. , 33.57, 49.32, 63.86, 76.82, 87.9 , ... ])
u[:,0] = [ 0. , 17.21, 33.99, 49.94, 64.66, 77.78, 88.99, ... ])
con j = 1 ; i = 1 ; (λ=1)
v_{1,2} = \frac{1}{\lambda}\Big( (2\lambda -2) v_{1,1} - \lambda v_{1,0} + v_{2,1}+v_{0,1} \Big)
v_{1,2} = \frac{1}{\lambda}\Big( (2\lambda-2) 17-\lambda 17.21+ 33.57+0\Big)=16.37
con j = 1 ; i = 2 ; (λ=1)
v_{2,2} = \frac{1}{\lambda}\Big( (2\lambda -2) v_{2,1} - \lambda v_{2,0} + v_{3,1}+v_{1,1} \Big)
v_{2,2} = \frac{1}{\lambda}\Big( (2\lambda-2) 33.57-\lambda 33.99+ 49.32+17\Big)=32.33
con j = 1 ; i = 3 ; (λ=1)
v_{2,2} = \frac{1}{\lambda}\Big( (2\lambda -2) v_{3,1} - \lambda v_{3,0} + v_{4,1}+v_{2,1} \Big)
v_{2,2} = \frac{1}{\lambda}\Big( (2\lambda-2) 49.32-\lambda 49.94 + 63.86+33.57\Big)=47.49
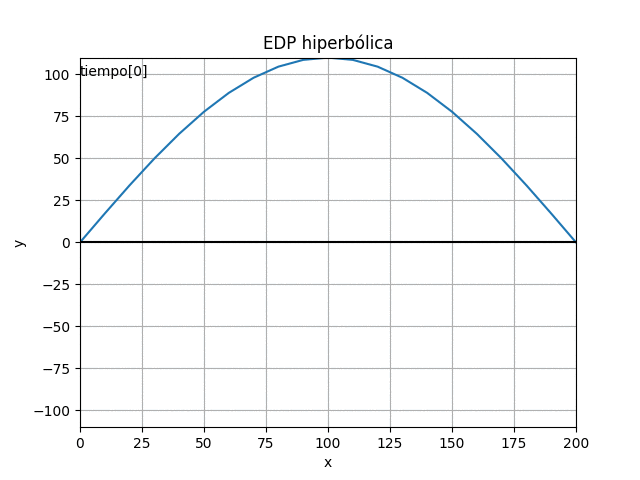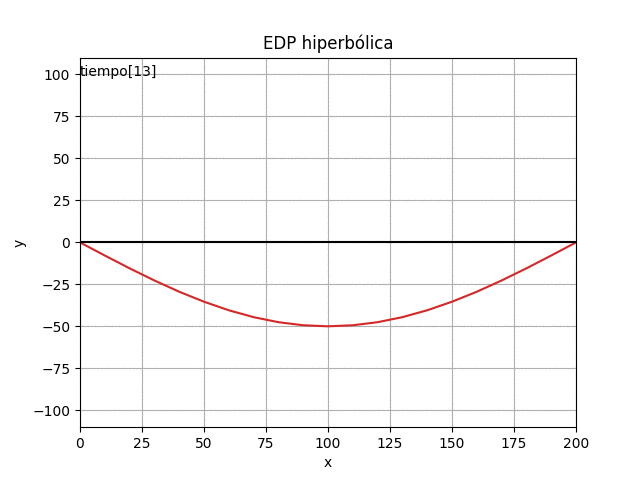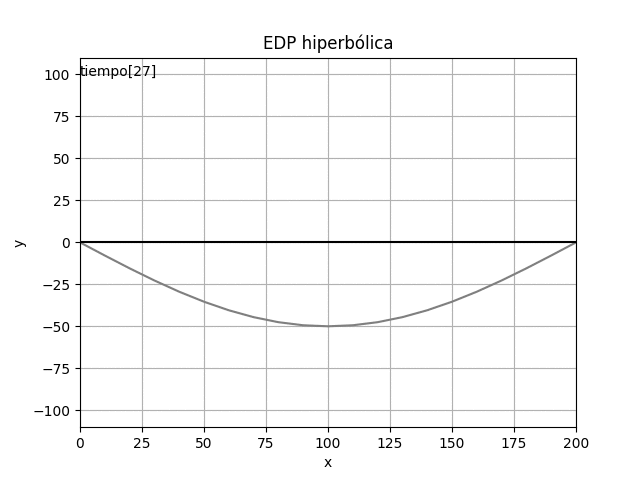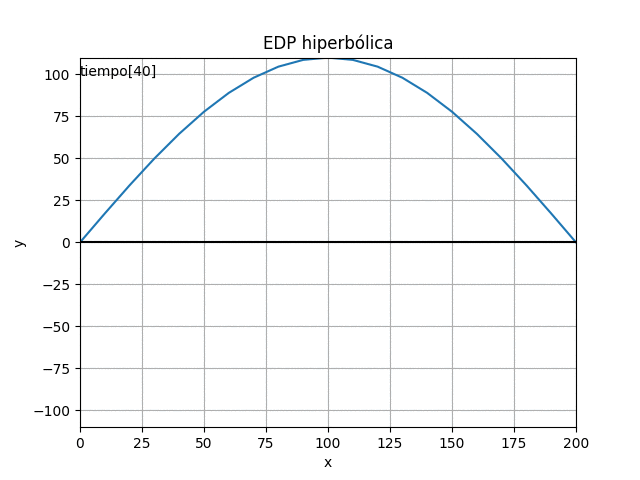
usando el algoritmo con los valores y ecuaciones encontradas se obtiene:
21 41
xi =
[ 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170
180 190 200]
tj =
[ 0. 1.73 3.46 5.2 6.93 8.66 10.39 12.12 13.86 15.59 17.32 19.05
20.78 22.52 24.25 25.98 27.71 29.44 31.18 32.91 34.64 36.37 38.11 39.84
41.57 43.3 45.03 46.77 48.5 50.23 51.96 53.69 55.43 57.16 58.89 60.62
62.35 64.09 65.82 67.55 69.28]
matriz u =
....
Instrucciones en Python
# 2Eva_2021PAOII_T2 EDP – Línea de transmisión sin pérdidas
# Ecuaciones Diferenciales Parciales
# Hiperbólica. Método explicito
import numpy as np
# INGRESO
L = 0.1
C = 0.3
x0 = 0
xn = 200 # Longitud de cable
vx0 = lambda x: 110*np.sin(np.pi*x/200)
y0 = 0
yn = 0 # Puntos de amarre
t0 = 0
tn = 68
# discretiza
dx = 10
dt = dx*np.sqrt(L*C)
# PROCEDIMIENTO
xi = np.arange(x0,xn+dx,dx)
tj = np.arange(0,tn+dt,dt)
n = len(xi)
m = len(tj)
print(n,m)
u = np.zeros(shape=(n,m),dtype=float)
u[:,0] = vx0(xi)
u[0,:] = y0
u[n-1,:] = yn
# calcula lamb
lamb = (dt**2)/(L*C*(dx**2))
# Aplicando condición inicial
j = 0
for i in range(1,n-1,1):
u[i,j+1] = ((2*lamb-2)*u[i,j]+u[i+1,j]+u[i-1,j])/(2*lamb)
# Para los otros puntos
for j in range(1,m-1,1):
for i in range(1,n-1,1):
u[i,j+1] = (1/lamb)*((2*lamb-2)*u[i,j]-lamb*u[i,j-1]+u[i+1,j]+u[i-1,j])
# SALIDA
np.set_printoptions(precision=2)
print('xi =')
print(xi)
print('tj =')
print(tj)
print('matriz u =')
print(u)
# GRAFICA
import matplotlib.pyplot as plt
for j in range(0,m,1):
y = u[:,j]
plt.plot(xi,y)
plt.title('EDP hiperbólica')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# **** GRÁFICO CON ANIMACION ***********
import matplotlib.animation as animation
# Inicializa parametros de trama/foto
retardo = 70 # milisegundos entre tramas
tramas = m
maximoy = np.max(np.abs(u))
figura, ejes = plt.subplots()
plt.xlim([x0,xn])
plt.ylim([-maximoy,maximoy])
# lineas de función y polinomio en gráfico
linea_poli, = ejes.plot(xi,u[:,0], '-')
plt.axhline(0, color='k') # Eje en x=0
plt.title('EDP hiperbólica')
# plt.legend()
# txt_x = (x0+xn)/2
txt_y = maximoy*(1-0.1)
texto = ejes.text(x0,txt_y,'tiempo:',
horizontalalignment='left')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
# Nueva Trama
def unatrama(i,xi,u):
# actualiza cada linea
linea_poli.set_ydata(u[:,i])
linea_poli.set_xdata(xi)
linea_poli.set_label('tiempo linea: '+str(i))
texto.set_text('tiempo['+str(i)+']')
# color de la línea
if (i<=9):
lineacolor = 'C'+str(i)
else:
numcolor = i%10
lineacolor = 'C'+str(numcolor)
linea_poli.set_color(lineacolor)
return linea_poli, texto
# Limpia Trama anterior
def limpiatrama():
linea_poli.set_ydata(np.ma.array(xi, mask=True))
linea_poli.set_label('')
texto.set_text('')
return linea_poli, texto
# Trama contador
i = np.arange(0,tramas,1)
ani = animation.FuncAnimation(figura,
unatrama,
i ,
fargs=(xi,u),
init_func=limpiatrama,
interval=retardo,
blit=True)
# Graba Archivo video y GIFAnimado :
# ani.save('EDP_hiperbólica.mp4')
ani.save('EDP_LineaSinPerdidas.gif', writer='imagemagick')
plt.draw()
plt.show()