Ejercicio: 1Eva_2021PAOII_T1 Interpolación para perfil de terreno
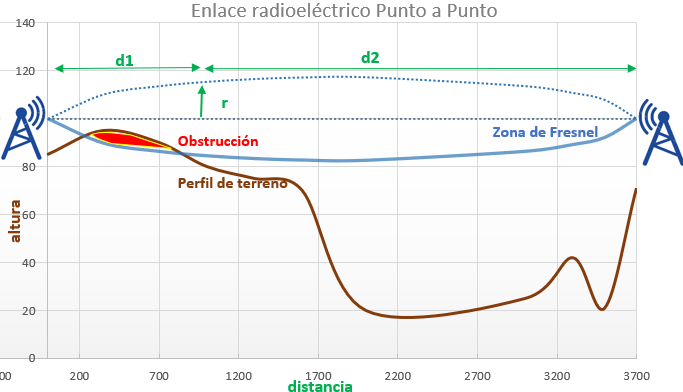
a. Plantee y desarrolle un polinomio P3(d1) de grado 3, que describa el perfil del terreno en el intervalo [0,1300] de distancias a la primera antena d1.
Para plantear el ejercicio, se observan los punto en el intervalo [0,1300], asi como los tamaños de paso.
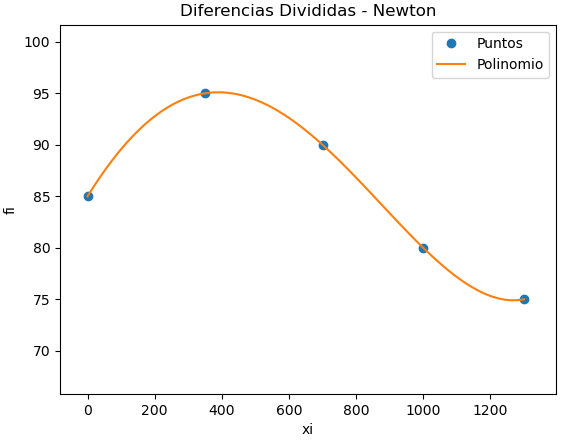
Como el polinomio es de grado 3,se requiere 3 tramos o 4 muestras, el intervalo presenta 5. Para incluir el punto de inicio, fin y máximo, las muestras seleccionadas son las que se muestran en la tabla siguiente:
| Δd1 |
distancia d1 |
Perfil de Terreno |
DifDiv1 |
DifDiv2 |
DifDiv3 |
| 350 |
0 |
85 |
DifDiv11 = 0.02857 |
DifDiv12 = -6.122E-05 |
DifDiv13 = -1.123E-05 |
| 350 |
350 |
95 |
DifDiv21 = -0.01428 |
DifDiv22 = -1.127E-05 |
|
| 600 |
700 |
90 |
DifDiv31 =
-0.025 |
|
|
|
1300 |
75 |
|
|
|
Los tamaños de paso, Δd1, son diferentes, por lo que se pueden usar el método de diferencias divididas de Newton o el Método de Lagrange.
Usando diferencias divididas de Newton, se completa la tabla con las expresiones:
DifDiv_{11} = \frac{95-85}{350-0} = 0.02857143
DifDiv_{21} = \frac{90-95}{700-350} = -0.01428
DifDiv_{31} = \frac{75-90}{1300-700} =-0.025
DifDiv_{12} = \frac{-0.01428-0.02857}{700-0} = -6.122E-05
DifDiv_{22} = \frac{-0.025-(-0.01428)}{1300-350} = -1.127E-05
DifDiv_{13} = \frac{(-1.127E-05) -(6.122E-05)}{1300-0} = 1.123E-05
con lo que se puede construir el polinomio
p_{3}(d) = 85 + 0.02857(d-0)+(-6.122E5)(d-0)(d-350)+
-(1.123E-5)(d-0)(d-350)(d-700)
simplificando el polinomio se obtiene:
p_{3}(d) = 85.0+ 0.05941 d - 0.0001015 d^2 +(3.842E-8)d^3
b. Calcule el error sobre el o los datos que no se usaron en el intervalo
El valor no usado que estaba en el intervalo es d=1000, que se evalúa en p3(d) y se compara con el valor muestreado para ver el error del modelo
p_{3}(1000) = 85.0+ 0.05941 (1000) - 0.0001015 (1000)^2
+(3.842E-8)(1000)^3
p_{3}(1000) = 81.26
Error = |81.26 - 80| = 1.26
encontrando que el error es de 1.26m de altitud del terreno a los 1000m de distancia desde la referencia a la izquierda.
c. Desarrolle y justifique una propuesta para disminuir los errores encontrados en el literal anterior, sobre el mismo intervalo, es decir obtiene un nuevo polinomio (use algoritmo).
En caso de requerir una mayor precisión, se puede aumentar el grado del polinomio al incluir el punto d=1000 no usado en el paso anterior.
Usando el algoritmo con Python se obtiene:
Tabla Diferencia Dividida
[['i ', 'xi ', 'fi ', 'F[1]', 'F[2]', 'F[3]', 'F[4]', 'F[5]']]
[[ 0.0000e+00 0.0000e+00 8.5000e+01 2.8571e-02 -6.1224e-05 3.1920e-08 2.1666e-11 0.0000e+00]
[ 1.0000e+00 3.5000e+02 9.5000e+01 -1.4286e-02 -2.9304e-05 6.0086e-08 0.0000e+00 0.0000e+00]
[ 2.0000e+00 7.0000e+02 9.0000e+01 -3.3333e-02 2.7778e-05 0.0000e+00 0.0000e+00 0.0000e+00]
[ 3.0000e+00 1.0000e+03 8.0000e+01 -1.6667e-02 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00]
[ 4.0000e+00 1.3000e+03 7.5000e+01 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00]]
dDividida:
[ 2.8571e-02 -6.1224e-05 3.1920e-08 2.1666e-11 0.0000e+00]
polinomio:
2.16658863275405e-11*x*(x - 1000.0)*(x - 700.0)*(x - 350.0) + 3.19204604918891e-8*x*(x - 700.0)*(x - 350.0) - 6.12244897959184e-5*x*(x - 350.0) + 0.0285714285714286*x + 85.0
polinomio simplificado:
2.16658863275405e-11*x**4 - 1.24946064795689e-8*x**3 - 6.6683650518237e-5*x**2 + 0.0525123706702654*x + 85.0
junto a la gráfica:
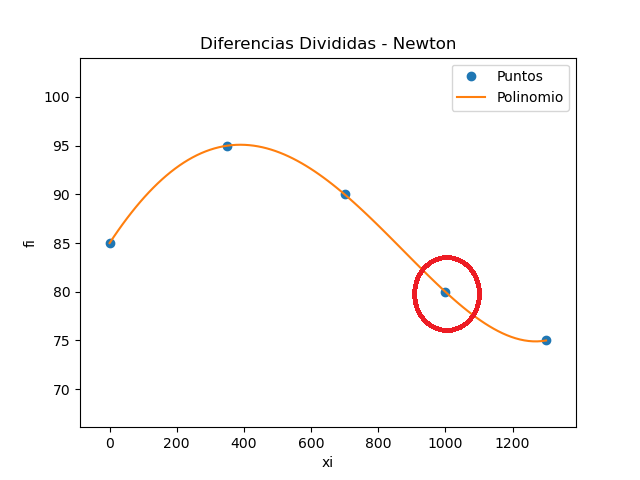
d. Escriba sus conclusiones y recomendaciones sobre los resultados obtenidos entre los dos polinomios.
Dado que el error se considera mínimo en el intervalo, y el coeficiente del polinomio para x4 es del orden de 10-11 se recomendaría usar el polinomio de grado 3.
Instrucciones en Python
# Polinomio interpolación
# Diferencias Divididas de Newton
# Tarea: Verificar tamaño de vectores,
# verificar puntos equidistantes en x
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt
# INGRESO , Datos de prueba
xi = np.array([0.0,350,700,1000,1300])
fi = np.array([85.0,95,90,80,75])
# PROCEDIMIENTO
# Tabla de Diferencias Divididas Avanzadas
titulo = ['i ','xi ','fi ']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)
# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)
# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
# Añade título para cada columna
titulo.append('F['+str(j-2)+']')
# cada fila de columna
i = 0
paso = j-2 # inicia en 1
while (i < diagonal):
denominador = (xi[i+paso]-xi[i])
numerador = tabla[i+1,j-1]-tabla[i,j-1]
tabla[i,j] = numerador/denominador
i = i+1
diagonal = diagonal - 1
j = j+1
# POLINOMIO con diferencias Divididas
# caso: puntos equidistantes en eje x
dDividida = tabla[0,3:]
n = len(dfinita)
# expresión del polinomio con Sympy
x = sym.Symbol('x')
polinomio = fi[0]
for j in range(1,n,1):
factor = dDividida[j-1]
termino = 1
for k in range(0,j,1):
termino = termino*(x-xi[k])
polinomio = polinomio + termino*factor
# simplifica multiplicando entre (x-xi)
polisimple = polinomio.expand()
# polinomio para evaluacion numérica
px = sym.lambdify(x,polisimple)
# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)
# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida')
print([titulo])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)
# Gráfica
plt.plot(xi,fi,'o', label = 'Puntos')
##for i in range(0,n,1):
## plt.axvline(xi[i],ls='--', color='yellow')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Diferencias Divididas - Newton')
plt.show()