Ejercicio: 2Eva_2021PAOI_T2 EDO para cultivo de peces
Siendo la captura una constante mas una función periódica,
h(t) = a + b \sin (2 \pi t)
La ecuación EDO del ejercicio, junto a las constantes a=0.9 y b=0.75, r=1
\frac{\delta y(t)}{\delta t} = r y(t)-h(t)
se convierte en:
\frac{\delta y(t)}{\delta t} = (1) y(t)- \Big( 0.9 + .75 \sin (2 \pi t)\Big)
\frac{\delta y(t)}{\delta t} = y(t)- 0.9 - .75 \sin (2 \pi t)
Considerando que la población inicial de peces es 1 o 100%, y(0)=1
literal a
h=1/12
tamano = muestras + 1
estimado = np.zeros(shape=(tamano,2),dtype=float)
estimado[0] = [0,1]
ti = 0
yi = 1
for i in range(1,tamano,1):
K1 = 1/12 * d1y(ti,yi)
K2 = 1/12 * d1y(ti+1/24, yi + K1/2)
K3 = 1/12 * d1y(ti+1/24, yi + K2/2)
K4 = 1/12 * d1y(ti+1/12, yi + K3)
yi = yi + (1/6)*(K1+2*K2+2*K3 +K4)
ti = ti + 1/12
estimado[i] = [ti,yi]
literal b
iteración i=0
t(0) = 0
y(0) = 1
K1 = \frac{1}{12} \Big(1- 0.9 - .75 \sin (2 \pi 0)\Big) = 0,008333
K2 = \frac{1}{12} \Big(1- 0.9 - .75 \sin \Big(2 \pi (0+\frac{1}{12})\Big)\Big) = -0.02222
y(1) = 0 + \frac{0.008333+(-0.02222)}{2} = 0.9930
t(1) = 0 + \frac{1}{12} = \frac{1}{12}
iteración i=1
t(1) = \frac{1}{12}
y(1) = 0.9930
K1 = \frac{1}{12} \Big(0.9930 - 0.9 - .75 \sin \Big( 2 \pi\frac{1}{12}\Big)\Big) = -0.02349
K2 = \frac{1}{12} \Big(0.9930 - 0.9 - .75 \sin \Big(2 \pi (\frac{1}{12}+\frac{1}{12})\Big)\Big) = -0.04832
y(1) = 0.9930 + \frac{-0.02349+(-0.04832)}{2} = 0.9571
t(1) = \frac{1}{12} + \frac{1}{12} = \frac{2}{12}
iteración i=2
t(2) = \frac{2}{12}
y(1) = 0.9571
K1 = \frac{1}{12} \Big(0.9571 - 0.9 - .75 \sin \Big( 2 \pi\frac{2}{12}\Big)\Big) = -0.04936
K2 = \frac{1}{12} \Big(0.9571 - 0.9 - .75 \sin \Big(2 \pi (\frac{2}{12}+\frac{1}{12})\Big)\Big) = -0.06185
y(1) = 0.9571 + \frac{-0.04936+(-0.06185)}{2} = 0.9015
t(3) = \frac{2}{12} + \frac{1}{12} = \frac{3}{12}
literal c
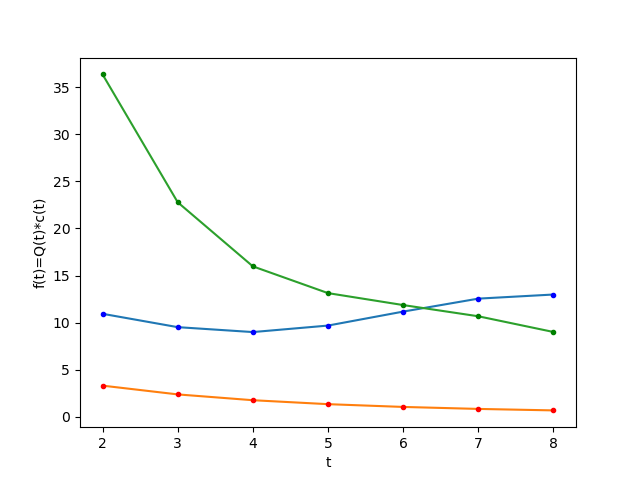
Resultado del algoritmo, muestra que la estrategia de cosecha, en el tiempo no es sostenible, dado que la población de peces en el tiempo decrece.

estimado[xi,yi,K1,K2]
[[ 0.0000e+00 1.0000e+00 8.3333e-03 -2.2222e-02]
[ 8.3333e-02 9.9306e-01 -2.3495e-02 -4.8330e-02]
[ 1.6667e-01 9.5714e-01 -4.9365e-02 -6.1852e-02]
[ 2.5000e-01 9.0153e-01 -6.2372e-02 -5.9196e-02]
[ 3.3333e-01 8.4075e-01 -5.9064e-02 -4.1109e-02]
[ 4.1667e-01 7.9066e-01 -4.0361e-02 -1.2475e-02]
[ 5.0000e-01 7.6425e-01 -1.1313e-02 1.8994e-02]
[ 5.8333e-01 7.6809e-01 2.0257e-02 4.4822e-02]
[ 6.6667e-01 8.0063e-01 4.5845e-02 5.8039e-02]
[ 7.5000e-01 8.5257e-01 5.8547e-02 5.5053e-02]
[ 8.3333e-01 9.0937e-01 5.4907e-02 3.6606e-02]
[ 9.1667e-01 9.5513e-01 3.5844e-02 7.5807e-03]
[ 1.0000e+00 9.7684e-01 6.4031e-03 -2.4313e-02]
[ 1.0833e+00 9.6788e-01 -2.5593e-02 -5.0602e-02]
[ 1.1667e+00 9.2978e-01 -5.1645e-02 -6.4322e-02]
[ 1.2500e+00 8.7180e-01 -6.4850e-02 -6.1881e-02]
[ 1.3333e+00 8.0844e-01 -6.1757e-02 -4.4027e-02]
[ 1.4167e+00 7.5554e-01 -4.3288e-02 -1.5645e-02]
[ 1.5000e+00 7.2608e-01 -1.4494e-02 1.5549e-02]
[ 1.5833e+00 7.2661e-01 1.6800e-02 4.1077e-02]
[ 1.6667e+00 7.5554e-01 4.2089e-02 5.3969e-02]
[ 1.7500e+00 8.0357e-01 5.4464e-02 5.0630e-02]
[ 1.8333e+00 8.5612e-01 5.0470e-02 3.1799e-02]
[ 1.9167e+00 8.9725e-01 3.1021e-02 2.3563e-03]
[ 2.0000e+00 9.1394e-01 1.1619e-03 -2.9991e-02]
[ 2.0833e+00 8.9953e-01 -3.1289e-02 -5.6773e-02]
[ 2.1667e+00 8.5550e-01 -5.7835e-02 -7.1028e-02]
[ 2.2500e+00 7.9107e-01 -7.1578e-02 -6.9169e-02]
[ 2.3333e+00 7.2069e-01 -6.9069e-02 -5.1948e-02]
[ 2.4167e+00 6.6018e-01 -5.1235e-02 -2.4254e-02]
[ 2.5000e+00 6.2244e-01 -2.3130e-02 6.1924e-03]
[ 2.5833e+00 6.1397e-01 7.4142e-03 3.0909e-02]
[ 2.6667e+00 6.3313e-01 3.1888e-02 4.2918e-02]
[ 2.7500e+00 6.7053e-01 4.3378e-02 3.8619e-02]
[ 2.8333e+00 7.1153e-01 3.8421e-02 1.8746e-02]
[ 2.9167e+00 7.4012e-01 1.7926e-02 -1.1830e-02]
[ 3.0000e+00 7.4317e-01 0.0000e+00 0.0000e+00]]
Instrucciones en Python
# EDO. Método de RungeKutta 2do Orden
# estima la solucion para muestras espaciadas h en eje x
# valores iniciales x0,y0
# entrega arreglo [[x,y]]
import numpy as np
def rungekutta2(d1y,x0,y0,h,muestras):
tamano = muestras + 1
estimado = np.zeros(shape=(tamano,4),dtype=float)
# incluye el punto [x0,y0]
estimado[0] = [x0,y0,0,0]
xi = x0
yi = y0
for i in range(1,tamano,1):
K1 = h * d1y(xi,yi)
K2 = h * d1y(xi+h, yi + K1)
yi = yi + (K1+K2)/2
xi = xi + h
estimado[i-1,2:]=[K1,K2]
estimado[i] = [xi,yi,0,0]
return(estimado)
# PROGRAMA PRUEBA
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1
# INGRESO
# d1y = y' = f, d2y = y'' = f'
a =0.9; b=0.75; r=1
d1y = lambda t,y: r*y-(a+b*np.sin(2*np.pi*t))
x0 = 0
y0 = 1
h = 1/12
muestras = 12*3
# PROCEDIMIENTO
puntosRK2 = rungekutta2(d1y,x0,y0,h,muestras)
xi = puntosRK2[:,0]
yiRK2 = puntosRK2[:,1]
# SALIDA
np.set_printoptions(precision=4)
print('estimado[xi,yi,K1,K2]')
print(puntosRK2)
# Gráfica
import matplotlib.pyplot as plt
plt.plot(xi[0],yiRK2[0],
'o',color='r', label ='[x0,y0]')
plt.plot(xi[1:],yiRK2[1:],
'o',color='m',
label ='y Runge-Kutta 2 Orden')
plt.title('EDO: Solución con Runge-Kutta 2do Orden')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()