Ejercicio: 1Eva_IIT2018_T2 Distancia mínima a un punto
Literal a
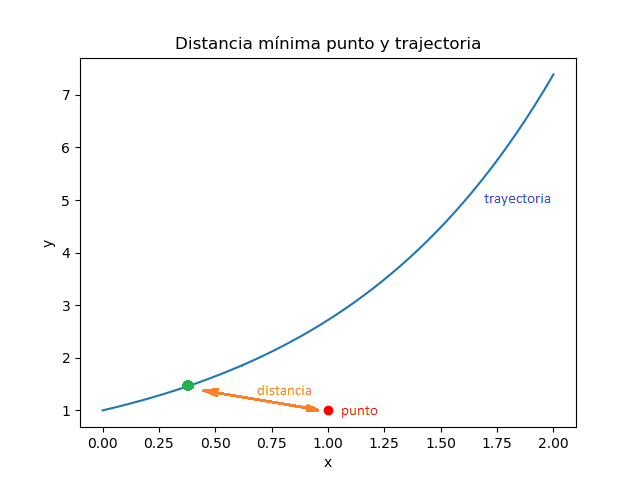
Se requiere analizar la distancias entre una trayectoria y el punto = [1,1]
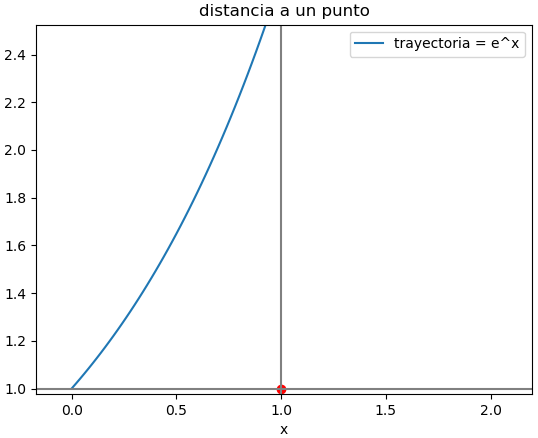
Al analizar las distancias de ex y el punto [1,1] se trazan lineas paralelas a los ejes desde el punto [1,1], por lo que se determina que el intervalo de x = [a,b] para distancias se encuentra en:
a > 0, a = 0.1
b < 1, b = 0.7
El ejercicio usa la fórmula de distancia entre dos puntos:
d = \sqrt{(x_2-x_1)^2+(y_2- y_1)^2}
en los cuales:
[x1,y1] = [1,1]
[x2,y2] = [x, ex]
que al sustituir en la fórmula se convierte en:
d = \sqrt{(x-1)^2+(e^x- 1)^2}
que es lo requerido en el literal a
Literal b
Para usar un método de búsqueda de raíces, se requiere encontrar el valor cuando f(x) = d' = 0.
Un método como el de Newton Raphson requiere también f'(x) = d''
f(x) = \frac{x + (e^x - 1)e^x - 1}{\sqrt{(x - 1)^2 + (e^x - 1)^2}}
f'(x)= \frac{(e^x - 1)e^x + e^{2x} + 1 - \frac{(x + (e^x - 1)e^x - 1)^2}{(x - 1)^2 + (e^x - 1)^2}} {\sqrt{(x - 1)^2 + (e^x - 1)^2}}
expresiones obtenidas usando Sympy
f(x) :
(x + (exp(x) - 1)*exp(x) - 1)/sqrt((x - 1)**2 + (exp(x) - 1)**2)
f'(x) :
((exp(x) - 1)*exp(x) + exp(2*x) + 1 - (x + (exp(x) - 1)*exp(x) - 1)**2/((x - 1)**2 + (exp(x) - 1)**2))/sqrt((x - 1)**2 + (exp(x) - 1)**2)
f(x) :
/ x \ x
x + \e - 1/*e - 1
--------------------------
______________________
/ 2
/ 2 / x \
\/ (x - 1) + \e - 1/
f'(x) :
2
/ / x \ x \
/ x \ x 2*x \x + \e - 1/*e - 1/
\e - 1/*e + e + 1 - ----------------------
2
2 / x \
(x - 1) + \e - 1/
-----------------------------------------------
______________________
/ 2
/ 2 / x \
\/ (x - 1) + \e - 1/
lo que permite observar la raíz de f(x) en una gráfica:
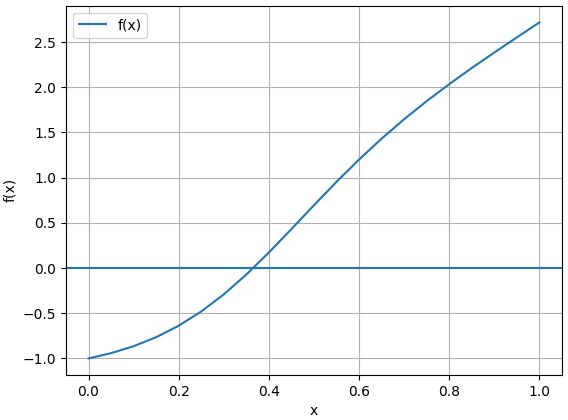
con las siguientes instrucciones:
# Eva_IIT2018_T2 Distancia mínima a un punto
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
# INGRESO
x = sym.Symbol('x')
fx = sym.sqrt((x-1)**2+(sym.exp(x) -1)**2)
a = 0
b = 1
muestras = 21
# PROCEDIMIENTO
dfx = sym.diff(fx,x,1)
d2fx = sym.diff(fx,x,2)
f = sym.lambdify(x,dfx)
xi = np.linspace(a,b,muestras)
fi = f(xi)
# SALIDA
print('f(x) :')
print(dfx)
print("f'(x) :")
print(d2fx)
print()
print('f(x) :')
sym.pprint(dfx)
print("f'(x) :")
sym.pprint(d2fx)
# GRAFICA
plt.plot(xi,fi, label='f(x)')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid()
plt.show()
Usando el método de la bisección para el intervalo dado, se tiene:
f(x) = \frac{x + (e^x - 1)e^x - 1}{\sqrt{(x - 1)^2 + (e^x - 1)^2}}
itera = 0 , a = 0, b=1
c= \frac{0+1}{2} = 0.5
f(0) = \frac{0 + (e^0 - 1)e^0 - 1}{\sqrt{(0 - 1)^2 + (e^0 - 1)^2}} = -1
f(1) = \frac{1 + (e^1 - 1)e^1 - 1}{\sqrt{(1 - 1)^2 + (e^1 - 1)^2}} 2.7183
f(0.5) = \frac{(0.5) + (e^(0.5) - 1)e^(0.5) - 1}{\sqrt{((0.5) - 1)^2 + (e^(0.5) - 1)^2}} = 0.6954
cambio de signo a la izquierda,
a= 0, b=c=0.5
tramo = |0.5-0| = 0.5
itera = 1
c= \frac{0+0.5}{2} = 0.25
f(0.25) = \frac{(0.25) + (e^(0.25) - 1)e^(0.25) - 1}{\sqrt{((0.25) - 1)^2 + (e^(0.25) - 1)^2}} = -0.4804
cambio de signo a la derecha,
a=c= 0.25, b=0.5
itera = 2
c= \frac{0.25+0.5}{2} = 0.375
f(0.375) = \frac{(0.375) + (e^(0.375) - 1)e^(0.375) - 1}{\sqrt{((0.375) - 1)^2 + (e^(0.375) - 1)^2}} = 0.0479
cambio de signo a la izquierda,
a= 0.25, b=c=0.375
se continúan las iteraciones con el algoritmo, para encontrar la raíz en 0.364:
método de Bisección
i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
tramo
0 [0, 0.5, 1] [-1. 0.6954 2.7183]
0.5
1 [0, 0.25, 0.5] [-1. -0.4804 0.6954]
0.25
2 [0.25, 0.375, 0.5] [-0.4804 0.0479 0.6954]
0.125
3 [0.25, 0.3125, 0.375] [-0.4804 -0.2388 0.0479]
0.0625
4 [0.3125, 0.34375, 0.375] [-0.2388 -0.1004 0.0479]
0.03125
5 [0.34375, 0.359375, 0.375] [-0.1004 -0.0274 0.0479]
0.015625
6 [0.359375, 0.3671875, 0.375] [-0.0274 0.01 0.0479]
0.0078125
7 [0.359375, 0.36328125, 0.3671875] [-0.0274 -0.0088 0.01 ]
0.00390625
8 [0.36328125, 0.365234375, 0.3671875] [-0.0088 0.0006 0.01 ]
0.001953125
9 [0.36328125, 0.3642578125, 0.365234375] [-0.0088 -0.0041 0.0006]
0.0009765625
raíz en: 0.3642578125
Al algoritmo anterior se complementa con las instrucciones de la función para la bisección.
# Eva_IIT2018_T2 Distancia mínima a un punto
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
# INGRESO
x = sym.Symbol('x')
fx = sym.sqrt((x-1)**2+(sym.exp(x) -1)**2)
a = 0
b = 1
muestras = 21
# PROCEDIMIENTO
dfx = sym.diff(fx,x,1)
d2fx = sym.diff(fx,x,2)
f = sym.lambdify(x,dfx)
xi = np.linspace(a,b,muestras)
fi = f(xi)
# SALIDA
print('f(x) :')
print(dfx)
print("f'(x) :")
print(d2fx)
print()
print('f(x) :')
sym.pprint(dfx)
print("f'(x) :")
sym.pprint(d2fx)
# GRAFICA
plt.plot(xi,fi, label='f(x)')
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid()
plt.show()
# Algoritmo de Bisección
# [a,b] se escogen de la gráfica de la función
# error = tolera
import numpy as np
def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4):
'''
Algoritmo de Bisección
Los valores de [a,b] son seleccionados
desde la gráfica de la función
error = tolera
'''
fa = fx(a)
fb = fx(b)
tramo = np.abs(b-a)
itera = 0
cambia = np.sign(fa)*np.sign(fb)
if cambia<0: # existe cambio de signo f(a) vs f(b)
if vertabla==True:
print('método de Bisección')
print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
print(' ','tramo')
np.set_printoptions(precision)
while (tramo>=tolera and itera<=iteramax):
c = (a+b)/2
fc = fx(c)
cambia = np.sign(fa)*np.sign(fc)
if vertabla==True:
print(itera,[a,c,b],np.array([fa,fc,fb]))
if (cambia<0):
b = c
fb = fc
else:
a = c
fa = fc
tramo = np.abs(b-a)
if vertabla==True:
print(' ',tramo)
itera = itera + 1
respuesta = c
# Valida respuesta
if (itera>=iteramax):
respuesta = np.nan
else:
print(' No existe cambio de signo entre f(a) y f(b)')
print(' f(a) =',fa,', f(b) =',fb)
respuesta=np.nan
return(respuesta)
# INGRESO
tolera = 0.001
# PROCEDIMIENTO
respuesta = biseccion(f,a,b,tolera,vertabla=True)
# SALIDA
print('raíz en: ', respuesta)
.