Ejercicio: 3Eva_2024PAOII_T2 Interpolar trayectoria helicóptero

xi = [0.  , 2.50, 3.75, 5.00, 6.25, 7.5 ]
yi = [3.7 , 3.25, 4.05, 4.33, 2.95, 3.22]

literal a

Según la gráfica presentada, los puntos a considerar para todo el intervalo, deberían ser al menos el primero y el último. Para un polinomio de grado 3 se requieren usar 4 muestras, por lo que faltarían dos muestras dentro del intervalo. Los puntos adicionales estarían entre los puntos intermedios, tratando de mantener una distancia equidistante entre ellos y tratar de mantener los cambios de dirección.

Los puntos seleccionados para el ejercicio serán

xi = [0. , 2.50, 5.00, 7.5 ]
fi = [3.7 , 3.25, 4.33, 3.22]

Se puede construir el polinomio con los cualquiera de los métodos para interpolación dado que tienen tamaños de paso iguales entre tramos.

Desarrollando con el método de Lagrange, el polinomio se construye como:

término 1

L_{0} (x) = \frac{(x-2.5)(x-5.0)(x-7.5)}{(0-2.5)(0-5.0)(0-7.5)}

término 2

L_{1} (x) = \frac{(x-0)(x-5.0)(x-7.5)}{(2.5-0)(2.5-5.0)(2.5-7.5)}

término 3

L_{2} (x) = \frac{(x-0)(x-2.5)(x-7.5)}{(5-0)(5-2.5)(5-7.5)}

término 4

L_{3} (x) = \frac{(x-0)(x-2.5)(x-5)}{(7.5-0)(7.5-2.5)(7.5-5)}

se construye el polinomio usando la fórmula para f_n(x) para cada valor fi,

p_3(x) = 3.7 \frac{(x-2.5)(x-5.0)(x-7.5)}{(0-2.5)(0-5.0)(0-7.5)} + 3.25 \frac{(x-0)(x-5.0)(x-7.5)}{(2.5-0)(2.5-5.0)(2.5-7.5)} + 4.33 \frac{(x-0)(x-2.5)(x-7.5)}{(5-0)(5-2.5)(5-7.5)} + 3.22 \frac{(x-0)(x-2.5)(x-5)}{(7.5-0)(7.5-2.5)(7.5-5)}

simplificando con Sympy:

Polinomio de Lagrange, expresiones
0.104*x*(x - 7.5)*(x - 5.0) - 0.13856*x*(x - 7.5)*(x - 2.5) + 0.0343466666666667*x*(x - 5.0)*(x - 2.5) - 0.0394666666666667*(x - 7.5)*(x - 5.0)*(x - 2.5)

Polinomio de Lagrange: 
-0.03968*x**3 + 0.42*x**2 - 0.982*x + 3.7

p_3(x) = 3.7 - 0.982x + 0.42 x^2 -0.03968 x^3

literal b

Para verificar que el polinomio pasa por los puntos, se puede usar una gráfica o al menos dos puntos usados para crear el polinomio:

p_3(2.5) = 3.7 - 0.982(2.5) + 0.42 (2.5)^2 -0.03968 (2.5)^3 = 3.25 p_3(5) = 3.7 - 0.982(5) + 0.42 (5)^2 -0.03968 (5)^3 = 4.33

>>> polisimple
-0.03968*x**3 + 0.42*x**2 - 0.982*x + 3.7
>>> polisimple.subs(x,2.5)
3.25000000000000
>>> polisimple.subs(x,5)
4.33000000000000
>>>

Se comprueba que los valores obtenidos corresponden a las muestras, por lo que el polinomio cumple con los criterios básicos de interpolación. La gráfica permite verificar también el resultado.

literal c

Error en puntos no usados de las muestras

p_3(3.75) = 3.7 - 0.982(3.75) + 0.42 (3.75)^2 -0.03968 (3.75)^3 = 3.83125

error = |3.83125 - 4.05| = 0.218

p_3(6.25) = 3.7 - 0.982(6.25) + 0.42 (6.25)^2 -0.03968 (6.25)^3 = 4.28125

error = |4.28125 - 4.05| = 1.3312

literal d

Observando las gráficas de la trayectoria construida junto a las funciones descritas en el tema 1 se tiene que:

Un polinomio de grado 3 es insuficiente para describir la trayectoria, se debe aumentar el grado del polinomio para ajustar mejor la curva.

Por ejemplo, usando todos los puntos, la trayectoria y el polinomio son mas cercanas aunque no iguales.

literal e

Encontrar el error en P(5), como x=5 y es parte de los puntos de muestra, el error debería ser cero. Siempre y cuando x=5 sea parte de los puntos seleccionados.

p_3(5) = 3.7 - 0.982(5) + 0.42 (5)^2 -0.03968 (5)^3 = 4.33

error = | 4.33-4.33| = 0

literal f

Los resultados con el algoritmo de Lagrange se muestran como:

    valores de fi:  [3.7  3.25 4.33 3.22]
divisores en L(i):  [-93.75  31.25 -31.25  93.75]

Polinomio de Lagrange, expresiones
0.104*x*(x - 7.5)*(x - 5.0) - 0.13856*x*(x - 7.5)*(x - 2.5) + 0.0343466666666667*x*(x - 5.0)*(x - 2.5) - 0.0394666666666667*(x - 7.5)*(x - 5.0)*(x - 2.5)

Polinomio de Lagrange: 
-0.03968*x**3 + 0.42*x**2 - 0.982*x + 3.7

Algoritmo en Python. Interpolación polinómica de Lagrange

# 3Eva_2024PAOII_T2 Interpolar trayectoria helicóptero
# Interpolacion de Lagrange
# divisoresL solo para mostrar valores
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO , Datos de prueba
# todos los datos
xj = [0.  , 2.50, 3.75, 5.00, 6.25, 7.5 ]
fj = [3.7 , 3.25, 4.05, 4.33, 2.95, 3.22]

# datos seleccionados
xi = [0.  , 2.50, 5.00, 7.5 ]
fi = [3.7 , 3.25, 4.33, 3.22]

# trayectoria
gx = lambda t: 0.5*t +0 *t
gy = lambda t: np.sin(0.10*t)*np.cos(0.7*t)+ 3.7

ta = 0 ; tb = 15
muestrast = 7
muestrasj = 4*muestrast

# PROCEDIMIENTO
# trayectoria
tj = np.linspace(ta,tb,muestrasj)
gxj = gx(tj)
gyj = gy(tj)

# Interpolación
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
    
    # Termino de Lagrange
    numerador = 1
    denominador = 1
    for j  in range(0,n,1):
        if (j!=i):
            numerador = numerador*(x-xi[j])
            denominador = denominador*(xi[i]-xi[j])
    terminoLi = numerador/denominador

    polinomio = polinomio + terminoLi*fi[i]
    divisorL[i] = denominador

# simplifica el polinomio
polisimple = polinomio.expand()

# para evaluación numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
print('    valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)

# Gráfica
plt.plot(gxj,gyj,color='orange', label = 'trayectoria')
plt.plot(xi,fi,'o', label = 'muestras')
plt.plot(pxi,pfi,color='green',linestyle='dashed', label = 'P(x)')
plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.grid()
plt.title('Interpolación Lagrange')
plt.show()

Ejercicio: 3Eva_2024PAOII_T1 Accidente entre aeronaves

literal a

La distancia entre las aeronaves se determina a partir de las ecuaciones proporcionadas en el enunciado.

d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}

La ecuación también mantiene la forma y el mínimo si se utiliza el cuadrado de la distancia:

D = d^2 = (x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2

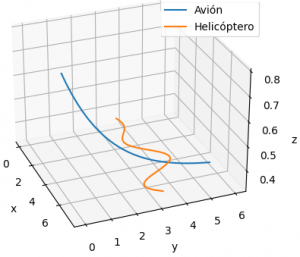
Las diferencias de distancia por eje pueden ser convergentes hacia el punto de impacto, dado que se conoce que el accidente ya ocurrió. Por lo que también se pueden revisar las distancias entre ejes en lugar de la distancia total en 3D, simplificando un poco el ejercicio. Observe la gráfica proporcionada:

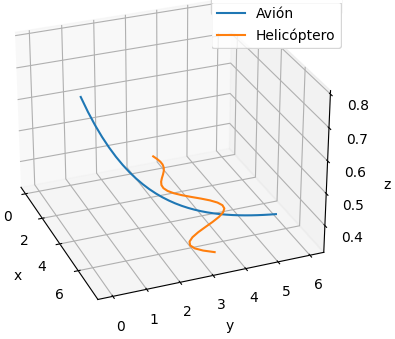
Avión	Helicóptero	distancia por eje
Ax(t) = 5.1	Hx(t) = 0.5t	|0.5t-5.1|
Ay(t) = 0.4t	Hy(t) = sin(0.1t)cos(0.7t)+3.7	|sin(0.1t)cos(0.7t) + 3.7-0.4|
Az(t) = 0.5 e^{-0.2t} + 0.3	Hz(t) = 0.36	|0.36 - (0.5 e^{-0.2t} + 0.3)|

D = (0.5t-5.1)^2 + (sin(0.1t)cos(0.7t)+3.7-0.4t)^2 + (0.36-(0.5 e^{-0.2t} + 0.3))^2 dx =0.5t-5.1 dy = sin(0.1t)cos(0.7t) + 3.7-0.4 dz = 0.36 - (0.5 e^{-0.2t} + 0.3)

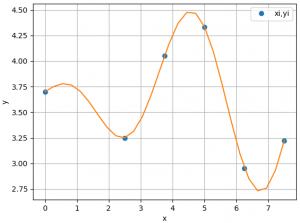
Se realiza la gráfica para la distancia al cuadrado Di y las distancias por cada eje dxi, dyi, dzi :

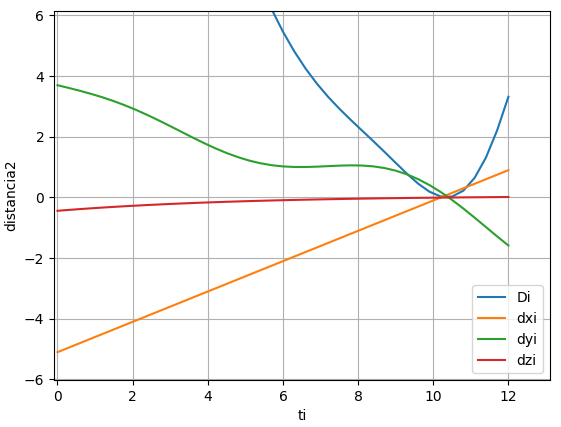
Por lo que el resultado también se podría determinar usando por ejemplo el eje y. La ecuación a buscar la distancia mínima, punto de choque o cruce por cero podría ser:

f(t) =dy(t)= sin(0.1t)cos(0.7t) + 3.7-0.4t = 0

literal b

Por la gráfica se puede obtener un intervalo de búsqueda entre [8, 12], que usando solo las distancias en el eje y, se tiene:

dy(8) =1.0563 dy(12) =-1.5839

literal c

Se pide usar un método de búsqueda de raíces, pudiendo seleccionar Bisección en el intervalo encontrado en el literal b.

iteración 1

a = 8, b=12 c = \frac{a+b}{2} = \frac{8+12}{2} = 10 f(8) = 1.0563 f(10) =sin(0.1(10))cos(0.7(10)) + 3.7-0.4(10) = 0.3343 f(12) = -1.5839

cambio de signo a la derecha

a = 10, b = 12 tramo = |12-10| =2

iteración 2

a = 10, b=12 c = \frac{10+12}{2} = 11 f(11) =sin(0.1(11))cos(0.7(11)) + 3.7-0.4(11) = -0.5633

cambio de signo a la izquierda

a = 10, b = 11 tramo = |11-10| = 1

iteración 3

a = 10, b=11 c = \frac{10+11}{2} = 10.5 f(10.5) =sin(0.1(10.5))cos(0.7(10.5)) + 3.7-0.4(10.5) = -0.0811

cambio de signo a la izquierda

a = 10, b = 10.5 tramo = |10.5-10| = 0.5

literal d

La variable independiente en el ejercicio es tiempo 't', que podría ser segundos. Si la tolerancia se estima en milisegundos, tolera = 10-3 .

El error se ha calculado en cada iteración

literal e

El error disminuye en cada iteración, por lo que el método converge.

La distancia mínima entre las aeronaves no tiene que llegar a cero para que se produzca un accidente. Las dimensiones de las aeronaves muestran que se encuentran entre 70m y 4 m, por lo que se estima que debe existir una separación mayor a 70 metros en cualquiera de los ejes para evitar un accidente. Si las coordenadas se estiman en Km, la tolerancia sería de 0.070 Km al considerar más de 70 metros como la distancia segura.

literal f

Usando el algoritmo se encuentra la raíz en:

i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)']
   tramo
0 [8, 10.0, 12] [ 1.0564  0.3344 -1.584 ]
   2.0
1 [10.0, 11.0, 12] [ 0.3344 -0.5633 -1.584 ]
   1.0
2 [10.0, 10.5, 11.0] [ 0.3344 -0.0811 -0.5633]
   0.5
3 [10.0, 10.25, 10.5] [ 0.3344  0.1368 -0.0811]
   0.25
4 [10.25, 10.375, 10.5] [ 0.1368  0.0302 -0.0811]
   0.125
5 [10.375, 10.4375, 10.5] [ 0.0302 -0.0249 -0.0811]
   0.0625
6 [10.375, 10.40625, 10.4375] [ 0.0302  0.0028 -0.0249]
   0.03125
7 [10.40625, 10.421875, 10.4375] [ 0.0028 -0.011  -0.0249]
   0.015625
8 [10.40625, 10.4140625, 10.421875] [ 0.0028 -0.0041 -0.011 ]
   0.0078125
9 [10.40625, 10.41015625, 10.4140625] [ 0.0028 -0.0007 -0.0041]
   0.00390625
10 [10.40625, 10.408203125, 10.41015625] [ 0.0028  0.001  -0.0007]
   0.001953125
11 [10.408203125, 10.4091796875, 10.41015625] [ 0.001   0.0002 -0.0007]
   0.0009765625
raíz en:  10.4091796875

Por lo que las coordenadas de choque entre aeronaves será:

Avión	Helicóptero	distancia por eje
Ax(t) = 5.1	Hx(t) = 0.5 (10.40) = 5.2	|5.1-5.2| = 0.1
Ay(t) = 0.4(10.4) = 4.16	Hy(t) = sin(0.1(10.40))cos(0.7(10.40))+3.7 = 4.168	|4.16 - 4.168| = 0.008
Az(10.4) = 0.5 e^{-0.2(10.4)} + 0.3 = 0.3624	Hz(t) = 0.36	|0.3624 - 0.36|  = 0.0024

Instrucciones en Python para Gráfica de distancias

import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO
# Avión Aterriza
Ax = lambda t: 5.1 + 0*t
Ay = lambda t: 0.4*t
Az = lambda t: 0.5*np.exp(-0.2*t) + 0.3
# helicóptero
Hx = lambda t: 0.5*t + 0*t
Hy = lambda t: np.sin(0.10*t)*np.cos(0.7*t)+ 3.7
Hz = lambda t: 0.36 + 0*t

a = 0
b = 6/0.5 # x entre[0,6] usando gx(t)= 6
muestras = 41

# PROCEDIMIENTO
# Distancia por ejes
dx = lambda t: Hx(t) - Ax(t)
dy = lambda t: Hy(t) - Ay(t)
dz = lambda t: Hz(t) - Az(t)
# Distancia 3D
distancia2 = lambda t: dx(t)**2 + dy(t)**2 + dz(t)**2

# Simulacion en segmento t=[a,b]
ti = np.linspace(a,b,muestras)
dxi = dx(ti)
dyi = dy(ti)
dzi = dz(ti)

Di = distancia2(ti)

# SALIDA
print(dy(8))
print(dy(12))

plt.plot(ti,Di, label='Di')
plt.plot(ti,dxi,label='dxi')
plt.plot(ti,dyi,label='dyi')
plt.plot(ti,dzi,label='dzi')
plt.xlabel('ti')
plt.ylabel('distancia2')
plt.grid()
plt.legend()
plt.show()

Instrucciones en Python - Algoritmo Bisección

# 3Eva_2024PAOII_T1 Accidente entre aeronaves
# Algoritmo de Bisección
# [a,b] se escogen de la gráfica de la función
# error = tolera

import numpy as np
import matplotlib.pyplot as plt

# Algoritmo de Bisección
# [a,b] se escogen de la gráfica de la función
# error = tolera
import numpy as np

def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4):
    '''
    Algoritmo de Bisección
    Los valores de [a,b] son seleccionados
    desde la gráfica de la función
    error = tolera
    '''
    fa = fx(a)
    fb = fx(b)
    tramo = np.abs(b-a)
    itera = 0
    cambia = np.sign(fa)*np.sign(fb)
    if cambia<0: # existe cambio de signo f(a) vs f(b)
        if vertabla==True:
            print('método de Bisección')
            print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)'])
            print('  ','tramo')
            np.set_printoptions(precision)
            
        while (tramo>=tolera and itera<=iteramax):
            c = (a+b)/2
            fc = fx(c)
            cambia = np.sign(fa)*np.sign(fc)
            if vertabla==True:
                print(itera,[a,c,b],np.array([fa,fc,fb]))
            if (cambia<0):
                b = c
                fb = fc
            else:
                a = c
                fa = fc
            tramo = np.abs(b-a)
            if vertabla==True:
                print('  ',tramo)
            itera = itera + 1
        respuesta = c
        # Valida respuesta
        if (itera>=iteramax):
            respuesta = np.nan

    else: 
        print(' No existe cambio de signo entre f(a) y f(b)')
        print(' f(a) =',fa,',  f(b) =',fb) 
        respuesta=np.nan
    return(respuesta)

# INGRESO
fx = lambda t: np.sin(0.10*t)*np.cos(0.7*t)+ 3.7 - 0.4*t 
a = 8
b = 12
tolera = 0.001

# PROCEDIMIENTO
respuesta = biseccion(fx,a,b,tolera,vertabla=True)
# SALIDA
print('raíz en: ', respuesta)

Ejercicio: 2Eva_2024PAOII_T2 EDO Mayoría entre grupos Azules y Rojos

literal a

La población anual del país se describe con x(t), con tasas de natalidad a = 0.018 y mortalidad b = 0.012,

f(t,x,,y) = \frac{\delta x}{\delta t} = 0.018 x - 0.012 x^2

La población de Rojos es minoría y se describe con y(t). Los valore iniciales son: x(0)=2 , y(0)=0.5 y tamaño de paso h=0.5

g(t,x,y) = \frac{\delta y}{\delta t} = 0.026x - 0.017 y^2 +0.19 (0.012) (x-y)

el algoritmo de Runge-Kutta para sistemas de ecuaciones aplicado al ejercicio:

K1x = h f(t,x,y) = h (0.018 x - 0.012 x^2) K1y = h g(t,x,y) = h \Big(0.026x - 0.017 y^2 +0.19 (0.012) (x-y)\Big) K2x = h f(t+h,x+K1x,y+K1y) = h (0.018 (x+K1x) - 0.012 (x+K1x)^2) K2y = h g(t+h,x+K1x,y+K1y) = h \Big(0.026(x+K1x) - 0.017 (y + K1y)^2 +0.19 (0.012) ((x+K1x)-(y + K1y))\Big) x[i+1] = x[i] + \frac{K1x+K2x}{2} y[i+1] = y[i] + \frac{K1y+K2y}{2} t[i+1] = t[i] + h

literal b

Desarrolle tres iteraciones con expresiones completas para x(t), y(t) con tamaño de paso h=0.5.

itera = 0

K1x = 0.5 (0.018 (2) - 0.012 (2)^2) = -0.006 K1y = 0.5 \Big(0.026(2) - 0.017 (0.5)^2 +0.19 (0.012) ((2)-(0.5))\Big) = 0.006085 K2x = 0.5 (0.018 (2-0.006) - 0.012 (2-0.006)^2) = -0.00591 K2y = 0.5 \Big(0.026(2-0.006) - 0.017 (0.5 + 0.006085)^2 +0.19 (0.012) ((2-0.006)-(0.5 + 0.006085))\Big) = 0.006098 x[1] = 2 + \frac{-0.006+-0.00591}{2} = 1.9940 y[1] = 0.5 + \frac{0.006085+0.006098}{2} = 0.5060 t[1] = 0 + 0.5 =0.5

itera = 1

K1x = 0.5 (0.018 (1.9940) - 0.012 (1.9940)^2) =-0.005911 K1y = 0.5 \Big(0.0261.9940 - 0.017 (0.5060)^2 +0.19 (0.012) (1.9940-y)\Big) = 0.006098 K2x = 0.5 (0.018 (1.9940-0.005911) - 0.012 (1.9940-0.005911)^2 = -0.005823 K2y = 0.5 \Big(0.026(1.9940-0.005911) - 0.017 (0.5060 + 0.006098)^2 +0.19 (0.012) ((1.9940-0.005911)-(0.5060 + 0.006098))\Big) = 0.006111 x[2] = 1.9940 + \frac{-0.005911-0.005823}{2} = 1.988178 y[2] = 0.5060 + \frac{0.006098+0.006111}{2} = 0.512196 t[2] = 0.5 + 0.5 = 1

itera = 2

K1x = 0.5 (0.018 (1.988178) - 0.012 (1.988178)^2) =-0.005824 K1y = 0.5 \Big(0.026(0.512196) - 0.017 (0.512196)^2 +0.19 (0.012) (1.988178-0.512196)\Big) = 0.006111 K2x = 0.5 (0.018 (1.988178-0.005824) - 0.012 (1.988178-0.005824)^2) =-0.005737 K2y = 0.5 \Big(0.026(0.512196+0.006111) - 0.017 (0.512196 + 0.006111 )^2 +0.19 (0.012) ((1.988178-0.005911)-(0.512196 + 0.006111)\Big) =0.006124 x[3] = (1.988178) + \frac{-0.005824-0.005737}{2} = 1.982398 y[3] = 0.512196 + \frac{0.006111+0.006124}{2} = 0.518314 t[3] = 1 + 0.5 = 1.5

literal c

Los resultados para x(t) de las primeras iteraciones indican que la población total del país disminuye en el intervalo observado. Se puede comprobar al usar el algoritmo para mas iteraciones como se muestra en la gráfica.

literal d

Los resultados para y(t) muestran que la población clasificada como Rojo aumenta en el intervalo observado. Sin embargo la mayoría sigue siendo Azul para las tres iteraciones realizadas.

literal e

La población y(t) alcanza la mitad de la población cuanto t cambia de 30.5 a 31. Tiempo en el que de realizar elecciones, ganarían los Rojos.

Usando el algoritmo, se añade una columna con la condición que MayoriaY = yi>xi/2, que se convierte a 1 o verdadero cuando se cumple la condición. Con lo que se encuentra el cambio de mayoría a Rojo.

Runge-Kutta Segundo Orden
i  [ ti,  xi,  yi ]
   [ K1x,  K1y,  K2x,  K2y , MayoriaY]
0 [0.  2.  0.5]
   [0. 0. 0. 0. 0.]
1 [0.5      1.994045 0.506092]
  [-0.006     0.006085 -0.00591   0.006098  0.      ]
2 [1.       1.988178 0.512196]
  [-0.005911  0.006098 -0.005823  0.006111  0.      ]
3 [1.5      1.982398 0.518314]
  [-0.005824  0.006111 -0.005737  0.006124  0.      ]
4 [2.       1.976702 0.524443]
…
   [-0.002761  0.005927 -0.002727  0.005907  0.      ]
60 [30.        1.755801  0.869617]
   [-0.002728  0.005907 -0.002695  0.005887  0.      ]
61 [30.5       1.753123  0.875494]
   [-0.002695  0.005887 -0.002662  0.005867  0.      ]
62 [31.        1.750476  0.88135 ]
   [-0.002663  0.005867 -0.002631  0.005846  1.      ]
63 [31.5       1.747861  0.887185]
   [-0.002631  0.005846 -0.002599  0.005824  1.      ]
64 [32.        1.745277  0.892998]
   [-0.002599  0.005824 -0.002568  0.005802  1.      ]
65 [32.5       1.742724  0.898789]
   [-0.002568  0.005802 -0.002538  0.00578   1.      ]
66 [33.        1.740201  0.904558]
   [-0.002538  0.00578  -0.002508  0.005757  1.      ]
67 [33.5       1.737708  0.910303]
   [-0.002508  0.005757 -0.002478  0.005734  1.      ]

 

Ejercicio: 2Eva_2024PAOII_T1 Área de incendio forestal en Cerro Azul

literal a

Calcular los tamaños de paso dxi en cada frontera y plantear la integración con fórmulas compuestas.

Usando los datos de las coordenadas de obtiene cada dxi = xi[i+1]-xi[i]. De forma semejante se encuentra cada dxj, Seleccionando los métodos según se disponga de tamaño de paso iguales y consecutivos como se muestra en la tabla ampliada.

Frontera superior

		Trapecio		Trapecio			Trapecio		Trapecio			Simpson 1/3
	Trapecio		Trapecio		Simpson 1/3			Trapecio		Simpson 1/3
dxi	40	100	-30	66	20	20	79	125	54	50	50	20	20	--
xi	410	450	550	520	586	606	626	705	830	884	934	984	1004	1024
yi	131	194	266	337	402	483	531	535	504	466	408	368	324	288

Frontera Inferior

				Trapecio
	Simpson 3/8
dxj	190	190	190	44	--
xj	410	600	790	980	1024
yj	131	124	143	231	288

Desarrollando con instrucciones sobre el arreglo en Python con la instrucción np.diff(xi).

>>> xi = [410, 450, 550, 520, 586, 606, 626, 705, 830,
          884, 934, 984, 1004, 1024]
>>> xi = np.array(xi)
>>> dxi = np.diff(xi)
>>> dxi
array([ 40, 100, -30, 66, 20, 20, 79, 125, 54,
        50, 50, 20, 20])
>>> xj = [410, 600, 790, 980, 1024]
>>> dxj = np.array(xj)
>>> dxj = np.diff(xj)
>>> dxj
array([190, 190, 190, 44])
>>>

literal b

Desarrollar las expresiones del área para las coordenadas de la frontera superior, según el literal a. Cuando se tienen dos tamaños de paso iguales se usa Simpson de 1/3.

I_{superior} = 40\Big(\frac{131+194}{2}\Big) +100\Big(\frac{194+266}{2}\Big) + -30\Big(\frac{266+337}{2}\Big) +66\Big(\frac{337+402}{2}\Big)+ + \frac{20}{3}\Big(402+4(483)+531\Big) + +79\Big(\frac{531+535}{2}\Big) +125\Big(\frac{535+504}{2}\Big) + 54\Big(\frac{504+466}{2}\Big) + + \frac{50}{3}\Big(466+4(408)+368\Big) + + \frac{20}{3}\Big(368+4(324)+288\Big) I_{superior} = 254753,33

literal c

Realice los cálculos para la frontera inferior y encuentre el área afectada. Con tres tamaños de paso iguales se usa Simpson de 3/8.

I_{Inferior} = \frac{3}{8}(190)\Big(131+3(124)+3(143)+231\Big) +44\Big(\frac{231+288}{2}\Big) = 94281,75

Área total afectada:

A_{afectada} = I_{superior} - I_{Inferior} = 254753,33 -94281,75 A_{afectada} = 160.471,58

literal d

Estime la cota de error en los cálculos.

Considere usar las unidades en Km en lugar de metros para los tamaños de paso.

Error_{truncaSup} = O( 0.040^3) + O(0. 100^3)+ O( (-0.030)^3) + O( 0.066^3)+ + O( 0.020^5) + O(0. 079^3)+ O( 0.125^3) + O( 0.054^3)+ + O( 0.050^5) + O( 0.020^5) Error_{truncaInf} = O( 0.190^5) + O(0. 044^3)