Categoría: 2da Evaluación

2Eva_2023PAOII_T2 EDO Cable cuelga entre apoyos A y B

2ra Evaluación 2023-2024 PAO II. 30/Enero/2024

Tema 2 (40 puntos) Un cable cuelga de dos apoyos en A y B.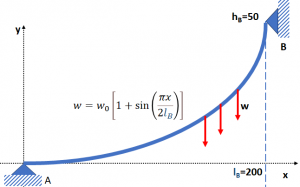

El cable sostiene una carga distribuida cuya magnitud varía con x según la ecuación
$w = w_0 \Big[ 1+ \sin \Big(\frac{\pi x}{2l_B} \Big) \Big]$
donde w₀ = 1 000 lbs/ft y T₀. = 0.588345x10⁶.
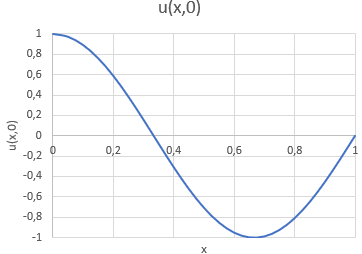
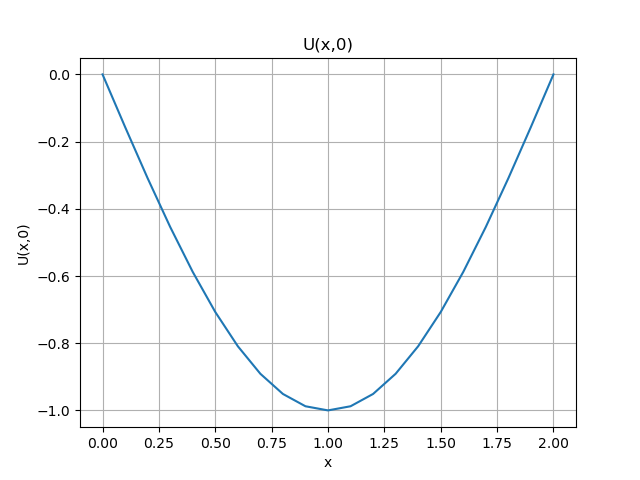
La pendiente del cable (dy/dx) = 0 en x = 0, que es el punto más bajo del cable.

También es el punto donde la tensión del cable alcanza un mínimo de T₀. La ecuación diferencial que gobierna el cable es
$\frac{d^2y}{dx^2} = \frac{w_0}{T_0} \Big[ 1+ \sin \Big(\frac{\pi x}{2l_B} \Big) \Big]$
a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para y(x) con tamaño de paso h=0.5

c. Usando el algoritmo, aproxime la solución para x en el intervalo entre [0,200], adjunte sus resultados.txt en la evaluación.

d. Realice sus observaciones sobre los resultados obtenidos sobre la altura y(200) alcanzada en el extremo derecho del cable y lo indicado en la gráfica del enunciado.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c resultados.txt (10 puntos), grafica.png (5 puntos), literal d (5 puntos),

Referencia: Cable entre dos apoyos con carga distribuida. Chapra & Canale. 5ta Ed. Ejercicio 28.21. P849

2024-01-31
2Eva_2023PAOII_T1 Volumen por solido de revolución

2da Evaluación 2023-2024 PAO II. 30/Enero/2024

Tema 1 (30 puntos) Los sólidos de revolución se generan al girar una región plana alrededor de un eje.
$V = \int_{a}^{b} \pi (f(x))^2 dx$
El volumen generado al girar la región de la función f(x) en el intervalo [a,b], se puede calcular como el volumen del disco de radio f(x) y anchura dx.
$f(x) = \sqrt{\sin (x/2)}$ $g(x) = e^{x/3} - 1$
Calcule el volumen de revolución generado por la región sombreada de la gráfica que ese encuentra entre: f(x) y g(x).
Las funciones se usan en el intervalo [0.1 , 1.8]:

Realice el planteamiento de las ecuaciones para el ejercicio, considerando que

a. Para el integral con f(x), use formulas de Simpson con al menos 3 tramos, mientras que

b. Para el integral con g(x) use Cuadratura de Gauss de dos puntos con al menos 2 tramos.

c. Desarrolle las expresiones completas del ejercicio para cada función.

d. Indique el resultado obtenido para el área requerida y la cota de error.

e. Determine el volumen de revolución generado por la región sombreada

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: [1] Volúmenes de sólidos de revolución. Moisés Villena Muñoz.Capítulo 4 p78. https://www.dspace.espol.edu.ec/bitstream/123456789/4800/4/7417.pdf
[2] 8.2.2 Gráficas en 3D en Python, sólidos de revolución. http://blog.espol.edu.ec/ccpg1001/graficas-en-3d-en-python-sistema-de-ecuaciones-y-planos/
[3] Volumes: Washer Method Animation 2. Stacey Roshan. 24 Abril 2016.

2024-01-31
2Eva_2023PAOI_T3 EDP elíptica, placa rectangular con frontera variable

2da Evaluación 2023-2024 PAO I. 29/Agosto/2023

Tema 3 (35 puntos) Aproxime la solución de la Ecuación Diferencial Parcial
$\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = \Big( x^2 + y^2 \Big) e^{xy}$ $0 \lt x \lt 1$ $0 \lt y \lt 0.5$
Con las condiciones de frontera:

u(0,y)=1, u(1,y)= y, 0≤y≤0.5
u(x,0)=1, u(x,0.5)=x/2, 0≤x≤1

Aproxime la solución con tamaños de paso Δx = 0.25, Δy = 0.25
Utilice diferencias finitas centradas para las variables independientes x,y

a. Plantee las ecuaciones para usar un método numérico en un nodo i,j

b. Realice la gráfica de malla,

c. desarrolle y obtenga el modelo discreto para u(x_i,t_j)

d. Realice al menos tres iteraciones en el eje tiempo.

e. Estime el error de u(x_i,t_j) y adjunte los archivos del algoritmo y resultados.

Rúbrica: Aproximación de las derivadas parciales (5 puntos), construcción de la malla (10), construcción del sistema lineal (15), resolución del sistema (5 puntos).

Referencia: 2Eva_IT2012_T3 EDP elíptica, placa rectangular

2023-08-31
2Eva_2023PAOI_T2 EDO Péndulo vertical amortiguado

2da Evaluación 2023-2024 PAO I. 29/Agosto/2023

Tema 2 (35 puntos) Una mejor aproximación a un péndulo oscilante con un ángulo θ más amplio y con un coeficiente de amortiguamiento μ se expresa con una ecuación diferencial ordinaria de segundo orden.

$\frac{d^2 \theta}{dt^2} = -\mu \frac{d\theta}{ dt}-\frac{g}{L}\sin (\theta)$

g = 9.81 m/s²
L = 2 m
θ(0) = π/4 rad
θ' (0) = 0 rad/s

El péndulo se suelta desde el reposo, desde un ángulo de π/4 respecto al eje vertical. El coeficiente de amortiguamiento μ=0.5 es proporcional a la velocidad angular.

a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para θ(t) con tamaño de paso h=0.2

c. Usando el algoritmo, aproxime la solución entre t=0 a t=10 s, adjunte sus resultados en la evaluación.

d. Realice una observación sobre el movimiento estimado del péndulo a lo largo del tiempo.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (10 puntos), literal d (5 puntos)

Referencia: 2Eva_IT2019_T2 Péndulo vertical

Vista general de ecuaciones diferenciales I Capítulo 1, 6min 54s. 3Blue1Brown 31-Marzo-2023.

2023-08-31
2Eva_2023PAOI_T1 Material para medalla de academia

2da Evaluación 2023-2024 PAO I. 29/Agosto/2023

Tema 1 (30 puntos)
Una academia encarga a un joyero un modelo de medalla cuyo costo unitario se determina por el área descrita entre las funciones f(x) y g(x) presentadas.

Se considera que el grosor de la medalla es único e independiente de la forma de la medalla.
$f(x) = 2-8\Big( \frac{1}{2} - x \Big)^2$ $0 \le x \lt 1$ $g(x) = -\Big( 1-x\Big)\ln \Big( 1- x \Big)$
Para el desarrollo numérico, use diferentes métodos de Simpson para cada función.

a. Realice el planteamiento de las ecuaciones para el ejercicio.

b. Describa el criterio usado para determinar el número de tramos usado en cada caso.

c. Desarrolle las expresiones completas del ejercicio para cada función.

d. Indique el resultado obtenido para el área requerida y la cota de error.

e. Encuentre el valor del tamaño de paso si se requiere una cota de error de 0.00032

Nota: en Python ln(x) se escribe np.log(x).

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: Star Trek https://intl.startrek.com/
¿A quien se le ocurrió crear la moneda? | Discovery en Español Youtube.com 8 nov 2016.

2023-08-31
2Eva_2022PAOII_T3 EDP Parabólica con coseno 3/4π

2da Evaluación 2022-2023 PAO II. 24/Enero/2023

Tema 3. (35 puntos) Aproxime la solución a la siguiente ecuación diferencial parcial parabólica
$\frac{\partial^2 u}{\partial x^2} = b \frac{\partial u}{\partial t}$
Con las siguientes condiciones de frontera:
u(0,t)=1
u(1,t)=0

Y las condiciones iniciales
$u(x,0) = \cos \Big( \frac{3π}{2}x\Big)$

Utilice diferencias finitas centradas para x, para t hacia adelante.

a. Plantee las ecuaciones para usar un método numérico en un nodo i,j
b. Realice la gráfica de malla,
c. desarrolle y obtenga el modelo discreto para u(xi,tj)

Suponga que b = 2, Aproxime la solución con Δx = 0.2, Δt = Δx/100.

d. Realice al menos tres iteraciones en el eje tiempo.
e. Estime el error de u(xi,tj), y presente observaciones sobre la convergencia del método.

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (15 puntos), literal e (5 puntos).

Referencia: Chapra & R. Canale (2010). Métodos Numéricos para Ingenieros. Ejercicio 30.15 p904,
Solving the heat equation | DE3. 3Blue1Brown 16 Junio 2019.

2023-01-24
2Eva_2022PAOII_T2 EDO - población de protestantes en una sociedad

2da Evaluación 2022-2023 PAO II. 24/Enero/2023

Tema 1. (35 puntos) En el libro titulado “Looking at History Through Mathematics”, Rashevsky propone un modelo que se puede relacionar con el “protestantismo” en el siglo XVI como una reacción y denuncia de abusos impuestos sobre la sociedad de la época.

En un modelo de Rashevsky modificado con la ecuación logística de Verhulst, la población x(t) de individuos en la sociedad para cada año t, con tasas de natalidad b=0.02 y mortalidad d=0.015, cambia según la ecuación:
$\frac{\delta}{\delta t}x(t) = b x(t) - d (x(t))^2$ $x(0)=1$
La cantidad de individuos “protestantes” y(t) en la población se incrementa según la ecuación diferencial compuesta de dos términos.
$\frac{\delta}{\delta t}y(t) = b y(t) - d (y(t))^2 +r b (x(t)-y(t))$ $y(0)=0.01$
El primer término supone que todas familias de padre y madre “protestantes” tienen hijos que también se identifican como tales.

El segundo término supone que una porción r = 0.1 de jóvenes descendientes de los “conformistas” al meditar sobre la situación actual, los hechos y los argumentos de protesta se convierten a “protestantes”.

a.       Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b.       Desarrolle tres iteraciones para x(t), y(t) con tamaño de paso h=0.5.

c.       Usando el algoritmo, aproxime la solución entre t=0 a t=200 años, adjunte sus resultados en la evaluación.

d.       Realice una observación sobre el crecimiento de población y(t) a lo largo del tiempo.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (10 puntos), literal d (5 puntos)

Referencia: Burden 5.2 Ejercicio 17 p276, Rashevsky, MIT 1968. pp102-110, Protestantismo https://es.wikipedia.org/wiki/Protestantismo. 3Eva_IIT2014_T2 Crecimiento demográfico. http://blog.espol.edu.ec/analisisnumerico/3eva_iit2014_t2-crecimiento-demografico/

La Reforma protestante y Lutero. Academia Play. 27 agosto 2019

2023-01-24
2Eva_2022PAOII_T1 Altura de cohete en 30 segundos

2da Evaluación 2022-2023 PAO II. 24/Enero/2023

Tema 1. (30 puntos) La velocidad hacia arriba de un cohete se calcula con la fórmula:
$v = u \ln\Big(\frac{m_0}{m_0-qt}\Big) - gt$
Donde:
v   = velocidad hacia arriba,
u   = 1800 m/s, velocidad a que se expele el combustible en relación con el cohete,
m₀ = 160 000 kg, masa inicial del cohete en el tiempo t = 0,
q    = 2 500 kg/s, tasa de consumo de combustible y
g    = 9.8 m/s2, aceleración de la gravedad

Para determinar la altura alcanzada por el cohete en un vuelo de 30 segundos desarrolle la parte analítica con los siguientes métodos y compare los resultados.

a. Utilice la regla de Simpson, en el planteamiento incluya la cantidad de tramos o segmentos a usar

b. Use el método de cuadratura de Gauss para la misma cantidad de segmentos que el literal anterior

c. Compare y comente los resultados, sobre los errores entre los métodos.

Rúbrica: Planteamiento de tramos (5 puntos), integral con Simpson (10 puntos), cuadratura de Gauss (10 puntos), literal c (5 puntos).

Referencia: Chapra ejercicio 24.46 p701. NASA y SpaceX realizan con éxito el despegue del primer vuelo de EE. UU. hacia la Estación Espacial Internacional en nueve años. EFE 30 mayo 2020 https://youtu.be/npcgpQUKAbg

2023-01-24
2Eva_2022PAOI_T3 EDP parabólica barra enfriada en centro

2da Evaluación 2022-2023 PAO I. 30/Agosto/2022

Tema 3. (40 puntos) Use el método de diferencias progresivas para aproximar la solución de la siguiente ecuación diferencial parcial parabólica:
$\frac{\partial U}{\partial t} - \frac{1}{9} \frac{\partial ^2 U}{\partial x^2} = 0$ $0 \leq x \leq 2, t>0$
Con las condiciones iniciales de borde e iniciales:
$U(0,t) = U(2,t) = 0, t>0$ $U(x,0) = \cos \Big( \frac{\pi}{2}(x-3)\Big) , 0 \leq x \leq 2$
Aplique un método numérico para encontrar los valores de U(x,t) usando Δx = 1/3, Δt = 0.02 y muestre:

a. La grafica de malla
b. Ecuaciones de diferencias divididas a usar
c. Encuentre las ecuaciones considerando las condiciones dadas en el problema.
d. Determine el valor de λ, agrupando las constantes durante el desarrollo, revise la convergencia del método.
e. Resuelva para tres pasos
f. Estime el error (solo plantear)
g. Usando el algoritmo, aproxime la solución para t=0.02 y t=0.1

Rúbrica: literal a (3 puntos), literal b (2 puntos), literal c (5 puntos), literal d (5 puntos), aplicación de condiciones iniciales (5 puntos), literal e (10 puntos), literal f (5 puntos). literal g, usando algoritmo (5 puntos)

Referencia: 2Eva_IT2017_T3 EDP parabólica http://blog.espol.edu.ec/analisisnumerico/2eva_it2017_t3-edp-parabolica/

2022-08-31
2Eva_2022PAOI_T2 EDO de circuito RLC con interruptor intermedio

2da Evaluación 2022-2023 PAO I. 30/Agosto/2022

Tema 2. (30 puntos) El circuito de la figura 2a tiene el interruptor en posición cerrada por largo tiempo antes de t=0, con lo que la corriente en el inductor será de 2 Amperios, y(0)=2. Para t<0, el inductor opera como un conductor sin caída de voltaje, el capacitor está cargado a 10V y solo pasaría corriente por la resistencia de 5 Ohm.

En el tiempo t=0, el interruptor se abre de forma instantánea y el circuito cambia al modelo de la figura 2b.

La corriente del inductor y(t) para t≥0 está dada por la ecuación:
$\frac{\delta}{\delta t}y(t) + 2 y(t) + 5 \int_{-\infty}^t y(\tau) \delta \tau = 10 \mu(t)$
En t=0, luego de abrir el interruptor, los voltajes de la fuente y el capacitor son iguales. La corriente inicial sobre el resistor de 2 A genera un voltaje que se compensa con el voltaje del inductor pero en signo opuesto. Lo que implica que y’(0) = -4
$V_{Inductor} = - V_{resistor}$ $y'(0) = -4$
Derive la expresión de corrientes y(t) para obtener una ecuación diferencial ordinaria.

a) Realice el planteamiento del problema usando el método de Runge-Kutta de 2do orden para 2da derivada

b) Desarrolle las expresiones para al menos tres iteraciones usando h=0.01

c) Estime el valor del error.

d) Muestre el resultado con el algoritmo para el intervalo t entre [0,5] segundos

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos)

Referencia: Lathi B.P. Green R. Linear Systems and Signals, 3rd Edition. ejemplo 4.13 p364

2022-08-31