Curso con Python – MATG1052-FCNM-ESPOL
Tema 2. (20 puntos) El meteorólogo Edward Lorenz propuso inicialmente el siguiente sistema para predecir el comportamiento del clima:
Para su estudio eligió los parámetros α = 10, β = 8/3 , ρ=28 con las condiciones iniciales x(0) = 10, y(0) = 7, z(0) = 7
Use el método de Runge-Kutta clásico de cuarto orden con h = 0.25 para calcular la solución cuando t=1
Referencia: Chapra 28.2 p833 pdf857
Tema 1. (20 puntos) 
La trayectoria de un teleférico está definida por una curva que tiene los puntos (x, f(x)) segun la tabla que se muestra a continuación:
x = [ 0.00, 0.25, 0.50, 0.75, 1.00] f(x) = [25.00, 22, 45, 62, 75 ]
Para calcular la longitud de dicha curva se debe usar la integral:
a. Aproxime el valor de f'(x) pra cada uno de los valores de x de la tabla
b. Aproxime el valor de la longitud del cable usando el método de Simpson
Tema 3. (40 puntos) Dados los puntos
(x,y): (2,3), (4,4), (5,6), (6,7), (8,5)
Use el trazador cúbico natural para determinar el valor de y cuando x=3.
Use el método iterativo de Gauss-Seidel para resolver el sistema de ecuaciones que se produce al aplicar la formulación del trazador cúbico.
Comience con un vector solución nulo e itere hasta obtener tres decimales exactos.
xi = [ 2, 4, 5, 6, 8] yi = [ 3, 4, 6, 7, 5]
Tema 2. (30 puntos) Utilizando los 9 datos de las cuadrículas centrales de la tabla anterior, calcule aproximadamente la profundidad del lago en el punto de coordenadas x = 250, y = 125
Utilice en ambas direcciones el polinomio de Lagrange o el polinomio de diferencias finitas y estime el error en la interpolación.
| y\x | 0 | 100 | 200 | 300 | 400 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 4 | 6 | 0 |
| 50 | 0 | 3 | 5 | 7 | 3 |
| 100 | 1 | 5 | 6 | 9 | 5 |
| 150 | 0 | 2 | 3 | 5 | 1 |
| 200 | 0 | 0 | 1 | 2 | 0 |
profundidad= [[ 0, 0, 4, 6, 0],
[ 0, 3, 5, 7, 3],
[ 1, 5, 6, 9, 5],
[ 0, 2, 3, 5, 1],
[ 0, 0, 1, 2, 0]]
x = [ 0, 100, 200, 300, 400]
y = [ 0, 50, 100, 150, 200]
Tema 1. (30 puntos) Un lago tiene la forma aproximadamente rectangular de 200 m x 400 m.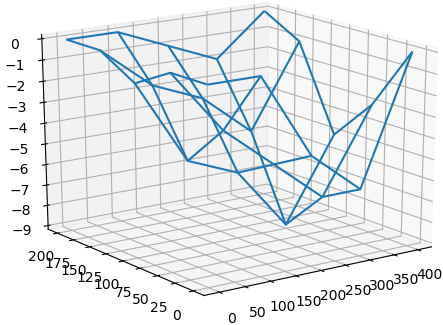
Se ha trazado un cuadriculado y se ha medido la profundidad en metros en cada cuadrícula de la malla como se
| y\x | 0 | 100 | 200 | 300 | 400 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 4 | 6 | 0 |
| 50 | 0 | 3 | 5 | 7 | 3 |
| 100 | 1 | 5 | 6 | 9 | 5 |
| 150 | 0 | 2 | 3 | 5 | 1 |
| 200 | 0 | 0 | 1 | 2 | 0 |
con todos los 25 datos de la tabla, estime el volumen aproximado de agua.
Utilice la fórmula de Simpson en ambas direcciones.
profundidad= [[ 0, 0, 4, 6, 0],
[ 0, 3, 5, 7, 3],
[ 1, 5, 6, 9, 5],
[ 0, 2, 3, 5, 1],
[ 0, 0, 1, 2, 0]]
x = [ 0, 100, 200, 300, 400]
y = [ 0, 50, 100, 150, 200]
Tema 3. Aproxime la solución de la ecuación diferencial parcial:
t> 0 , 0≤ x ≤ 1
Con h= 0.25 y k=0.04, realizar solo dos iteraciones en el tiempo (j=1,2) .
Indicación: Para establecer el algoritmo, utilice la fórmula progresiva para la primera derivada.
Tema 2. Resolver el problema de valor inicial:
a. Escribir el algoritmo de Runge-Kutta de cuarto orden para la función específica f(x,y).
b. Escribir una tabla de resultados, con h=0.2
Tema 1. Aproximar la siguiente integral:
Usar Simpson con n=6
Tema 3. Con respecto a los datos del Tema 2, aproxime la integral de g(x) con el método de la cuadratura de Gauss de dos términos usando n = 1, 2, 3 subintervalos.
Con éstos resultados estime la precisión de la respuesta del integral.
Previamente debe usar los datos para aproximar g(x) mediante un polinomio de interpolación.
Tema 2. Sea la función y = f(x), 0≤x≤2, con los nodos xi y los valores f( xi ), como se indica:
| x | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 |
| y=f(x) | 0.0 | 0.8 | 0.9 | 0.7 | 0.3 |
Se requiere evaluar la siguiente integral relacionada con los datos dados:
Aproxime la integral de g(x) con el método de Simpson 1/3, con n=4 subintervalos.
Previamente obtenga los puntos de g(x) aproximando el valor de la derivada y’ con una fórmula de orden 2.
Estime el error en la aproximación de la derivada.
xi = [ 0.0, 0.5, 1.0, 1.5, 2.0] yi = [ 0.0, 0.8, 0.9, 0.7, 0.3]