Algoritmos101

Cursos Python

Categoría: 3ra Evaluación

  • 3Eva_IT2018_T1 Intersección de dos círculos

    3ra Evaluación I Término 2018-2019. 11/Septiembre/2018. MATG1013

    Tema 1. (30 puntos) Encuentre las raíces de las ecuaciones simultaneas siguientes:

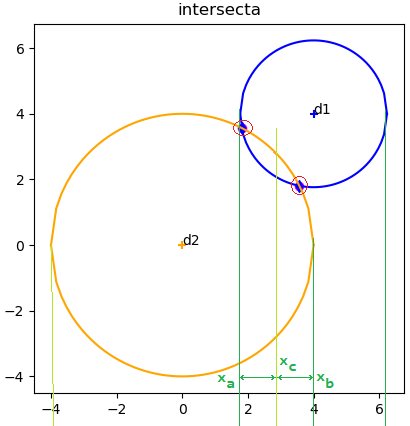
    (x-4)^2 + (y-4)^2 = 5 x^2 + y^2 = 16

    a) Use el enfoque gráfico para obtener los valores iniciales.

    b) Encuentre aproximaciones refinadas con el Método de Newton-Raphson

    Rúbrica: literal a (10 puntos), literal b  (20 puntos)

    intersecta Circulos 01

    Referencia: Un asteroide dos veces más grande que un avión Boeing 747 pasará muy cerca la Tierra. https://www.eluniverso.com/noticias/2018/08/28/nota/6927335/asteroide-dos-veces-mas-grande-que-avion-pasara-muy-cerca-tierra

    Intersecta Circulos 02
    Europa Press 28 de agosto, 2018 - 11h51

  • 3Eva_IIT2017_T4 EDO con valor inicial Taylor 2do Orden

    3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

    Tema 4. Use el método de Taylor de orden 2 para aproximar la solución de EDO con valor inicial

    y'= -ty + \frac{4t}{y} 0 \leq t \leq 1 y(0) = 1, h = 0.2

    a. Plantear el ejercicio

    b. Desarrolle 3 iteraciones o pasos,

    c. Estime el error para las iteraciones

  • 3Eva_IIT2017_T3 EDP Elíptica, placa rectangular

    3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

    Tema 3. Aproxime la solución de la siguiente EDP elíptica.

    \frac{\partial^2 u}{\partial x^2} + \frac{\partial ^2u}{\partial y^2} = (x^2 + y^2) e^{xy} 0 \lt x \lt 2, 0 \lt y \lt 1

    con condiciones de frontera

    u(0,y) = 1 , u(2,y) = e^{2y}, 0 \leq y \leq 1 u(x,0) = 1, u(x,1) = e^x , 0 \leq x \leq 2

    a) use tamaños de paso h = 2/3 y k = 1/3

    b) compare con la solución u(x,y) = exy en forma gráfica

  • 3Eva_IIT2017_T2 Carrera de caballos - interpolar

    3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

    Tema 2. El caballo llamado Thunder Gulch ganó el derby de Kentucky de 1995, con un tiempo de 2 min 1 \frac{1}{5} s en la carrera de 1 \frac{1}{4} millas. caballo carreras 01

    Los tiempos en los postes que marcan el cuarto de milla, la mitad de la milla y la milla fueron respectivamente 22 \frac{2}{5} s, 45 \frac{4}{5} s, 1 min con 1 \frac{1}{5} s.

    a) Use los valores anteriores junto con el tiempo de arranque y construya un trazador cúbico natural.

    b) Use el trazador para predecir el tiempo en el poste de tres cuartos de milla y compare el resultado con el tiempo real de 1 min con 10 \frac{1}{5} s.

    c) Usando el trazador y las fórmulas de diferencias finitas, aproxime la velocidad y la aceleración del caballo en todos los postes.

    Nota: Obseve que las medidas se encuentran en fracciones de unidad.

  • 3Eva_IIT2017_T1 Punto fijo

    3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

    Tema 1. Sea g: [a,b] →ℜe (reales) una función diferenciable tal que g(x) ∈ [a,b], para toda x ∈ [a,b]. Demuestre o refute las siguientes afirmaciones.

    a) g tiene al menos un punto fijo en [a,b]

    b) g tiene un punto fijo único en [a,b]

  • 3Eva_IT2017_T4 EDP elíptica, placa desplazada

    3ra Evaluación I Término 2017-2018. 11/Septiembre/2017. MATG1013

    Tema 4.  Aproxime la solución de la EDP elíptica:

    \frac{\partial ^2 U}{\partial x^2} + \frac{\partial ^2 U}{\partial y^2} = \frac{x}{y} + \frac{y}{x}

    1 <  x < 2
    1 <  y < 2

    U(x,1)= x \ln (x), U(x,2) = x \ln (4x^{2}),1 \lt x \lt 2 U(1,y)= y \ln(y), U(2,y) = 2y \ln (2y), 1 \lt x \lt 2

    use h = k = 0.5

  • 3Eva_IT2017_T3 Sustancia en lago

    3ra Evaluación I Término 2017-2018. 11/Septiembre/2017. MATG1013

    Tema 3. El área de la sección transversal As (m2) de un lago, a cierta profundidad, se calcula a partir del volumen utilizando la diferenciación:

    A_s(Z) = -\frac{\delta V}{\delta z} (Z)

    Donde V = volumen (m3) y z = profundidad (m), se mide a partir de la superficie en dirección del fondo.

    La concentración promedio de una sustancia que varía con la profundidad \overline{c} (g/m3) se obtiene por integración:

    \overline{c} = \frac{\int_0^{Z_t} c(Z) A_s(Z) \delta Z}{\int_0^{Z_t}A_s(z) \delta Z}

    Donde Zt es la profundidad total (m).
    Determine la concentración promedio con base en los siguientes datos:

    z (m)  0  4 8 12 16
    V (106 m3)  9.82 5.11 1.96 0.393 0.000
    c (g/m3)  10.2  8.5  7.4 5.2 4.1

    Sustancia Lago 01

    zi = [0.  , 4   , 8   , 12    , 16]
vi = [9.82, 5.11, 1.96,  0.393,  0.]
ci = [10.2, 8.5 , 7.4 ,  5.2  ,  4.1]

  • 3Eva_IT2017_T2 EDO Runge-Kutta d3y/dx3

    3ra Evaluación I Término 2017-2018. 11/Septiembre/2017. MATG1013

    Tema 2. Use un método de Runge Kutta para sistemas y aproxime la solución de la siguiente EDO de orden superior

    y'''+ 2y'' - y'- 2y = e^t

    0 ≤ t ≤ 1

    y(0) = 1
    y'(0) = 0
    y''(0) = 0

    con h = 0.25

  • 3Eva_IT2017_T1 Crecimiento de levadura

    3ra Evaluación I Término 2017-2018. 11/Septiembre/2017. MATG1013

    Tema 1. La razón de crecimiento específico g de una levadura que produce un antibiótico es una función de la concentración del alimento c,

    g = \frac{2c}{4+0.8c + c^2 +0.2 c^3}

    Como se ilustra en la figura, el crecimiento parte de cero a muy bajas concentraciones debido a la limitación de alimento.

    También parte de cero en altas concentraciones debido a los efectos de toxicidad.

    a) Encuentre el valor de c para el cual el crecimiento es un máximo.

    b) Evalúe la función g del problema 1 para c=0,1,2,3, y encuentre el trazador cúbico natural para aproximar el máximo de g, encuentre el error.

  • 3Eva_IT2015_T4 Fórmula central de orden 2

    3ra Evaluación I Término 2015-2016. 22/Septiembre/2015. ICM00158

    Tema 4. Dados los puntos x0, x1 y x2, con h constante y sus respectivas imágenes.

    Deduzca la fórmula central de orden 2 para aproximar la segunda derivada en el punto x1 y estime el error.