Algoritmos101

Cursos Python

Categoría: Evaluaciones

Ejercicios de examen

  • 2Eva_IIT2019_T1 Canteras y urbanizaciones

    2da Evaluación II Término 2019-2020. 28/Enero/2020. MATG1013

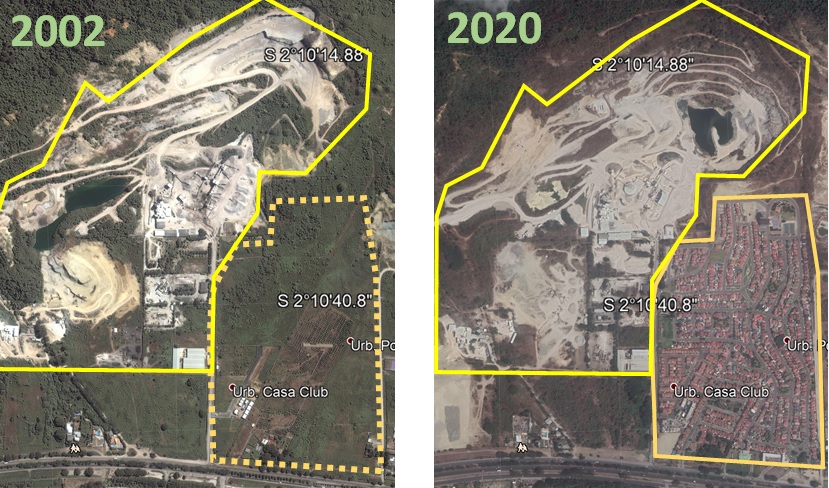
    Tema 1. (20 Puntos) En el conflicto presentado entre las urbanizaciones y canteras en vía a la costa, se menciona que se ha afectado al ecosistema al disminuir la vegetación en la zona.

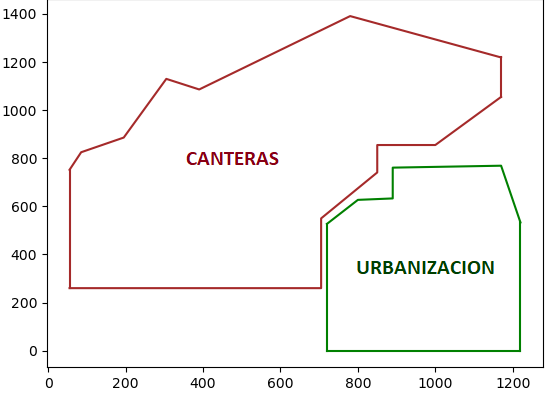
    Una forma de observar el cambio en la zona es medir el área ocupada por cada actor.

    Cantera Urbaniza 01

    Para la observación considere que la superficie ocupada por las urbanizaciones y canteras se describe con los siguientes datos de frontera:

    Cantera Urbaniza 02

    Canteras- frontera superior
    xi 55 85 195 305 390 780 1170
    f(xi) 752 825 886 1130 1086 1391 1219
    Canteras- frontera inferior
    xi 55 ... 705 705 850 850 1010 1170
    f(xi) 260 ... 260 550 741 855 855 1055
    Urbanización - frontera superior
    xi 720 800 890 890 1170 1220
    g(xi) 527 630 630 760 760 533
    Urbanización - frontera inferior
    xi 720 ... 1220
    g(xi) 0 ... 0

    Nota: Observe que los tamaños de paso no son todos regulares

    Usando el método del trapecio, determine:

    a) El área de operación de la cantera

    b) El área ocupada por la urbanización

    c) ¿Se puede mejorar la precisión del cálculo de las áreas, sin quitar o aumentar datos? Justifique su respuesta e indique cómo y dónde.

    Rúbrica: literal a (5 puntos), literal b(5 puntos), literal c: cómo (5 puntos), dónde(5 puntos)

    Referencia: Google Maps Enero 2019.
    Dos bosques cercados por el crecimiento de Guayaquil. 27- Julio-2014.
    https://www.eluniverso.com/noticias/2014/07/27/nota/3282036/dos-bosques-cercados-urbe-que-crece
    La remediación ambiental en vía a la costa tomará giro legal. 02-Enero-2020.
    https://www.expreso.ec/guayaquil/remediacion-ambiental-via-costa-tomara-giro-legal-2518.html

  • 1Eva_IIT2019_T1 Ecuación Recursiva

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 1. (30 puntos). Considere la sucesión

    \Big( x_n \Big)_{n=0}^{+ \infty}

    cuya ecuación recursiva es:

    x_n = g(x) = \sqrt{3 + x_{n-1}}

    para n  ∈ Ν

    a) ¿Se puede afirmar que ∀x ∈ [1,3], g(x) ∈ [1,3]?

    b) Pruebe que g es una función contractiva en el intervalo [1,3] y estime el valor de la constante de Lipschitz (cota de la derivada de g)

    c) Realice 5 iteraciones partiendo del dato inicial x0 =2, y determine el orden de convergencia.

    d) Encuentre el valor teórico de x* al cual converge la sucesión y estime el error absolito en la iteración 5.

    e) Realice 5 iteraciones con el método de bisección en el intervalo [1,3] para aproximar el punto fijo de la función g(x).

    Rúbrica: literal a (3 puntos), literal b (3 puntos), literal c (10 puntos), literal d (4 puntos), literal e (10 puntos)

    Referencia: Burden 9Ed. Definición 10.5 p633, Theorem 2.4 P62;
    Contracción https://es.wikipedia.org/wiki/Contracci%C3%B3n_(espacio_m%C3%A9trico).
    Función lipschitziana https://es.wikipedia.org/wiki/Funci%C3%B3n_lipschitziana

     

  • 1Eva_IIT2019_T2 Proceso Termodinámico

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 2. (20 puntos).  Para simular la disminución de la temperatura en un proceso termodinámico, mechero calienta una barra
    un algoritmo evolutivo necesita usar un polinomio para aproximar en el intervalo [0,4] la función f con regla de correspondencia

    f(x)=e^{-0.5x}

    con constante k = 0.5

    Para construir el mencionado polinomio, considere la tabla:

    x 0 1 2 3 4
    f(x) f(0) f(1) f(2) f(3) f(4)

    a. Aplique interpolación polinomial y aproxime el valor de f(2.4) usando un polinomio de grado 2.

    b. Encuentre una cota superior para el error de interpolación en la aproximación de f(1.7)}

    Rúbrica: literal a (15 puntos), literal b (5 puntos)

  • 1Eva_IIT2019_T3 Circuito eléctrico

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 3. (30 puntos) El sistema de ecuaciones que sigue se generó por medio de aplicar la ley de malla de corriente al circuito de la figura. circuito eléctrico con resistencias y fuentes

    \begin{cases} 55 I_1 - 25 I_4 = -200 \\ -37 I_3 - 4 I_4 = -250 \\ -25 I_1 - 4 I_3 + 29 I_4 = 100 \end{cases}

    a) Use el método de eliminación de Gauss para calcular I1, I3, I4, I1 observando que
    I2 = -10

    b) Encuentre la norma infinita de la matriz de transición T en el método de Jacobi y comente.

    c) Con el método de Gauss-Seidel realice tres iteraciones comenzando con el vector cero. Además en la tercera iteración, encuentre una cota para el error relativo.

    Rúbrica: literal a (12 puntos), literal b (6 puntos), literal c (12 puntos)

    A = [[ 55.0, 0,  0, -25],
     [  0  , 0,-37,  -4],
     [-25  , 0, -4,  29],
     [  0  ,  1, 0,   0]]

B = [-200,-250,100,-10]

  • 1Eva_IIT2019_T4 Concentración de químico

    1ra Evaluación II Término 2019-2020. 26/Noviembre/2019. MATG1013

    Tema 4. (20 puntos) La siguiente ecuación permite calcular la concentración de un químico en un reactor, donde se tiene una mezcla completa.

    C = C_{ent} ( 1 - e^{-0.04t})+C_{0} e^{-0.03t}
    https://es.wikipedia.org/wiki/Reactor_qu%C3%ADmico

    Si la concentración inicial es C0 = 4 y la concentración de entrada es Cent = 10, use el método de Newton-Raphson con t0 = 0, para aproximar el tiempo requerido para que el valor de C sea 93% de Cent.

    Encuentre un intervalo en donde la convergencia está garantizada.

    Rúbrica: intervalo (5 puntos), iteraciones (10 puntos), convergencia (5 puntos)

  • 3Eva_IT2019_T3 EDP Difusión en sólidos

    3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

    Tema 3. (30 Puntos).  En el año 1855, los experimentos de Adolf Fick tratan sobre la medición de concentraciones y sus flujos, también ahora aplicados a la difusión en sólidos que en ese tiempo no se consideraba posible.

    Difusion En Solidos 01

    La gráfica muestra los cambios en el tiempo de concentración Φ de un gas en un sólido (estado no-estacionario) para un sólido semi infinito (eje y).

    La segunda ley de Fick predice la forma en que la difusión causa que la concentración cambie con el tiempo. Se trata de una ecuación diferencial parcial que en una dimensión se escribe:

    \frac{\partial \phi}{\partial t} = D\frac{\partial ^2 \phi}{\partial x^2}
    Φ(0, t) = 5
    Φ(L, t) = 0
    Φ(x,0) = 0    		 D = 0.16
    L =0.1

    a. Plantee las ecuaciones, la malla, desarrolle y obtenga el modelo Φ(xi,tj)

    b. Aproxime la solución con Δx = 0.02, Δt = Δx/100. Realice al menos tres iteraciones en el eje tiempo.

    c. Estime el error de Φ(xi,tj)

    Rúbrica: Construir la malla (5 puntos), plantear la ecuación en el nodo i,j (5 puntos), modelo de ecuación (5 puntos), literal b (10 puntos), literal c (5 puntos).

    Referencia: https://es.wikipedia.org/wiki/Leyes_de_Fick;
    Difusión 2ª Ley de Fick|7/22|UPV (2011) https://www.youtube.com/watch?v=HHBvZDNvTic

  • 3Eva_IT2019_T2 Integral con interpolación

    3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

    Tema 2. (40 Puntos) Construya un polinomio que aproxime a

    f(x) = sin(\pi x)

    usando los puntos x=0, π/4, π/2 y aproxime la integral de 0 a π/2.

    a. Realice la interpolación mediante el método de trazador cúbico fijo

    b. Integre usando el método de cuadratura de Gauss

    c. Estime el error para el ejercicio.

    Rúbrica: Bosquejo de gráficas (5 puntos), literal a, planteo de fórmulas (5 puntos), calcula los parámetros (10 puntos), literal b (15 puntos), literal c (5 puntos).

  • 3Eva_IT2019_T1 Ecuaciones simultáneas

    3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

    Tema 1. (30 Puntos).  Determine las raíces de las ecuaciones simultáneas siguientes:

    y = -x^2 +x + 0.75 y+5xy=x^3

    a. Realice un bosquejo para cada ecuación
    b. Use el método de Newton-Raphson con x0=1 , y0=0.75, realice 3 iteraciones
    c. Estime el orden del error

    Rúbrica: literal a (5 puntos), literal b planteo (5 puntos), iteraciones (15 puntos), literal c (5 puntos)

  • 2Eva_IT2019_T3 EDP Elíptica Placa 6x5

    2da Evaluación I Término 2019-2020. 27/Agosto/2019. MATG1013

    Tema 3. (30 Puntos) Una placa rectangular de plata de 6x5 cm tiene calor que se genera uniformemente en todos los puntos, con una rapidez q = 1.5 cal/cm3 s.

    Al representar con x la distancia a lo largo del borde de longitud 6 cm y con y la de 5 cm.

    Suponga que la temperatura en los bordes se mantiene como se indica:

    u(x,0) = x(6-x) u(x,5)=0 0≤x≤6
    u(0,y) = y(5-y) u(6,y)=0 0≤y≤5

    Donde el origen se encuentra en una esquina de la placa y los bordes se hayan a lo largo de los ejes positivos x, y.

    La temperatura de estado estable u(x,y) satisface la ecuación de Poisson:

    \frac{\partial^2 u}{\partial x^2} (x,y)+\frac{\partial ^2 u}{\partial y^2 } (x,y) = -\frac{q}{K}

    0≤x≤6
    0≤y≤5

    Donde K, la conductividad térmica es 1.04 cal/cm deg s.

    a. Aproxime la temperatura u(x,y) en los nodos de la malla con hx =2, hy= 2.5

    b. Exprese el término del error

    Rúbrica: literal a expresiones (10 puntos), valor (10 puntos), literal b (5 puntos)

    Referencia: Ejercicio 12.1.8, Burden 9Ed, p724.

  • 2Eva_IT2019_T2 EDO Péndulo vertical

    2da Evaluación I Término 2019-2020. 27/Agosto/2019. MATG1013

    Tema 2. (40 Puntos) Suponga que un péndulo tiene 0.6 m de Longitud, se desplaza θ desde la posición vertical de equilibrio.pendulo Vertical 01

    \frac{d^2\theta }{dt^2}+\frac{g}{L}\sin (\theta)=0 0\lt t \lt 1 g = 9.81 \frac{m}{s^2} \theta(0) = \frac{\pi}{6} \theta '(0) = 0

    a. Aproxime la solución de la ecuación para t = [0,1] con pasos de h=0.2
    b. Aproxime el valor del error

    Rúbrica: literal a, expresiones (20 puntos), valor (10 puntos), literal b (10 puntos)

    Referencia: Ejercicio 5.9.8, Burden 9Ed, p338.
    2Eva_IT2010_T2 Movimiento angular

    Professor of Physics Emeritus Walter Lewin.  Lec 11 | 8.01 Physics I: Classical Mechanics, Fall 1999.

    El PÉNDULO SIMPLE NO es como te explicaron | Física y Matemáticas. Mates Mike