2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numérico
Tema 4. Bono: Deduzca la fórmula de la derivada de y(x1) en función de y(x0), y(x1) y y(x2) considerando h constante.
Categoría: Evaluaciones
Ejercicios de examen
-
2Eva_IIT2016_T3_MN EDO Taylor 2, Tanque de agua
2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numérico
Tema 3. Si se drena agua desde un tanque cilíndrico vertical por medio de abrir una válvula en la base, el líquido fluirá rápido cuando el tanque está lleno y disminuye el flujo a medida que se drene.
Como se ve, la tasa a la que el nivel del agua disminuye es:
\frac{dy}{dt} = -k \sqrt{y}Donde k es una constante que depende de la forma del agujero y del área de la sección transversal del tanque y agujero del drenaje. La profundidad del agua del agua se mide en metros y el tiempo t en minutos.
Si k=0.06,
a) Determine en que tiempo la altura del nivel del agua llega a la mitad del nivel inicial que es 3 m. (Solo formule el método de Taylor de orden 2)
b) Realice 3 pasos con h=0.5 min
-
2Eva_IIT2016_T2_MN Volumen cacao seco
2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numérico
Tema 2. En una bodega de 4 m x 6m, hay una montaña de cacao seco listo para empaque.
La tabla indica la altura en metros de la montaña sobre el nodo en el plano medido al centímetro más cercano.
f(x,y) x=0 x=1 x=2 x=3 x=4 y=0 0.38 0.62 0.38 0.08 0.01 y=1.5 1.31 2.16 1.31 0.29 0.02 y=3 1.02 1.68 1.02 0.23 0.02 y=4.5 0.18 0.29 0.18 0.04 0.00 y=6 0.01 0.01 0.01 0.00 0.00 Use el método de Simpson 1/3 en ambas direcciones para aproximar el volumen V:
V = \int_0^4 \int_0^6 f(x,y)dydx
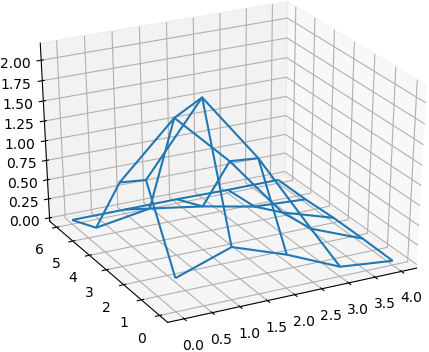
a) Realice la formulación del método indicando los puntos de la cuadrícula.
b) Estime la cota del error propagado y error total
Rúbrica: Planteamiento del problema (5 puntos), selección de método minimizando cotas de error (5 puntos), integración en un eje (5 puntos), integración en el otro eje (5 puntos), Estimación de errores (5 puntos)
x = [ 0.0, 1.0, 2.0, 3.0, 4.0] y = [ 0.0, 1.5, 3.0, 4.5, 6.0] fxy = [[0.38, 0.62, 0.38, 0.08, 0.01], [1.31, 2.16, 1.31, 0.29, 0.02], [1.02, 1.68, 1.02, 0.23, 0.02], [0.18, 0.29, 0.18, 0.04, 0.00], [0.01, 0.01, 0.01, 0.00, 0.00]] -
2Eva_IIT2016_T1_MN Coeficiente Gini
2da Evaluación II Término 2016-2017. 14/Febrero/2017. ICM02188 Métodos Numéricos
Tema 1. El coeficiente de Gini es una medida para medir la desigualdad.
G=\frac{a}{a+b}
Donde b es el área bajo la curva de Lorentz (Porcentaje de ingresos de las personas que menos ganan f(x) versus porcentaje de la población x, a + b = 0.5
Suponga que una población tiene los siguientes ingresos:
Datos de Población segmento (%) 20 20 20 20 20 Ingresos ($) 10000 20000 25000 30000 85000 a) Calcule los porcentajes acumulados y construya la función f(x) en función de x
(Curva de Lorentz)b) Aproxime b = \int_0^1 f(x) dx mediante el método del trapecio,
c) Estime el error
segmento = [ 20, 20, 20, 20, 20] ingresos = [ 10000, 20000, 25000, 30000, 85000]
Referencia: El coeficiente Gini, a partir del minuto 5:00, durante al menos 9:00
https://youtu.be/8sA7bRywTew?t=303
País de desigualdad (1/3) | DW Documental
-
1Eva_IT2016_T4_MN Conceptos
1ra Evaluación I Término 2016-2017. 28/junio/2016. ICM02188 Métodos Numéricos
Tema 4. (25 puntos) Responda las siguientes preguntas y justifique la respuesta
a) Si la ‖Tj‖∞ > 1 , entonces el método de Jacobi no converge
b) Si f ∈ C2[a,b] y p ∈ [a,b], tal que f(p)=0 y f '(p)≠0,
entonces existe δ > 0 tal que el método de Newton converge para cualquier
p0 ∈ [p - δ, p + δ]Rúbrica: literal a) falso (6 puntos), Justificación (6 puntos), literal b) verdadero (6 puntos), demostración (7 puntos)
-
2Eva_IT2015_T4 Deducir Simpson 1/3
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 4. (20 puntos) Utilizando el polinomio de grado 2, deduzca el método de Simpson 1/3.
-
2Eva_IT2015_T3 EDP parabólica
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 3. (30 puntos) Use el método de diferencias progresivas para aproximar la solución de la ecuación diferencial parcial parabólica
\frac{\partial u}{\partial t} - \frac{4}{\pi ^2}\frac{\partial ^2 u}{\partial x^2} = 0 0 \lt\ x \lt 4, 0\lt t u(0,t) = u(4,t) = 0, 0\lt t u(x,0) = \sin \Big( \frac{\pi}{4}x \Big) \Big( 1 + 2 \cos \Big( \frac{\pi}{4}x\Big)\Big) 0 \leq x \leq 4a) Use n=20 en el sentido de x; y m=10, obtenga el modelo (solo planteado).
b) Aproxime la solución con n=4, hasta 2Δt, y
c) estime el error en el punto P(x1, t1)
-
2Eva_IT2015_T1 Fibra óptica entre montañas
2da Evaluación I Término 2015-2016. 8/Septiembre/2015. ICM00158
Tema 1. (20 puntos) Para una fibra óptica que para por montañas se tienen las medidas de distancia vertical en función de la distancia horizontal y se muestra en la figura y la tabla.
distancias en metros horizontal x vertical y 0 0 100 25 200 38 300 45 400 20 a. Encuentre y' en los puntos de la tabla usando una aproximación de O(h2)
b. Usando La regla de Simpson 1/3 aproxime la longitud del cable y estime el error.
x = [ 0, 100, 200, 300, 400] y = [ 0, 25, 38, 45, 20]
-
3Eva_IT2015_T4 Fórmula central de orden 2
3ra Evaluación I Término 2015-2016. 22/Septiembre/2015. ICM00158
Tema 4. Dados los puntos x0, x1 y x2, con h constante y sus respectivas imágenes.
Deduzca la fórmula central de orden 2 para aproximar la segunda derivada en el punto x1 y estime el error.
-
3Eva_IT2015_T3 Poisson 3D
3ra Evaluación I Término 2015-2016. 22/Septiembre/2015. ICM00158
Tema 3. La ecuación de Poisson se puede escribir en tres dimensiones como
\frac{\partial ^2 T}{\partial x^2} + \frac{\partial ^2 T}{\partial y^2} + \frac{\partial ^2 T}{\partial z^2} = f(x, y ,z)a. Plantee las Temperaturas dentro de un cubo unitario con condiciones de frontera cero y f = -10. Utilice Δx = Δy = Δz = 1/3
b. Utilice el método de Gauss-Seidel para resolver el sistema en el literal a, (realice tres iteraciones y estime el error)
