Ejercicio: 2Eva_2025PAOI_T2 EDO Modelo económico de Solow-Swan
El modelo de crecimiento económico de Solow-Swan describe cómo el capital por trabajador k cambia con el tiempo dk/dt .
\frac{\delta k}{\delta t} = s f(k) -(d+n)k f(k) = k^{\alpha}literal a
La EDO es de primera derivada o primer orden, en la que se sustituyen los valore de las constantes y f(k)
f(t,k) = \frac{\delta k}{\delta t} = 0.15 k ^{0.3}-(0.05+0.015)kTiene como variable independiente el tiempo t, y como variable dependiente k.
Para evitar repetir la variable k en el algoritmo junto a Runge-Kutta, se cambia la variable por x:
f(t,y) = 0.15 y ^{0.3}-(0.05+0.015)yliteral b
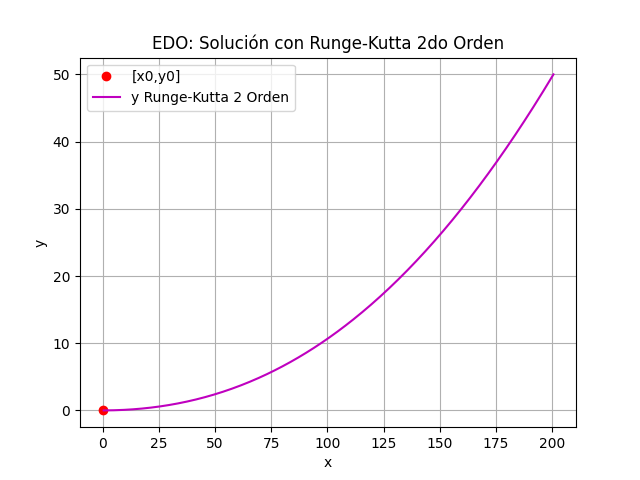
Desarrolle tres iteraciones con expresiones completas para k(t) con tamaño de paso h=0.2 meses, que se aplica al algoritmo EDO dy/dx con Runge-Kutta de 2do Orden
K_1 = h f(t_i,y_i) K_2 = h f(t_i+h, y_i + K_1) y_{i+1} = y_i + \frac{K_1+K_2}{2} t_{i+1} = t_i + hitera=0, ti= 0, yi=k(0)=1
K_1 = 0.2 \left( 0.15 (1) ^{0.3}-(0.05+0.015)(1) \right) =0.017 K_2 = 0.2 \left( 0.15 (1+0.017) ^{0.3}-(0.05+0.015)(1+0.017) \right) =0.016931 y_{1} = 1+ \frac{0.017+0.016931}{2} = 1.016966 t_{1} = 0 + 0.2 = 0.2itera = 1
K_1 = 0.2 \Big( 0.15 (1.016966) ^{0.3} -(0.05+0.015)(1.016966) \Big) =0.016931 K_2 = 0.2 \Big( 0.15 (1.016966+0.016931) ^{0.3} -(0.05+0.015)(1.016966+0.016931) \Big)=0.016861 y_{2} = 1.016966 + \frac{0.016931+0.016861}{2} =1.033862 t_{2} = 0.2 + 0.2 = 0.4itera = 2
K_1 = 0.2 \left( 0.15 (1.033862) ^{0.3}-(0.05+0.015)(1.033862) \right) =0.016861 K_2 = 0.2 \Big( 0.15 (1.033862+0.016861) ^{0.3} -(0.05+0.015)(1.033862+0.016861) \Big)=0.016789 y_{3} = 033862 + \frac{0.016861+0.016789}{2} t_{3} = 0.4 + 0.2 = 0.6Resultados con el algoritmo:
EDO dy/dx con Runge-Kutta 2 Orden i, [xi, yi, K1, K2] 0 [0. 1. 0. 0.] 1 [0.2 1.016966 0.017 0.016931] 2 [0.4 1.033862 0.016931 0.016861] 3 [0.6 1.050687 0.016861 0.016789] 4 [0.8 1.06744 0.016789 0.016716] 5 [1. 1.084119 0.016716 0.016642] 6 [1.2 1.100723 0.016642 0.016567] 7 [1.4 1.117252 0.016567 0.01649 ] 8 [1.6 1.133703 0.01649 0.016413] 9 [1.8 1.150077 0.016413 0.016334] 10 [2. 1.166371 0.016334 0.016255] ... 295 [5.900000e+01 3.121417e+00 1.647361e-03 1.632629e-03] 296 [5.920000e+01 3.123042e+00 1.632695e-03 1.618093e-03] 297 [5.940000e+01 3.124653e+00 1.618158e-03 1.603683e-03] 298 [5.960000e+01 3.126249e+00 1.603748e-03 1.589400e-03] 299 [5.980000e+01 3.127832e+00 1.589464e-03 1.575241e-03] 300 [6.000000e+01 3.129400e+00 1.575305e-03 1.561206e-03]
gráfica para 60 periodos completos con h=0.2
# EDO dy/dx. M todo de RungeKutta 2do Orden # estima la solucion para muestras espaciadas h en eje x # valores iniciales x0,y0, entrega tabla[xi,yi,K1,K2] import numpy as np def rungekutta2(d1y,x0,y0,h,muestras, vertabla=False,precision=6): '''solucion a EDO dy/dx, con Runge Kutta de 2do orden d1y es la expresi n dy/dx, tambien planteada como f(x,y), valores iniciales: x0,y0, tama o de paso h. muestras es la cantidad de puntos a calcular. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,2+2),dtype=float) tabla[0] = [x0,y0,0,0] # incluye el punto [x0,y0] xi = x0 # valores iniciales yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h tabla[i] = [xi,yi,K1,K2] if vertabla==True: np.set_printoptions(precision) print( 'EDO dy/dx con Runge-Kutta 2 Orden') print('i, [xi, yi, K1, K2]') for i in range(0,tamano,1): print(i,tabla[i]) return(tabla) # PROGRAMA PRUEBA ------------------- # INGRESO # d1y = y' = f, d2y = y'' = f' d1y = lambda t,k: 0.15*k**(0.3)-(0.05+0.015)*k x0 = 0 y0 = 1 h = 0.2 muestras = int(60/h) # PROCEDIMIENTO tabla = rungekutta2(d1y,x0,y0,h,muestras, vertabla=True) xi = tabla[:,0] yiRK2 = tabla[:,1] # SALIDA #print(' [xi, yi, K1, K2]') #print(tabla) # GRAFICA import matplotlib.pyplot as plt plt.plot(xi,yiRK2) plt.plot(xi[0],yiRK2[0], 'o',color='r', label ='[t0,k0]') ##plt.plot(xi[1:],yiRK2[1:], ## 'o',color='m', ## label ='[xi,yi] Runge-Kutta') plt.title('EDO dk/dt: Solow-Swan') plt.xlabel('t') plt.ylabel('k') plt.legend() plt.grid() plt.show()
.