Unidades - Página 3 - Métodos numéricos

2017-10-042025-09-07

7.1.2 EDP Parabólicas método implícito con Python

EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]

1. Ejercicio

Referencia: Chapra 30.3 p893 pdf917, Burden 9Ed 12.2 p729, Rodríguez 10.2.4 p415

Siguiendo el tema anterior en EDP Parabólicas, se tiene que:

\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}

EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]

2. Desarrollo Analítico

En éste caso se usan diferencias finitas centradas y hacia atrás; la línea de referencia es t₁:

\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2}

\frac{\partial u}{\partial t} = \frac{u_{i,j} - u_{i,j-1} }{\Delta t}

La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla.

Luego se sustituyen en la ecuación del problema, obteniendo:

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j}-u_{i,j-1}}{\Delta t}

De la gráfica se destaca que en la fórmula, dentro del triángulo solo hay DOS valores desconocidos, destacados por los punto en amarillo.
En la ecuación se representa por U[i,j] y U[i+1,j]. Por lo que será necesario crear un sistema de ecuaciones sobre toda la línea de tiempo t₁ para resolver el problema.

Despejando la ecuación, se agrupan términos constantes: $λ = \frac{\Delta t}{K (\Delta x)^2}$ .

\lambda u_{i-1,j} + (-1-2\lambda) u_{i,j} + \lambda u_{i+1,j} = -u_{i,j-1}

Los parámetro P, Q y R se determinan de forma semejante al método explícito:

P = \lambda

Q = -1-2\lambda

R = \lambda

Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j} = -u_{i,j-1}

Los valores en los extremos son conocidos, para los puntos intermedios se crea un sistema de ecuaciones para luego usar la forma Ax=B y resolver los valores para cada u(x_i,t_j).

Por ejemplo con cuatro tramos entre extremos se tiene que:
indice de tiempo es 1 e índice de x es 1.

i=1,j=1

Pu_{0,1} + Qu_{1,1} + Ru_{2,1} = -u_{1,0}

i=2,j=1

Pu_{1,1} + Qu_{2,1} + Ru_{3,1} = -u_{2,0}

i=3,j=1

Pu_{2,1} + Qu_{3,1} + Ru_{4,1} = -u_{3,0}

agrupando ecuaciones y sustituyendo valores conocidos:
$\begin{cases} Qu_{1,1} + Ru_{2,1} + 0 &= -T_{0}-PT_{A}\\Pu_{1,1} + Qu_{2,1} + Ru_{3,1} &= -T_{0}\\0+Pu_{2,1}+Qu_{3,1}&=-T_{0}-RT_{B}\end{cases}$

que genera la matriz a resolver:

\begin{bmatrix} Q && R && 0 && -T_{0}-PT_{A}\\P && Q && R && -T_{0}\\0 && P && Q && -T_{0}-RT_{B}\end{bmatrix}

Use alguno de los métodos de la unidad 3 para resolver el sistema y obtener los valores correspondientes.

Por la extensión de la solución es conveniente usar un algoritmo y convertir los pasos o partes pertinentes a funciones.

Tarea: Revisar y comparar con el método explícito.

EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]

Algoritmos en Python

Para la solución con el método implícito, se obtiene el mismo resultado en la gráfica y tabla. Aunque el algoritmo es diferente.

algunos valores:

iteración j: 1
A:
 [[-1.5   0.25  0.    0.    0.    0.    0.    0.    0.  ]
 [ 0.25 -1.5   0.25  0.    0.    0.    0.    0.    0.  ]
 [ 0.    0.25 -1.5   0.25  0.    0.    0.    0.    0.  ]
 [ 0.    0.    0.25 -1.5   0.25  0.    0.    0.    0.  ]
 [ 0.    0.    0.    0.25 -1.5   0.25  0.    0.    0.  ]
 [ 0.    0.    0.    0.    0.25 -1.5   0.25  0.    0.  ]
 [ 0.    0.    0.    0.    0.    0.25 -1.5   0.25  0.  ]
 [ 0.    0.    0.    0.    0.    0.    0.25 -1.5   0.25]
 [ 0.    0.    0.    0.    0.    0.    0.    0.25 -1.5 ]]
B:
 [-40. -25. -25. -25. -25. -25. -25. -25. -35.]
resultado en j: 1 
 [31.01 26.03 25.18 25.03 25.01 25.01 25.08 25.44 27.57]
iteración j: 2
A:
 [[-1.5   0.25  0.    0.    0.    0.    0.    0.    0.  ]
 [ 0.25 -1.5   0.25  0.    0.    0.    0.    0.    0.  ]
 [ 0.    0.25 -1.5   0.25  0.    0.    0.    0.    0.  ]
 [ 0.    0.    0.25 -1.5   0.25  0.    0.    0.    0.  ]
 [ 0.    0.    0.    0.25 -1.5   0.25  0.    0.    0.  ]
 [ 0.    0.    0.    0.    0.25 -1.5   0.25  0.    0.  ]
 [ 0.    0.    0.    0.    0.    0.25 -1.5   0.25  0.  ]
 [ 0.    0.    0.    0.    0.    0.    0.25 -1.5   0.25]
 [ 0.    0.    0.    0.    0.    0.    0.    0.25 -1.5 ]]
B:
 [-46.01 -26.03 -25.18 -25.03 -25.01 -25.01 -25.08 -25.44 -37.57]
resultado en j: 2 
 [35.25 27.49 25.55 25.12 25.03 25.05 25.24 26.07 29.39]
iteración j: 3
A:
 [[-1.5   0.25  0.    0.    0.    0.    0.    0.    0.  ]
 [ 0.25 -1.5   0.25  0.    0.    0.    0.    0.    0.  ]
 [ 0.    0.25 -1.5   0.25  0.    0.    0.    0.    0.  ]
 [ 0.    0.    0.25 -1.5   0.25  0.    0.    0.    0.  ]
 [ 0.    0.    0.    0.25 -1.5   0.25  0.    0.    0.  ]
 [ 0.    0.    0.    0.    0.25 -1.5   0.25  0.    0.  ]
 [ 0.    0.    0.    0.    0.    0.25 -1.5   0.25  0.  ]
 [ 0.    0.    0.    0.    0.    0.    0.25 -1.5   0.25]
 [ 0.    0.    0.    0.    0.    0.    0.    0.25 -1.5 ]]
B:
 [-50.25 -27.49 -25.55 -25.12 -25.03 -25.05 -25.24 -26.07 -39.39]
resultado en j: 3 
 [38.34 29.06 26.09 25.28 25.09 25.13 25.47 26.74 30.72]
EDP Parabólica - Método implícito 
lambda:  0.25
x: [0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
t: [0.   0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 ] ... 1.0
Tabla de resultados en malla EDP Parabólica
j, U[:,: 10 ], primeras iteraciones
10 [60.   47.43 37.58 31.3  27.98 26.64 26.63 27.83 30.43 34.63 40.  ]
9 [60.   46.75 36.68 30.56 27.48 26.3  26.33 27.47 30.04 34.33 40.  ]
8 [60.   45.96 35.69 29.8  27.01 26.   26.06 27.12 29.6  33.99 40.  ]
7 [60.   45.01 34.6  29.02 26.57 25.73 25.81 26.76 29.13 33.58 40.  ]
6 [60.   43.87 33.39 28.24 26.16 25.51 25.58 26.41 28.6  33.09 40.  ]
5 [60.   42.45 32.06 27.48 25.8  25.32 25.39 26.07 28.03 32.48 40.  ]
4 [60.   40.67 30.61 26.75 25.51 25.18 25.24 25.76 27.41 31.71 40.  ]
3 [60.   38.34 29.06 26.09 25.28 25.09 25.13 25.47 26.74 30.72 40.  ]
2 [60.   35.25 27.49 25.55 25.12 25.03 25.05 25.24 26.07 29.39 40.  ]
1 [60.   31.01 26.03 25.18 25.03 25.01 25.01 25.08 25.44 27.57 40.  ]
0 [60. 25. 25. 25. 25. 25. 25. 25. 25. 25. 40.]
>>>

Instrucciones en Python

# EDP parabólicas d2u/dx2  = K du/dt
# método implícito
# Referencia: Chapra 30.3 p.895 pdf.917
#       Rodriguez 10.2.5 p.417
import numpy as np

# INGRESO
# Valores de frontera
Ta = 60
Tb = 40
#T0 = 25 # estado inicial de barra
fx = lambda x: 25 + 0*x # función inicial para T0
a = 0  # longitud en x
b = 1

K = 4     # Constante K
dx = 0.1  # Tamaño de paso
dt = dx/10

n = 100 # iteraciones en tiempo
verdigitos = 2   # decimales a mostrar en tabla de resultados

# PROCEDIMIENTO
# iteraciones en longitud
xi = np.arange(a,b+dx/2,dx)
fi = fx(xi)
m  = len(xi)
ultimox = m-1
ultimot = n-1
# Resultados en tabla u[x,t]
u = np.zeros(shape=(m,n), dtype=float)

# valores iniciales de u[:,j]
j = 0
u[0,:]= Ta
u[1:ultimox,j] = fi[1:ultimox]
u[ultimox,:] = Tb

# factores P,Q,R
lamb = dt/(K*dx**2)
P = lamb
Q = -1 -2*lamb
R = lamb

# Calcula U para cada tiempo + dt
tj = np.arange(0,(n+1)*dt,dt)
j = 1
while not(j>=n):
    # Matriz de ecuaciones
    k = m-2
    A = np.zeros(shape=(k,k), dtype = float)
    B = np.zeros(k, dtype = float)
    for f in range(0,k,1):
        if (f>0):
            A[f,f-1]=P
        A[f,f] = Q
        if (f<(k-1)):
            A[f,f+1]=R
        B[f] = -u[f+1,j-1]
    B[0] = B[0]-P*u[0,j]
    B[k-1] = B[k-1]-R*u[m-1,j]
    # Resuelve sistema de ecuaciones
    C = np.linalg.solve(A, B)

    # copia resultados a u[i,j]
    for f in range(0,k,1):
        u[f+1,j] = C[f]

    # siguiente iteración
    j = j + 1

    # muestra 3 primeras iteraciones
    np.set_printoptions(precision=verdigitos)
    if j<(3+2): 
        print('iteración j:',j-1)
        print('A:\n',A)
        print('B:\n',B)
        print('resultado en j:',j-1,'\n',C)
        
# SALIDA
print('EDP Parabólica - Método implícito ')
print('lambda: ',np.around(lamb,verdigitos))
print('x:',xi)
print('t:',tj[0:len(xi)],'...',tj[-1])
print('Tabla de resultados en malla EDP Parabólica')
print('j, U[:,:',ultimox,'], primeras iteraciones')
for j in range(ultimox,-1,-1):
    print(j,u[:,j])

Para realizar la gráfica se aplica lo mismo que en el método explícito

# GRAFICA ------------
import matplotlib.pyplot as plt
tramos = 10
salto = int(n/tramos) # evita muchas líneas
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.',color='red')
plt.xlabel('x[i]')
plt.ylabel('u[j]')
plt.title('Solución EDP parabólica')
plt.show()

Sin embargo para la gráfica en 3D se ajustan los puntos de referencia agregados por las diferencias finitas.

# GRAFICA en 3D
# vector de tiempo, simplificando en tramos
tramos = 10
salto = int(n/tramos)
if (salto == 0):
    salto = 1
tj = np.arange(0,n*dt,dt)
tk = np.zeros(tramos,dtype=float)

# Extrae parte de la matriz U,acorde a los tramos
U = np.zeros(shape=(tramos,m),dtype=float)
for k in range(0,tramos,1):
    U[k,:] = u[:,k*salto]
    tk[k] = tj[k*salto]
# Malla para cada eje X,Y
Xi, Yi = np.meshgrid(xi,tk)

fig_3D = plt.figure()
graf_3D = fig_3D.add_subplot(111, projection='3d')
graf_3D.plot_wireframe(Xi,Yi,U,
                       color ='blue',label='EDP Parabólica')
graf_3D.plot(Xi[2,0],Yi[2,0],U[2,0],'o',color ='orange')
graf_3D.plot(Xi[2,1],Yi[2,1],U[2,1],'o',color ='salmon')
graf_3D.plot(Xi[2,2],Yi[2,2],U[2,2],'o',color ='salmon')
graf_3D.plot(Xi[1,1],Yi[1,1],U[1,1],'o',color ='green')
graf_3D.set_title('EDP Parabólica')
graf_3D.set_xlabel('x')
graf_3D.set_ylabel('t')
graf_3D.set_zlabel('U')
graf_3D.legend()
graf_3D.view_init(35, -45)
plt.show()

Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada. Revisar los criterios en Chapra 30.2.1 p891, Burden 9Ed 12.2 p727, Rodríguez 10.2.2 p409 .

Tarea o proyecto: Realizar la comparación de tiempos de ejecución entre los métodos explícitos e implícitos. La parte de animación funciona igual en ambos métodos. Los tiempos de ejecución se determinan usando las instrucciones descritas en el enlace: Tiempos de Ejecución en Python

EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]

2017-10-032025-09-07

7.1.1 EDP Parabólicas método explícito con Python

EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]
..

1. Ejercicio

Referencia: Chapra 30.2 p888 pdf912, Burden 9Ed 12.2 p725, Rodríguez 10.2 p406

Siguiendo el tema anterior en EDP Parabólicas, para resolver la parte numérica considere

Valores de frontera: Ta = 60, Tb = 40, T0 = 25
Longitud en x a = 0, b = 1, Constante K= 4
Tamaño de paso dx = 0.1, dt = dx/10

Para la ecuación diferencial parcial parabólica:

\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}

2. Método Explícito

Se usan las diferencias divididas, donde se requieren dos valores para la derivada de orden uno y tres valores para la derivada de orden dos:

\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2}

\frac{\partial u}{\partial t} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}

La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla. La línea de referencia es el tiempo t₀

Luego se sustituyen en la ecuación del problema, obteniendo:

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j+1}-u_{i,j}}{\Delta t}

De la gráfica se destaca que en la fórmula solo hay un valor desconocido, destacado por el punto en amarillo dentro del triángulo. En la ecuación se representa por U[i,j+1].

Despejando la ecuación, se agrupan términos constantes:

λ = \frac{\Delta t}{K (\Delta x)^2}

quedando la ecuación, con los términos ordenados de izquierda a derecha como en la gráfica:

u_{i,j+1} = \lambda u_{i-1,j} +(1-2\lambda)u_{i,j}+\lambda u_{i+1,j}

Al resolver se encuentra que que cada valor en un punto amarillo se calcula como una suma ponderada de valores conocidos, por lo que el desarrollo se conoce como el método explícito.

La ponderación está determinada por los términos P, Q, y R.

\lambda = \frac{\Delta t}{K(\Delta x)^2}

P = \lambda

Q = 1-2\lambda

R = \lambda

u_{i ,j+1} = Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j}

Fórmulas que se desarrollan usando un algoritmo y considerando que al disminuir los valores de Δx y Δt la cantidad de operaciones aumenta.

Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada.

Revisar los criterios en: Chapra 30.2.1 p891 pdf915, Burden 9Ed 12.2 p727, Rodríguez 10.2.2 pdf409 .

\lambda \leq \frac{1}{2}

Cuando λ ≤ 1/2 se tiene como resultado una solución donde los errores no crecen, sino que oscilan.
Haciendo λ ≤ 1/4 asegura que la solución no oscilará.
También se sabe que con λ= 1/6 se tiende a minimizar los errores por truncamiento (véase Carnahan y cols., 1969).

Para resolver la parte numérica considere que:

Valores de frontera: Ta = 60, Tb = 40, Tc = 25 
Longitud en x: a = 0, b = 1 
Constante K = 4 
Tamaño de paso dx = 0.1, dt = dx/10

EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]
..

3. Algoritmo en Python

Se muestra una tabla resumida de resultados a forma de ejemplo.

Método explícito EDP Parabólica
lambda:  0.25
x: [0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]
t: [0.   0.01 0.02 0.03 0.04] ... 1.0
Tabla de resultados en malla EDP Parabólica
j, U[:,: 5 ], primeras iteraciones de  100
5 [60.   44.21 32.93 27.29 25.41 25.05 25.18 25.98 28.4  33.23 40.  ]
4 [60.   42.77 31.29 26.37 25.14 25.   25.06 25.59 27.7  32.62 40.  ]
3 [60.   40.86 29.38 25.55 25.   25.   25.   25.23 26.88 31.8  40.  ]
2 [60.   38.12 27.19 25.   25.   25.   25.   25.   25.94 30.62 40.  ]
1 [60.   33.75 25.   25.   25.   25.   25.   25.   25.   28.75 40.  ]
0 [60. 25. 25. 25. 25. 25. 25. 25. 25. 25. 40.]
>>>

Se presenta la propuesta del algoritmo EDP parabólicas para el método explícito.

# EDP parabólicas d2u/dx2  = K du/dt
# método explícito,usando diferencias divididas
import numpy as np

# INGRESO
# Valores de frontera
Ta = 60  # izquierda de barra
Tb = 40  # derecha de barra
#Tc = 25 # estado inicial de barra en x
fxc = lambda x: 25 + 0*x # f(x) en tiempo inicial

# dimensiones de la barra
a = 0  # longitud en x
b = 1
t0 = 0 # tiempo inicial, aumenta con dt en n iteraciones

K = 4     # Constante K
dx = 0.1  # muestreo en x, tamaño de paso
dt = dx/10

n = 100  # iteraciones en tiempo
verdigitos = 2   # decimales a mostrar en tabla de resultados

# coeficientes de U[x,t]. factores P,Q,R, 
lamb = dt/(K*dx**2)
P = lamb       # izquierda P*U[i-1,j]
Q = 1 - 2*lamb # centro Q*U[i,j]
R = lamb       # derecha R*U[i+1,j]

# PROCEDIMIENTO
# iteraciones en x, longitud
xi = np.arange(a,b+dx/2,dx)
m = len(xi) 
ultimox = m-1
ultimot = n-1

# u[xi,tj], tabla de resultados
u = np.zeros(shape=(m,n+1), dtype=float)

# u[i,j], valores iniciales
u[0,:] = Ta  # Izquierda
u[ultimox,:] = Tb  # derecha
# estado inicial de barra en x, Tc
fic = fxc(xi) # f(x) en tiempo inicial
u[1:ultimox,0] = fic[1:ultimox]

# Calcula U para cada tiempo + dt
tj = np.arange(t0,(n+1)*dt,dt)
for j  in range(0,n,1):
    for i in range(1,ultimox,1):
        # ecuacion discreta, entre [1,ultimox]
        u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j]

# SALIDA
j_mostrar = 5
np.set_printoptions(precision=verdigitos)
print('Método explícito EDP Parabólica')
print('lambda: ',np.around(lamb,verdigitos))
print('x:',xi)
print('t:',tj[0:j_mostrar],'...',tj[-1])
print('Tabla de resultados en malla EDP Parabólica')
print('j, U[:,:',j_mostrar,'], primeras iteraciones de ',n)
for j in range(j_mostrar,-1,-1):
    print(j,u[:,j])

Si la cantidad de puntos aumenta al disminuir Δx y Δt, es mejor disminuir la cantidad de curvas a usar en el gráfico para evitar superponerlas. Se usa el parámetro 'salto' para indicar cada cuántas curvas calculadas se incorporan en la gráfica.

# GRAFICA ------------
import matplotlib.pyplot as plt
tramos = 10
salto = int(n/tramos) # evita muchas líneas
if (salto == 0):
    salto = 1
for j in range(0,n,salto):
    vector = u[:,j]
    plt.plot(xi,vector)
    plt.plot(xi,vector, '.',color='red')
plt.xlabel('x[i]')
plt.ylabel('u[j]')
plt.title('Solución EDP parabólica')
plt.show()

Note que en la gráfica se toma como coordenadas x vs t, mientras que para la solución de la malla en la matriz las se usan filas y columnas. En la matriz el primer índice es fila y el segundo índice es columna.

En el caso de una gráfica que se realice usando los ejes x,t,U en tres dimensiones se requiere usar las instrucciones:

# GRAFICA en 3D ------
tj = np.arange(0,n*dt,dt)
tk = np.zeros(tramos,dtype=float)

# Extrae parte de la matriz U,acorde a los tramos
U = np.zeros(shape=(m,tramos),dtype=float)
for k in range(0,tramos,1):
    U[:,k] = u[:,k*salto]
    tk[k] = tj[k*salto]
# Malla para cada eje X,Y
Xi, Yi = np.meshgrid(xi,tk)
U = np.transpose(U)

fig_3D = plt.figure()
graf_3D = fig_3D.add_subplot(111, projection='3d')
graf_3D.plot_wireframe(Xi,Yi,U, color ='blue')
graf_3D.plot(xi[0],tk[1],U[1,0],'o',color ='orange')
graf_3D.plot(xi[1],tk[1],U[1,1],'o',color ='green')
graf_3D.plot(xi[2],tk[1],U[1,2],'o',color ='green')
graf_3D.plot(xi[1],tk[2],U[2,1],'o',color ='salmon',
             label='U[i,j+1]')
graf_3D.set_title('EDP Parabólica')
graf_3D.set_xlabel('x')
graf_3D.set_ylabel('t')
graf_3D.set_zlabel('U')
graf_3D.legend()
graf_3D.view_init(35, -45)
plt.show()

EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]

Solving the heat equation | DE3. 3Blue1Brown. 16-junio-2019

EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]

2017-10-022025-08-16

7.1 EDP Parabólicas

EDP Parabólica [ concepto ] Método [ explícito ] [ implícito ]
..

1. EDP Parabólicas

Referencia: Chapra 30.2 p.888 pdf.912, Burden 9Ed p714, Rodríguez 10.2 p406

Las Ecuaciones Diferenciales Parciales tipo parabólicas, semejantes a la mostrada, representa la ecuación de calor para una barra aislada sometida a fuentes de calor en cada extremo.

La temperatura se representa en el ejercicio como u[x,t]

\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}

o con vista en 3D:

Para la solución numérica, cambia la ecuación a su forma discreta usando diferencias finitas divididas que se sustituyen en la ecuación,

\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2}

\frac{\partial u}{\partial t} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}

con lo que la ecuación continua se convierte a discreta:

\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j+1}-u_{i,j}}{\Delta t}

Para interpretar mejor el resultado, se usa una malla que en cada nodo representa la temperatura como los valores u[x_i,t_j].

Para simplificar nomenclatura se usan los subíndices i para el eje de las x y j para el eje t, quedando u[ i , j ].

En el enunciado del problema habían establecido los valores en las fronteras:

temperaturas en los extremos Ta, Tb
la temperatura inicial de la barra T0,
El parámetro para la barra K.

El resultado obtenido se interpreta como los valores de temperatura a lo largo de la barra luego de transcurrido un largo tiempo. Las temperaturas en los extremos de la barra varían entre Ta y Tb a lo largo del tiempo.

Tomando como referencia la malla, existirían algunas formas de plantear la solución, dependiendo de la diferencia finita usada: centrada, hacia adelante, hacia atrás.

EDP Parabólica [ concepto ] Método [ explícito ] [ implícito ]

But what is a partial differential equation? | DE2

3Blue1Brown. 2019 Abril 21

Tarea: Revisar ecuación para difusión de gases, segunda ley de Fick.

La difusión molecular desde un punto de vista microscópico y macroscópico.

2017-10-012025-09-12

Unidad 7 EDP - Ecuaciones Diferenciales Parciales

Parabólicas: [ explícito ] [ implícito ]

Elípticas: [ iterativo ] [ implícito ]

Hiperbólicas

2017-09-072025-08-16

6.5 Métodos EDO con gráficos animados en Python

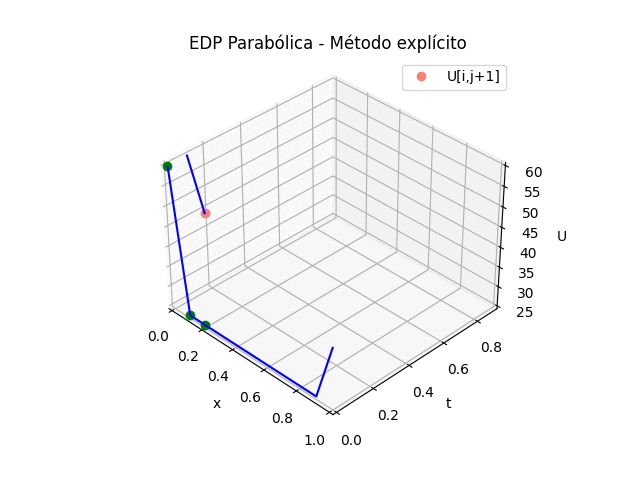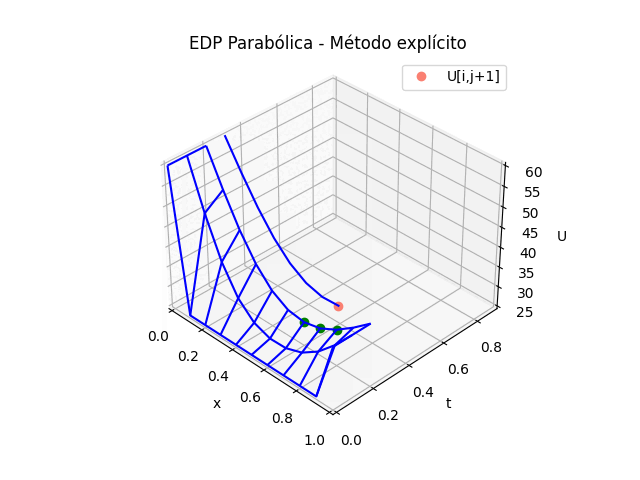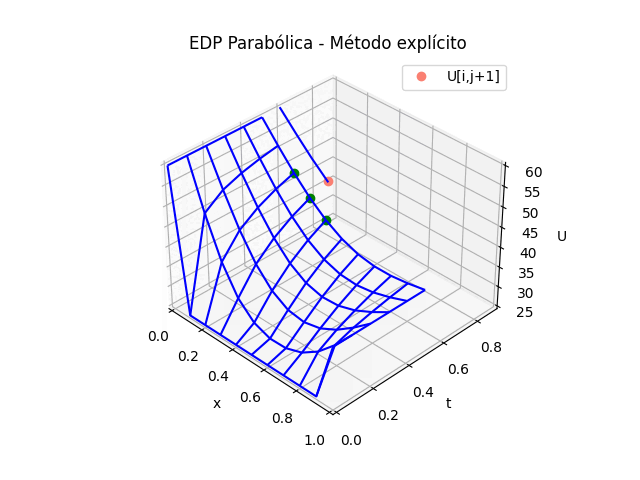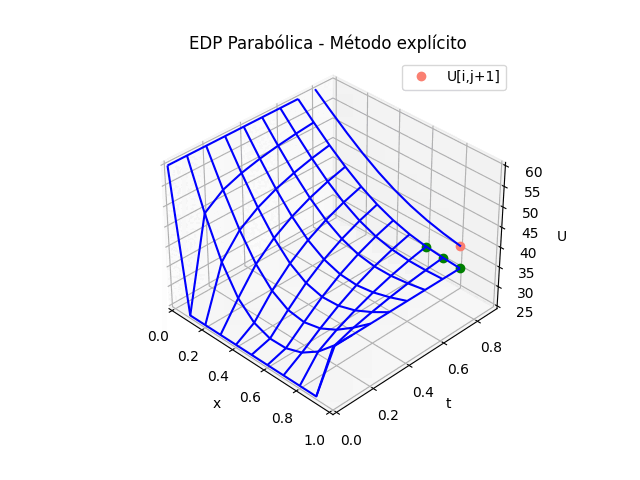
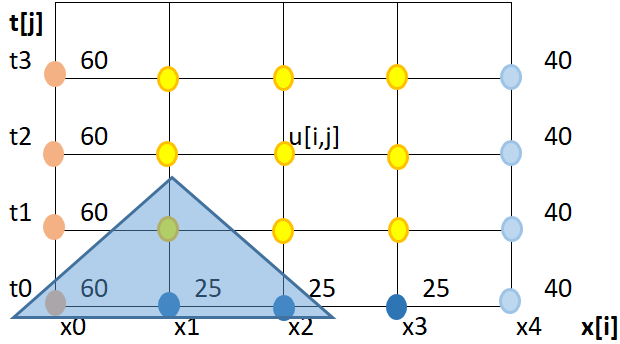
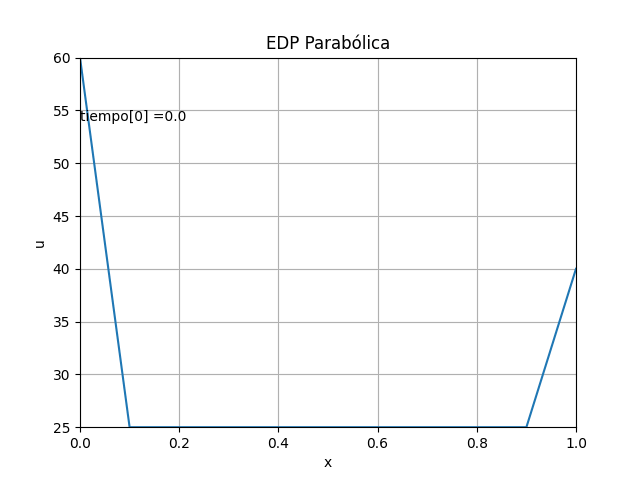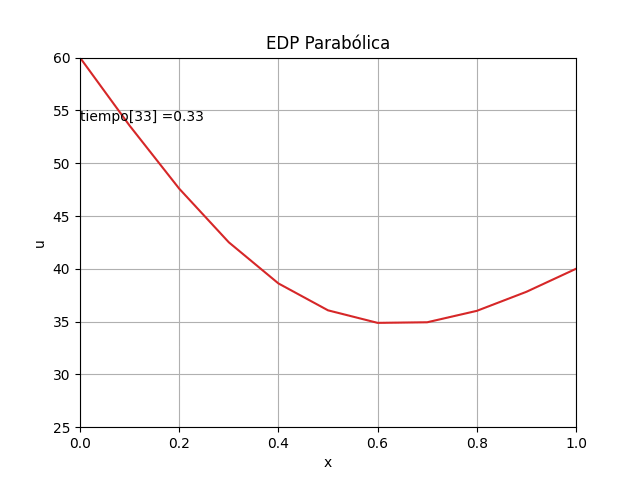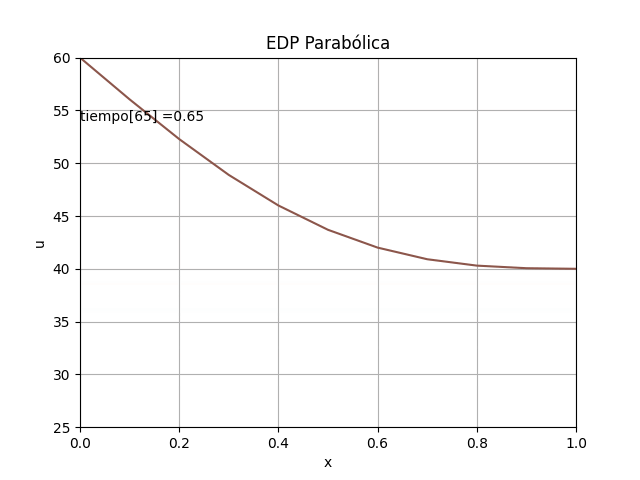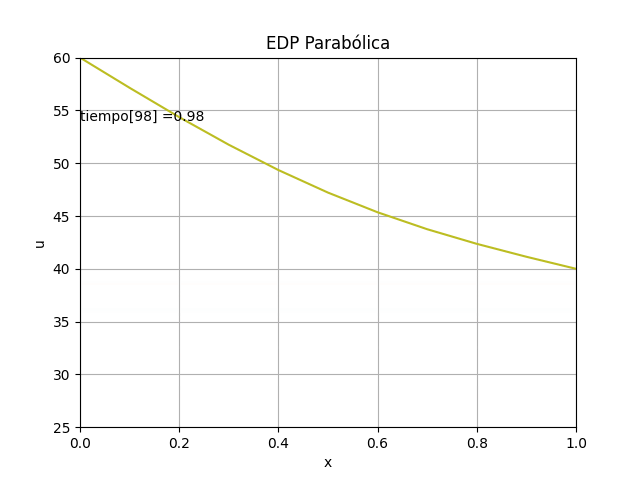
animación: [ EDO Taylor 3t ] [ Runge Kutta dy/dx ] [ Sistemas EDO con RK ]

Solo para fines didácticos, y como complemento para los ejercicios presentados en la unidad para la solución de Ecuaciones Diferenciales Ordinarias, se presentan las instrucciones para las animaciones usadas en la presentación de los conceptos y ejercicios. Los algoritmos para animación NO son necesarios para realizar los ejercicios, que requieren una parte analítica con al menos tres iteraciones en papel y lápiz. Se lo adjunta como una herramienta didáctica de asistencia para las clases.

animación: [ EDO Taylor 3t ] [ Runge Kutta dy/dx ] [ Sistemas EDO con RK ]

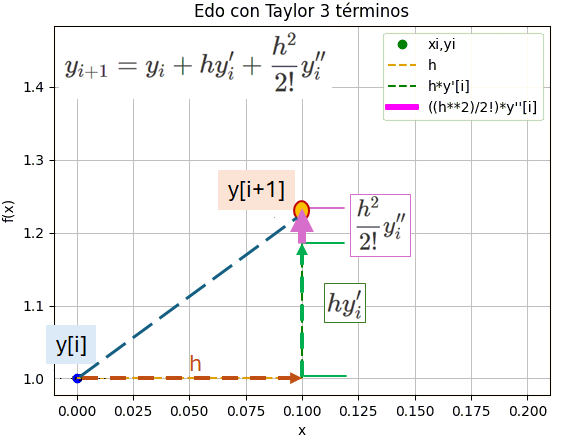
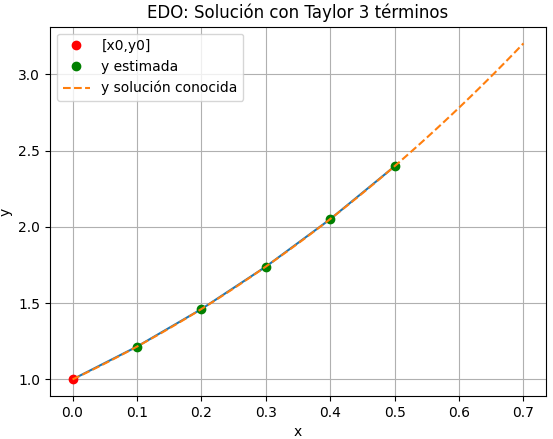
EDO con Taylor de 3 términos

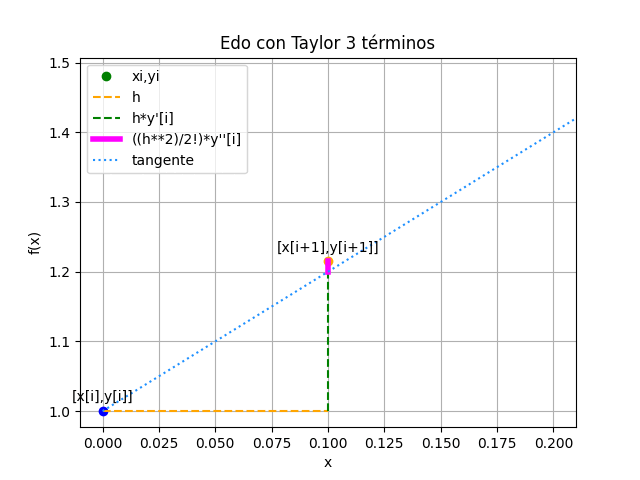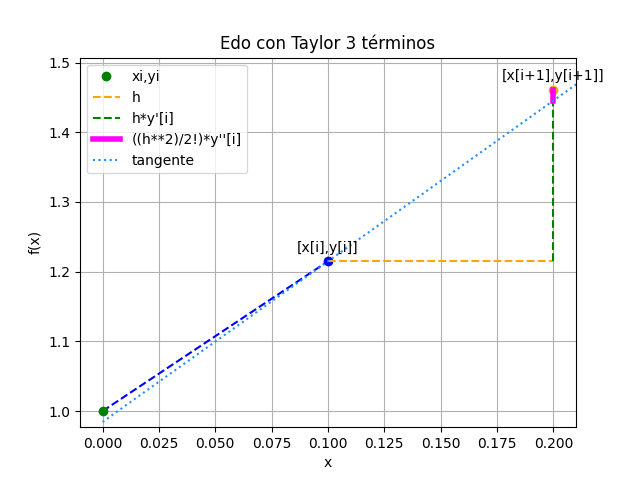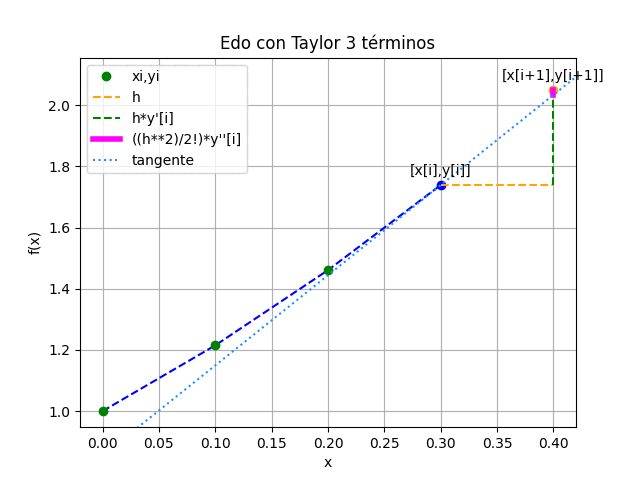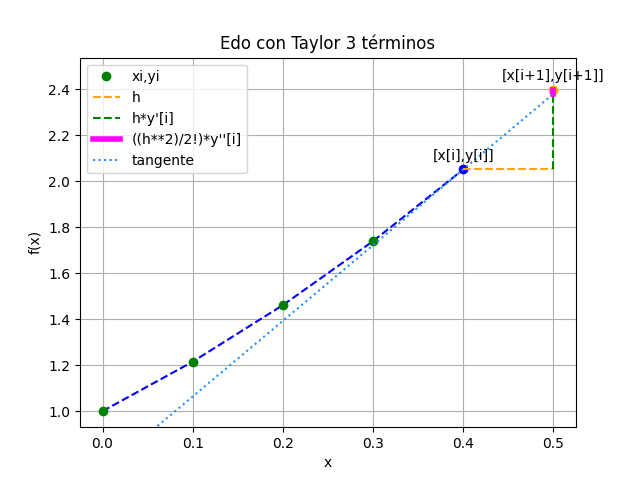
Tabla de resultados:

 EDO con Taylor 3 términos
 [xi,     yi,     d1yi,    d2yi,   término 1,   término 2 ]
[[0.         1.         0.         0.         0.         0.        ]
 [0.1        1.215      2.         3.         0.2        0.015     ]
 [0.2        1.461025   2.305      3.105      0.2305     0.015525  ]
 [0.3        1.73923262 2.621025   3.221025   0.2621025  0.01610513]
 [0.4        2.05090205 2.94923262 3.34923262 0.29492326 0.01674616]
 [0.5        2.39744677 3.29090205 3.49090205 0.32909021 0.01745451]]
>>>

Instrucciones en Python

# EDO. Método de Taylor con3 términos 
# estima solucion para muestras separadas h en eje x
# valores iniciales x0,y0
import numpy as np

def edo_taylor3t(d1y,d2y,x0,y0,h,muestras, vertabla=False, precision=6):
    ''' solucion a EDO usando tres términos de Taylor,
    x0,y0 son valores iniciales, h es el tamaño de paso,
    muestras es la cantidad de puntos a calcular.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,6),dtype=float)
    # incluye el punto [x0,y0]
    tabla[0] = [x0,y0,0,0,0,0]
    x = x0
    y = y0
    for i in range(1,tamano,1):
        d1yi = d1y(x,y)
        d2yi = d2y(x,y)
        y = y + h*d1yi + ((h**2)/2)*d2yi
        x = x + h
        
        term1 = h*d1yi
        term2 = ((h**2)/2)*d2yi
        
        tabla[i] = [x,y,d1yi,d2yi,term1,term2]
    if vertabla==True:
        titulo = ' [xi,     yi,     d1yi,   d2yi,'
        titulo = titulo + '   término 1,   término 2 ]'
        np.set_printoptions(precision)
        print(' EDO con Taylor 3 términos')
        print(titulo)
        print(tabla)
        
    return(tabla)

# PROGRAMA -----------------
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1
# INGRESO.
# d1y = y', d2y = y''
d1y = lambda x,y: y - x**2 + x + 1
d2y = lambda x,y: y - x**2 - x + 2
x0 = 0
y0 = 1
h  = 0.1
muestras = 5

# PROCEDIMIENTO
tabla = edo_taylor3t(d1y,d2y,x0,y0,h,muestras,
                     vertabla=True)

# SALIDA
##print(' EDO con Taylor 3 términos')
##print(' [xi,     yi,     d1yi,',
##      '   d2yi,   término 1,   término 2 ]')
##print(tabla)

# GRAFICA
import matplotlib.pyplot as plt
xi = tabla[:,0]
yi = tabla[:,1]
plt.plot(xi,yi)
plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]')
plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada')
plt.title('EDO: Solución con Taylor 3 términos')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
#plt.show() #comentar para la siguiente gráfica


# GRAFICA CON ANIMACION --------
# import matplotlib.pyplot as plt
import matplotlib.animation as animation

unmetodo = 'Edo con Taylor 3 términos'
narchivo = 'EdoTaylor3t' # nombre archivo GIF
muestras = 51 

# Puntos para la gráfica
a = xi[0]
b = xi[1]
term1 = tabla[:,4]
term2 = tabla[:,5]
dfi = tabla[:,2]
n = len(xi)

# Parametros de trama/foto
retardo = 1000   # milisegundos entre tramas
tramas = len(xi)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
ymax = np.max([yi[0],yi[2]])
ymin = np.min([yi[0],yi[2]])
deltax = np.abs(xi[2]-xi[0])
deltay = np.abs(yi[2]-yi[0])
graf_ani.set_xlim([xi[0],xi[2]+0.05*deltax])
graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.05*deltay])
# Lineas y puntos base
linea_fx, = graf_ani.plot(xi, yi,color='blue',
                          linestyle='dashed')
puntof, = graf_ani.plot(xi[0], yi[0],'o',
                        color='green',
                        label='xi,yi')
puntoa, = graf_ani.plot(xi[0], yi[0],'o',
                        color='Blue')
puntob, = graf_ani.plot(xi[1], yi[1],'o',
                        color='orange')

linea_h, = graf_ani.plot(xi, xi, color='orange',
                         label='h',
                         linestyle='dashed')
linea_term1, = graf_ani.plot(xi, xi,
                             color='green',label="h*y'[i]",
                             linestyle='dashed')
linea_term2, = graf_ani.plot(xi, yi, linewidth=4,
                             color='magenta',
                             label="((h**2)/2!)*y''[i]")
# Aproximacion con tangente
b0 = yi[0] - dfi[1]*xi[0]
tangentei = dfi[1]*xi + b0
linea_tang, = graf_ani.plot(xi, tangentei, color='dodgerblue',
                             label="tangente",
                             linestyle='dotted')

# Cuadros de texto en gráfico
txt_i  = graf_ani.text(xi[0], yi[0]+0.03*deltay,'[x[i],y[i]]',
                       horizontalalignment='center')
txt_i1 = graf_ani.text(xi[1], xi[1]+0.03*deltay,'[x[i+1],y[i+1]]',
                       horizontalalignment='center')
# Configura gráfica
graf_ani.axhline(0, color='black')  # Linea horizontal en cero
graf_ani.set_title(unmetodo)
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Nueva Trama
def unatrama(i,xi,yi,dfi,term1,term2):
    
    if i>1:
        ymax = np.max([yi[0:i+2]])
        ymin = np.min([yi[0:i+2]])
        deltax = np.abs(xi[i+1]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf_ani.set_xlim([xi[0]-0.05*deltax,xi[i+1]+0.05*deltax])
        graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])
    else:
        ymax = np.max([yi[0],yi[2]])
        ymin = np.min([yi[0],yi[2]])
        deltax = np.abs(xi[2]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf_ani.set_xlim([xi[0]-0.05*deltax,xi[2]+0.05*deltax])
        graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])
    # actualiza cada punto
    puntoa.set_xdata([xi[i]]) 
    puntoa.set_ydata([yi[i]])
    puntob.set_xdata([xi[i+1]]) 
    puntob.set_ydata([yi[i+1]])
    puntof.set_xdata([xi[0:i]]) 
    puntof.set_ydata([yi[0:i]])
    # actualiza cada linea
    linea_fx.set_xdata(xi[0:i+1])
    linea_fx.set_ydata(yi[0:i+1])
    linea_h.set_xdata([xi[i],xi[i+1]])
    linea_h.set_ydata([yi[i],yi[i]])
    linea_term1.set_xdata([xi[i+1],xi[i+1]])
    linea_term1.set_ydata([yi[i],yi[i]+term1[i+1]])
    linea_term2.set_xdata([xi[i+1],xi[i+1]])
    linea_term2.set_ydata([yi[i]+term1[i+1],
                           yi[i]+term1[i+1]+term2[i+1]])
    
    b0 = yi[i] - dfi[i+1]*xi[i]
    tangentei = dfi[i+1]*xi + b0
    linea_tang.set_ydata(tangentei)
    # actualiza texto
    txt_i.set_position([xi[i], yi[i]+0.03*deltay])
    txt_i1.set_position([xi[i+1], yi[i+1]+0.03*deltay])

    return (puntoa,puntob,puntof,
            linea_fx,linea_h,linea_tang,
            linea_term1,linea_term2,
            txt_i,txt_i1,)
# Limpia Trama anterior
def limpiatrama(): 
    puntoa.set_ydata(np.ma.array(xi, mask=True))
    puntob.set_ydata(np.ma.array(xi, mask=True))
    puntof.set_ydata(np.ma.array(xi, mask=True))
    linea_h.set_ydata(np.ma.array(xi, mask=True))
    linea_term1.set_ydata(np.ma.array(xi, mask=True))
    linea_term2.set_ydata(np.ma.array(xi, mask=True))
    linea_tang.set_ydata(np.ma.array(xi, mask=True))
    return (puntoa,puntob,puntof,
            linea_fx,linea_h,linea_tang,
            linea_term1,linea_term2,
            txt_i,txt_i1,)

# Trama contador
i = np.arange(0,tramas-1,1)
ani = animation.FuncAnimation(fig_ani,
                              unatrama,
                              i ,
                              fargs = (xi,yi,dfi,term1,term2),
                              init_func = limpiatrama,
                              interval = retardo,
                              blit=False)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_GIFanimado.gif', writer='imagemagick')
# ani.save(narchivo+'_video.mp4')
plt.draw()
plt.show()

animación: [ EDO Taylor 3t ] [ Runge Kutta dy/dx ] [ Sistemas EDO con RK ]

Runge Kutta de 2do Orden para primera derivada

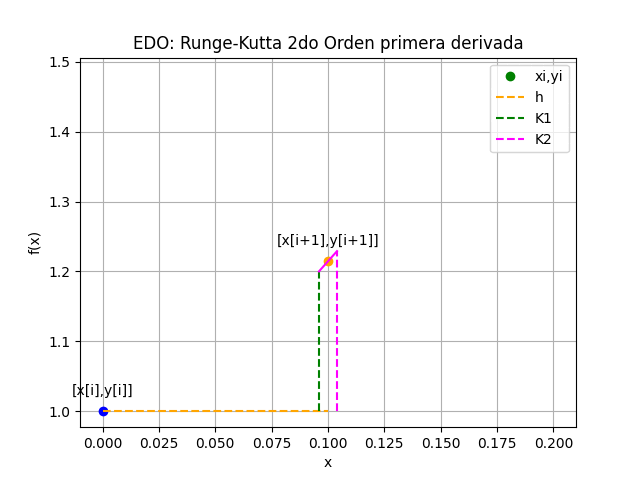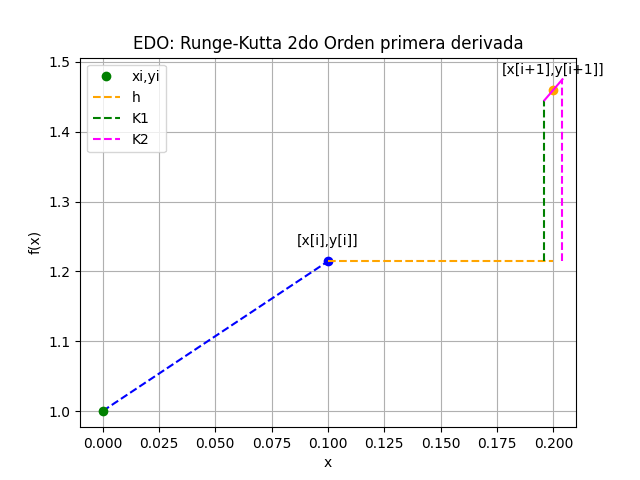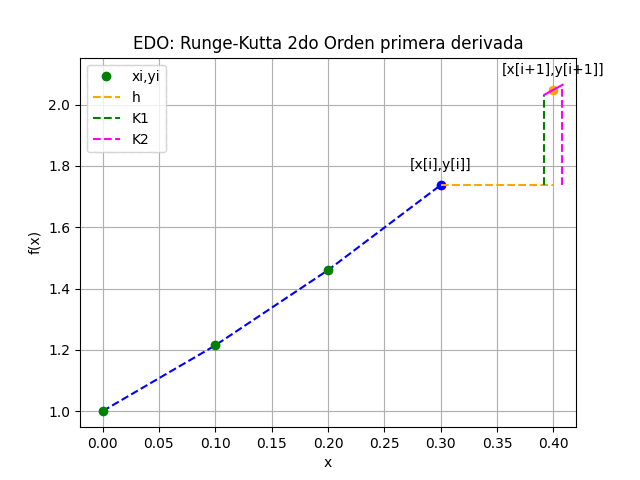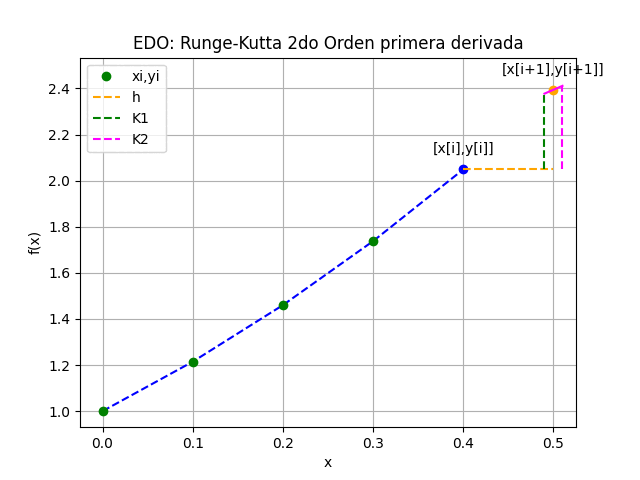
 EDO con Runge-Kutta 2do Orden primera derivada
 [xi,     yi,     K1,    K2 ]
[[0.       1.       0.       0.      ]
 [0.1      1.2145   0.2      0.229   ]
 [0.2      1.459973 0.23045  0.260495]
 [0.3      1.73757  0.261997 0.293197]
 [0.4      2.048564 0.294757 0.327233]
 [0.5      2.394364 0.328856 0.362742]]

Instrucciones en Python

# EDO. Método de Runge-Kutta 2do Orden primera derivada 
# estima solucion para muestras separadas h en eje x
# valores iniciales x0,y0
import numpy as np

def rungekutta2(d1y,x0,y0,h,muestras, vertabla=False, precision=6):
    ''' solucion a EDO con Runge-Kutta 2do Orden primera derivada,
        x0,y0 son valores iniciales
        muestras es la cantidad de puntos a calcular con tamaño de paso h.
    '''
    # Runge Kutta de 2do orden
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,2+2),dtype=float)
    
    # incluye el punto [x0,y0]
    tabla[0] = [x0,y0,0,0]
    xi = x0
    yi = y0
    for i in range(1,tamano,1):
        K1 = h * d1y(xi,yi)
        K2 = h * d1y(xi+h, yi + K1)

        yi = yi + (1/2)*(K1+K2)
        xi = xi + h
        
        tabla[i] = [xi,yi,K1,K2]
    if vertabla==True:
        np.set_printoptions(precision)
        titulo = ' [xi,     yi,     K1,    K2 ]'
        print(' EDO con Runge-Kutta 2do Orden primera derivada')
        print(titulo)
        print(tabla)
    return(tabla)

# PROGRAMA -----------------
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1
# INGRESO.
# d1y = y', d2y = y''
d1y = lambda x,y: y - x**2 + x + 1
d2y = lambda x,y: y - x**2 - x + 2
x0 = 0
y0 = 1
h  = 0.1
muestras = 5

# PROCEDIMIENTO
tabla = rungekutta2(d1y,x0,y0,h,muestras,
                     vertabla=True)

# SALIDA
##print(' EDO con Runge-Kutta 2do Orden primera derivada')
##print(' [xi,     yi,     d1yi,',', K1,   K2 ]')
##print(tabla)

# GRAFICA
import matplotlib.pyplot as plt
xi = tabla[:,0]
yi = tabla[:,1]
plt.plot(xi,yi)
plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]')
plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada')
plt.title('EDO: Solución Runge-Kutta 2do Orden primera derivada')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
#plt.show() #comentar para la siguiente gráfica


# GRAFICA CON ANIMACION --------
# import matplotlib.pyplot as plt
import matplotlib.animation as animation

unmetodo = 'EDO: Runge-Kutta 2do Orden primera derivada'
narchivo = 'EdoRK2df' # nombre archivo GIF
muestras = 51 

# Puntos para la gráfica
a = xi[0]
b = xi[1]
K1 = tabla[:,2]
K2 = tabla[:,3]
n = len(xi)

# Parametros de trama/foto
retardo = 1000   # milisegundos entre tramas
tramas = len(xi)

# GRAFICA animada en fig_ani
fig_ani, graf_ani = plt.subplots()
ymax = np.max([yi[0],yi[2]])
ymin = np.min([yi[0],yi[2]])
deltax = np.abs(xi[2]-xi[0])
deltay = np.abs(yi[2]-yi[0])
graf_ani.set_xlim([xi[0]-0.05*deltax,xi[2]+0.05*deltax])
graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])
# Lineas y puntos base
linea_fx, = graf_ani.plot(xi, yi,color='blue',
                          linestyle='dashed')
puntof, = graf_ani.plot(xi[0], yi[0],'o',
                        color='green',
                        label='xi,yi')
puntoa, = graf_ani.plot(xi[0], yi[0],'o',
                        color='Blue')
puntob, = graf_ani.plot(xi[1], yi[1],'o',
                        color='orange')

linea_h, = graf_ani.plot(xi, xi, color='orange',
                         label='h',
                         linestyle='dashed')
linea_K1, = graf_ani.plot(xi-0.02*deltax, xi-0.02*deltax,
                          color='green',label="K1",
                          linestyle='dashed')
linea_K2, = graf_ani.plot(xi+0.02*deltax, yi,
                          color='magenta',
                          label="K2",
                          linestyle='dashed')
linea_K12, = graf_ani.plot(xi, yi,
                          color='magenta')

# Cuadros de texto en gráfico
txt_i  = graf_ani.text(xi[0], yi[0]+0.05*deltay,'[x[i],y[i]]',
                       horizontalalignment='center')
txt_i1 = graf_ani.text(xi[1], xi[1]+0.05*deltay,'[x[i+1],y[i+1]]',
                       horizontalalignment='center')

# Configura gráfica
graf_ani.axhline(0, color='black')  # Linea horizontal en cero
graf_ani.set_title(unmetodo)
graf_ani.set_xlabel('x')
graf_ani.set_ylabel('f(x)')
graf_ani.legend()
graf_ani.grid()

# Nueva Trama
def unatrama(i,xi,yi,term1,term2):   
    if i>1:
        ymax = np.max([yi[0:i+2]])
        ymin = np.min([yi[0:i+2]])
        deltax = np.abs(xi[i+1]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf_ani.set_xlim([xi[0]-0.05*deltax,xi[i+1]+0.05*deltax])
        graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])
    else:
        ymax = np.max([yi[0],yi[2]])
        ymin = np.min([yi[0],yi[2]])
        deltax = np.abs(xi[2]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf_ani.set_xlim([xi[0]-0.05*deltax,xi[2]+0.05*deltax])
        graf_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])
    # actualiza cada punto
    puntoa.set_xdata([xi[i]]) 
    puntoa.set_ydata([yi[i]])
    puntob.set_xdata([xi[i+1]]) 
    puntob.set_ydata([yi[i+1]])
    puntof.set_xdata(xi[0:i]) 
    puntof.set_ydata(yi[0:i])
    # actualiza cada linea
    linea_fx.set_xdata(xi[0:i+1])
    linea_fx.set_ydata(yi[0:i+1])
    linea_h.set_xdata([xi[i],xi[i+1]])
    linea_h.set_ydata([yi[i],yi[i]])
    linea_K1.set_xdata([xi[i+1]-0.02*deltax,xi[i+1]-0.02*deltax])
    linea_K1.set_ydata([yi[i],yi[i]+K1[i+1]])
    linea_K2.set_xdata([xi[i+1]+0.02*deltax,xi[i+1]+0.02*deltax])
    linea_K2.set_ydata([yi[i],yi[i]+K2[i+1]])
    linea_K12.set_xdata([xi[i+1]-0.02*deltax,xi[i+1]+0.02*deltax])
    linea_K12.set_ydata([yi[i]+K1[i+1],yi[i]+K2[i+1]])
    # actualiza texto
    txt_i.set_position([xi[i], yi[i]+0.05*deltay])
    txt_i1.set_position([xi[i+1], yi[i+1]+0.05*deltay])

    return (puntoa,puntob,puntof,
            linea_fx,linea_h,linea_K1,linea_K2,linea_K12,
            txt_i,txt_i1,)
# Limpia Trama anterior
def limpiatrama(): 
    puntoa.set_ydata(np.ma.array(xi, mask=True))
    puntob.set_ydata(np.ma.array(xi, mask=True))
    puntof.set_ydata(np.ma.array(xi, mask=True))
    linea_h.set_ydata(np.ma.array(xi, mask=True))
    linea_K1.set_ydata(np.ma.array(xi, mask=True))
    linea_K2.set_ydata(np.ma.array(xi, mask=True))
    linea_K12.set_ydata(np.ma.array(xi, mask=True))
    
    return (puntoa,puntob,puntof,
            linea_fx,linea_h,linea_K1,linea_K2,linea_K12,
            txt_i,txt_i1,)

# Trama contador
i = np.arange(0,tramas-1,1)
ani = animation.FuncAnimation(fig_ani,
                              unatrama,
                              i ,
                              fargs = (xi,yi,K1,K2),
                              init_func = limpiatrama,
                              interval = retardo,
                              blit=False)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_GIFanimado.gif', writer='imagemagick')
# ani.save(narchivo+'_video.mp4')
plt.draw()
plt.show()

animación: [ EDO Taylor 3t ] [ Runge Kutta dy/dx ] [ Sistemas EDO con RK ]
..

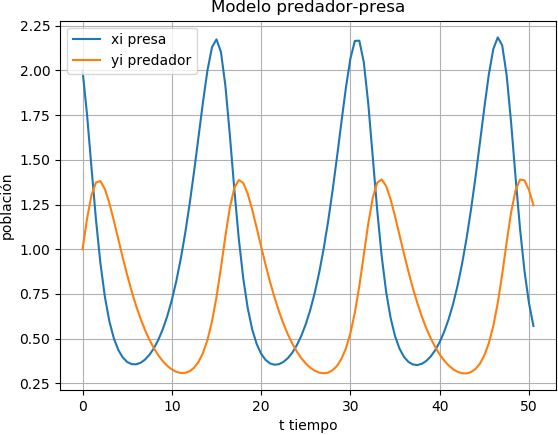
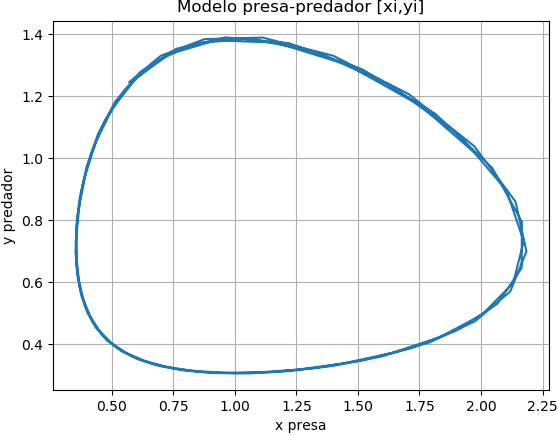
Sistemas EDO. modelo depredador-presa con Runge-Kutta 2do Orden
.

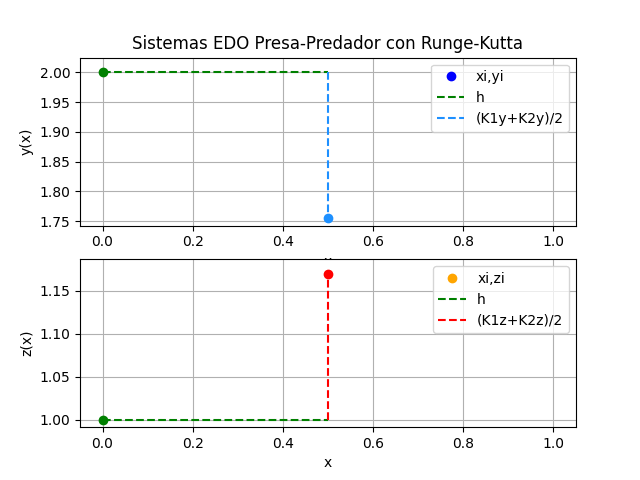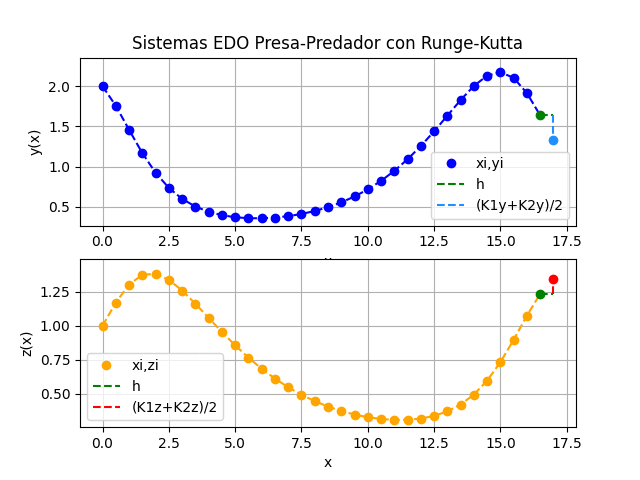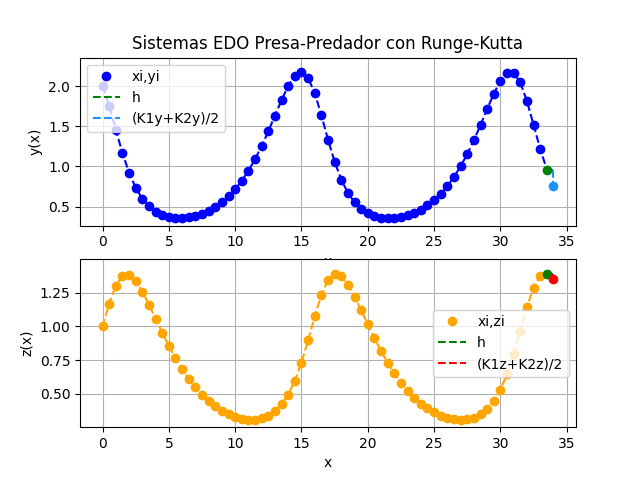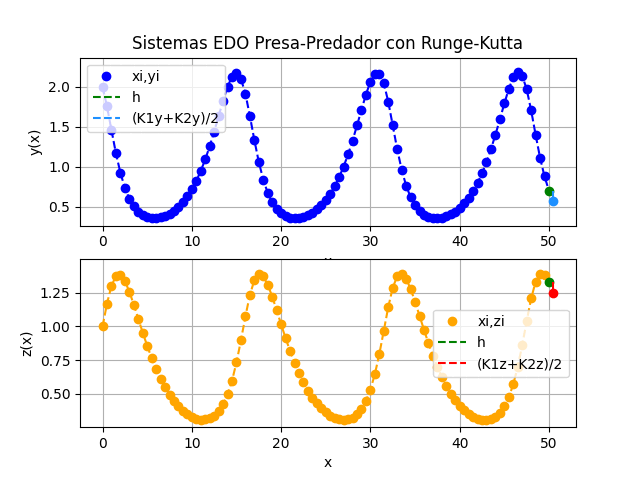
Instrucciones en Python

# Modelo predador-presa de Lotka-Volterra
# Sistemas EDO con Runge Kutta de 2do Orden
import numpy as np

def rungekutta2_fg(f,g,x0,y0,z0,h,muestras,
                   vertabla=False, precision = 6):
    ''' solucion a EDO con Runge-Kutta 2do Orden Segunda derivada,
        x0,y0 son valores iniciales, h es tamano de paso,
        muestras es la cantidad de puntos a calcular.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,3+4),dtype=float)

    # incluye el punto [x0,y0,z0]
    tabla[0] = [x0,y0,z0,0,0,0,0]
    xi = x0
    yi = y0
    zi = z0
    i=0
    if vertabla==True:
        print('Runge-Kutta Segunda derivada')
        print('i ','[ xi,  yi,  zi',']')
        print('   [ K1y,  K1z,  K2y,  K2z ]')
        np.set_printoptions(precision)
        print(i,tabla[i,0:3])
        print('  ',tabla[i,3:])
    for i in range(1,tamano,1):
        K1y = h * f(xi,yi,zi)
        K1z = h * g(xi,yi,zi)
        
        K2y = h * f(xi+h, yi + K1y, zi + K1z)
        K2z = h * g(xi+h, yi + K1y, zi + K1z)

        yi = yi + (K1y+K2y)/2
        zi = zi + (K1z+K2z)/2
        xi = xi + h
        
        tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z]
        if vertabla==True:
            txt = ' '
            if i>=10:
                txt='  '
            print(str(i)+'',tabla[i,0:3])
            print(txt,tabla[i,3:])
    return(tabla)

# PROGRAMA ------------------

# INGRESO
# Parámetros de las ecuaciones
a = 0.5
b = 0.7
c = 0.35
d = 0.35

# Ecuaciones
f = lambda t,x,y : a*x -b*x*y
g = lambda t,x,y : -c*y + d*x*y

# Condiciones iniciales
t0 = 0
x0 = 2
y0 = 1

# parámetros del algoritmo
h = 0.5
muestras = 101

# PROCEDIMIENTO
tabla = rungekutta2_fg(f,g,t0,x0,y0,h,muestras,vertabla=True)
ti = tabla[:,0]
xi = tabla[:,1]
yi = tabla[:,2]

# SALIDA
print('Sistemas EDO: Modelo presa-predador')
##np.set_printoptions(precision=6)
##print(' [ ti, xi, yi]')
##print(tabla[:,0:4])

# GRAFICA tiempos vs población
import matplotlib.pyplot as plt

fig_t, (graf1,graf2) = plt.subplots(2)
fig_t.suptitle('Modelo predador-presa')
graf1.plot(ti,xi, color='blue',label='xi presa')

#graf1.set_xlabel('t tiempo')
graf1.set_ylabel('población x')
graf1.legend()
graf1.grid()

graf2.plot(ti,yi, color='orange',label='yi predador')
graf2.set_xlabel('t tiempo')
graf2.set_ylabel('población y')
graf2.legend()
graf2.grid()

# gráfica xi vs yi
fig_xy, graf3 = plt.subplots()
graf3.plot(xi,yi)

graf3.set_title('Modelo presa-predador [xi,yi]')
graf3.set_xlabel('x presa')
graf3.set_ylabel('y predador')
graf3.grid()
#plt.show()


# GRAFICA CON ANIMACION --------
# import matplotlib.pyplot as plt
import matplotlib.animation as animation
xi = tabla[:,0]
yi = tabla[:,1]
zi = tabla[:,2]

unmetodo = 'Sistemas EDO Presa-Predador con Runge-Kutta'
narchivo = 'EdoPresaPredador' # nombre archivo GIF
muestras = 51 

# Puntos para la gráfica
a = xi[0]
b = xi[1]
n = len(ti)

# Parametros de trama/foto
retardo = 1000   # milisegundos entre tramas
tramas = len(xi)

# GRAFICA animada en fig_ani
fig_ani, (graf1_ani,graf2_ani) = plt.subplots(2)
ymax = np.max([yi[0],yi[2]])
ymin = np.min([yi[0],yi[2]])
deltax = np.abs(xi[2]-xi[0])
deltay = np.abs(yi[2]-yi[0])
graf1_ani.set_xlim([xi[0],xi[2]+0.05*deltax])
graf1_ani.set_ylim([ymin-0.05*deltay,ymax+0.05*deltay])

zmax = np.max([zi[0],zi[2]])
zmin = np.min([zi[0],zi[2]])
deltax = np.abs(xi[2]-xi[0])
deltaz = np.abs(zi[2]-zi[0])
graf2_ani.set_xlim([xi[0],xi[2]+0.05*deltax])
graf2_ani.set_ylim([zmin-0.05*deltaz,zmax+0.05*deltaz])
# Lineas y puntos base
linea_fx, = graf1_ani.plot(xi, yi,color='blue',
                          linestyle='dashed')
puntof, = graf1_ani.plot(xi[0], yi[0],'o',
                        color='blue',
                        label='xi,yi')
puntoa, = graf1_ani.plot(xi[0], yi[0],'o',
                        color='green')
puntob, = graf1_ani.plot(xi[1], yi[1],'o',
                        color='dodgerblue')
linea_h, = graf1_ani.plot(xi, xi, color='green',
                         label='h',
                         linestyle='dashed')
linea_term1, = graf1_ani.plot(xi, xi,
                             color='dodgerblue',label="(K1y+K2y)/2",
                             linestyle='dashed')
# Cuadros de texto en gráfico
#txt_i  = graf1_ani.text(xi[0], yi[0]+0.03*deltay,'[x[i],y[i]]',
#                       horizontalalignment='center')
#txt_i1 = graf1_ani.text(xi[1], xi[1]+0.03*deltay,'[x[i+1],y[i+1]]',
#                       horizontalalignment='center')

linea_gx, = graf2_ani.plot(xi, zi,color='orange',
                          linestyle='dashed')
puntog, = graf2_ani.plot(xi[0], zi[0],'o',
                        color='orange',
                        label='xi,zi')
puntog_a, = graf2_ani.plot(xi[0], zi[0],'o',
                        color='green')
puntog_b, = graf2_ani.plot(xi[1], zi[1],'o',
                        color='red')
lineag_h, = graf2_ani.plot(xi, xi, color='green',
                         label='h',
                         linestyle='dashed')
lineag_term1, = graf2_ani.plot(xi, xi,
                             color='red',label="(K1z+K2z)/2",
                             linestyle='dashed')

# Configura gráfica
graf1_ani.axhline(0, color='black')  # Linea horizontal en cero
graf1_ani.set_title(unmetodo)
graf1_ani.set_xlabel('x')
graf1_ani.set_ylabel('y(x)')
graf1_ani.legend()
graf1_ani.grid()

graf2_ani.axhline(0, color='black')  # Linea horizontal en cero
#graf2_ani.set_title(unmetodo)
graf2_ani.set_xlabel('x')
graf2_ani.set_ylabel('z(x)')
graf2_ani.legend()
graf2_ani.grid()

# Nueva Trama
def unatrama(i,xi,yi,zi):
    
    if i>1:
        ymax = np.max([yi[0:i+2]])
        ymin = np.min([yi[0:i+2]])
        deltax = np.abs(xi[i+1]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf1_ani.set_xlim([xi[0]-0.05*deltax,xi[i+1]+0.05*deltax])
        graf1_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])

        zmax = np.max([zi[0:i+2]])
        zmin = np.min([zi[0:i+2]])
        deltaz = np.abs(zmax-zmin)
        graf2_ani.set_xlim([xi[0]-0.05*deltax,xi[i+1]+0.05*deltax])
        graf2_ani.set_ylim([zmin-0.05*deltaz,zmax+0.1*deltaz])
    else:
        ymax = np.max([yi[0:2]])
        ymin = np.min([yi[0:2]])
        deltax = np.abs(xi[2]-xi[0])
        deltay = np.abs(ymax-ymin)
        graf1_ani.set_xlim([xi[0]-0.05*deltax,xi[2]+0.05*deltax])
        graf1_ani.set_ylim([ymin-0.05*deltay,ymax+0.1*deltay])

        zmax = np.max([zi[0:2]])
        zmin = np.min([zi[0:2]])
        deltaz = np.abs(zmax-zmin)
        graf2_ani.set_xlim([xi[0]-0.05*deltax,xi[2]+0.05*deltax])
        graf2_ani.set_ylim([zmin-0.05*deltaz,zmax+0.1*deltaz])
    # actualiza cada punto
    puntoa.set_xdata([xi[i]]) 
    puntoa.set_ydata([yi[i]])
    puntob.set_xdata([xi[i+1]]) 
    puntob.set_ydata([yi[i+1]])
    puntof.set_xdata(xi[0:i]) 
    puntof.set_ydata(yi[0:i])
    # actualiza cada linea
    linea_fx.set_xdata(xi[0:i+1])
    linea_fx.set_ydata(yi[0:i+1])
    linea_h.set_xdata([xi[i],xi[i+1]])
    linea_h.set_ydata([yi[i],yi[i]])
    linea_term1.set_xdata([xi[i+1],xi[i+1]])
    linea_term1.set_ydata([yi[i],yi[i+1]])
    # actualiza texto
    #txt_i.set_position([xi[i], yi[i]+0.03*deltay])
    #txt_i1.set_position([xi[i+1], yi[i+1]+0.03*deltay])

    # actualiza cada punto
    puntog_a.set_xdata([xi[i]]) 
    puntog_a.set_ydata([zi[i]])
    puntog_b.set_xdata([xi[i+1]]) 
    puntog_b.set_ydata([zi[i+1]])
    puntog.set_xdata(xi[0:i]) 
    puntog.set_ydata(zi[0:i])
    # actualiza cada linea
    linea_gx.set_xdata(xi[0:i+1])
    linea_gx.set_ydata(zi[0:i+1])
    lineag_h.set_xdata([xi[i],xi[i+1]])
    lineag_h.set_ydata([zi[i],zi[i]])
    lineag_term1.set_xdata([xi[i+1],xi[i+1]])
    lineag_term1.set_ydata([zi[i],zi[i+1]])

    return (puntoa,puntob,puntof,
            linea_fx,linea_h,
            linea_term1,)
            #txt_i,txt_i1,)
# Limpia Trama anterior
def limpiatrama(): 
    puntoa.set_ydata(np.ma.array(xi, mask=True))
    puntob.set_ydata(np.ma.array(xi, mask=True))
    puntof.set_ydata(np.ma.array(xi, mask=True))
    linea_h.set_ydata(np.ma.array(xi, mask=True))
    linea_term1.set_ydata(np.ma.array(xi, mask=True))

    puntog_a.set_ydata(np.ma.array(xi, mask=True))
    puntog_b.set_ydata(np.ma.array(xi, mask=True))
    puntog.set_ydata(np.ma.array(xi, mask=True))
    lineag_h.set_ydata(np.ma.array(xi, mask=True))
    lineag_term1.set_ydata(np.ma.array(xi, mask=True))
    return (puntoa,puntob,puntof,
            linea_fx,linea_h,
            linea_term1,
            puntog_a,puntog_b,puntog,
            linea_gx,lineag_h,
            lineag_term1,)
            #txt_i,txt_i1,)

# Trama contador
i = np.arange(0,tramas-1,1)
ani = animation.FuncAnimation(fig_ani,
                              unatrama,
                              i ,
                              fargs = (xi,yi,zi),
                              init_func = limpiatrama,
                              interval = retardo,
                              blit=False)
# Graba Archivo GIFAnimado y video
ani.save(narchivo+'_GIFanimado.gif', writer='imagemagick')
# ani.save(narchivo+'_video.mp4')
plt.draw()
plt.show()

animación: [ EDO Taylor 3t ] [ Runge Kutta dy/dx ] [ Sistemas EDO con RK ]

2017-09-062025-08-16

6.4 Sistemas EDO. modelo depredador-presa con Runge-Kutta y Python

Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ]
..

1. Ejercicio

Referencia: Chapra 28.2 p831 pdf855, Rodríguez 9.2.1 p263
https://es.wikipedia.org/wiki/Ecuaciones_Lotka%E2%80%93Volterra
https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations

Modelos depredador-presa y caos. Ecuaciones Lotka-Volterra. En el sistema de ecuaciones:

\frac{dx}{dt} = ax - bxy

\frac{dy}{dt} = -cy + dxy

variables
x = número de presas
y = número de depredadores
t = tiempo de observación
coeficientes
a = razón de crecimiento de la presa, (0.5)
c = razón de muerte del depredador (0.35)
b = efecto de la interacción depredador-presa sobre la muerte de la presa (0.7)
d = efecto de la interacción depredador-presa sobre el crecimiento del depredador, (0.35)

Considere como puntos iniciales en la observación de las especies:
t = 0, x = 2, y = 1, h = 0.5

Los términos que multiplican xy hacen que las ecuaciones sean no lineales.
Observe que la variable tiempo no se encuentra en las expresiones f y g, h se aplica a tiempo.

Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ]
..

2. Desarrollo analítico

Para resolver el sistema, se plantean las ecuaciones de forma simplificada para el algoritmo:

f(t,x,y) = 0.5 x - 0.7 xy

g(t,x,y) = -0.35y + 0.35xy

Las expresiones se adaptan al método de Runge-Kutta para primeras derivadas por cada variable de población. Se deben usar de forma simultánea para cada tiempo t.

K1x = h f(t,x,y) = 0.5 \Big( 0.5 x - 0.7 xy \Big)

K1y = h g(t,x,y) = 0.5 \Big(-0.35y + 0.35xy \Big)

K2x = h f(t+h,x+K1x,y+K1y)

= 0.5 \Big( 0.5 (x+K1x) - 0.7 (x+K1x)(y+K1y) \Big)

K2y = h g(t+h,x+K1x,y+K1y)

= 0.5 \Big(-0.35(y+K1y) + 0.35(x+K1x)(y+K1y) \Big)

x[i+1] = x[i] + \frac{K1x+K2x}{2}

y[i+1] = y[i] + \frac{K1y+K2y}{2}

t[i+1] = t[i] + h

con lo que se puede aplicar al ejercicio en cada iteración. dadas las condiciones iniciales.

itera = 0

t = 0, x = 2, y = 1, h = 0.5

K1x = 0.5 f(0,2,1) = 0.5 \Big( 0.5 (2) - 0.7 (2)(1) \Big) = -0.2

K1y = 0.5 g(0,2,1) = 0.5 \Big(-0.35(1) + 0.35(2)(1) \Big) =0.175

K2x = 0.5 f(0+0.5, 2+(-0.2), 1+0.175)

= 0.5 \Big( 0.5 (2+(-0.2)) - 0.7 (2+(-0.2))(1+0.175) \Big)

= -0.29025

K2y = 0.5 g(0+0.5, 2+(-0.2), 1+0.175)

= 0.5 \Big(-0.35(1+0.175) + 0.35(2+(-0.2))(1+0.175) \Big)

= 0.1645

x[1] = x[0] + \frac{K1x+K2x}{2} = 2 + \frac{-0.2+(-0.29025)}{2} = 1.7548

y[1] = y[0] + \frac{K1y+K2y}{2} = 1 + \frac{0.175+0.1645}{2}= 1.1697

t[1] = t[0] + h = 0 +0.5 = 0.5

itera = 1

t = 0.5, x = 1.7548, y = 1.1697, h = 0.5

K1x = 0.5 \Big( 0.5 (0,1.7548) - 0.7 (0,1.7548)(1.1697) \Big) = -0.2797

K1y = 0.5 \Big(-0.35(1.1697) + 0.35(1.7548)(1.1697) \Big) =0.1545

K2x = 0.5 \Big( 0.5 (1.7548+(-0.2797)) - 0.7 (1.7548+(-0.2797))(1.1697+0.1545) \Big)

=-0.3149

K2y = 0.5 \Big(-0.35(1.1697+0.1545) + 0.35(1.7548+(-0.2797))(1.1697+0.1545) \Big)

= 0.1645

x[2] = 1.7548 + \frac{-0.2797+(-0.3149)}{2} = 1.4575

y[2] = 1.1697 + \frac{0.1545+0.1645}{2} = 1.3020

t[2] = t[0] + h = 0.5 +0.5 = 1

itera=2

t = 1, x = 1.4575, y = 1.3020, h = 0.5

continuar como tarea ...

Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ]

3. Algoritmo en Python

Planteamiento que se ingresan al algoritmo con el algoritmo rungekutta2_fg(fx,gx,x0,y0,z0,h,muestras), propuesto en

EDO con Runge-Kutta d2y/dx2

Al ejecutar el algoritmo se obtienen los siguientes resultados:

Runge-Kutta Segunda derivada
i  [ xi,  yi,  zi ]
   [ K1y,  K1z,  K2y,  K2z ]
0 [0. 2. 1.]
   [0. 0. 0. 0.]
1 [0.5      1.754875 1.16975 ]
  [-0.2      0.175   -0.29025  0.1645 ]
2 [1.       1.457533 1.302069]
  [-0.279749  0.154528 -0.314935  0.11011 ]
3 [1.5      1.167405 1.373599]
  [-0.29985   0.104254 -0.280406  0.038807]
4 [2.       0.922773 1.381103]
  [-0.26939   0.040241 -0.219874 -0.025233]
5 [2.5      0.734853 1.33689 ]
  [-0.215362 -0.018665 -0.160478 -0.069761]
6 [3.       0.598406 1.258434]
  [-0.160133 -0.062033 -0.11276  -0.09488 ]
...

Los resultados de la tabla se muestran parcialmente, pues se usaron mas de 100 iteraciones.

Los resultados se pueden observar de diferentes formas:

a) Cada variable x_i, y_i versus t_i, es decir cantidad de animales de cada especie durante el tiempo de observación

b) Independiente de la unidad de tiempo, x_i vs y_i, muestra la relación entre la cantidad de presas y predadores. Relación que es cíclica y da la forma a la gráfica.

Las instrucciones del algoritmo en Python usadas en el problema son:

# Modelo predador-presa de Lotka-Volterra
# Sistemas EDO con Runge Kutta de 2do Orden
import numpy as np

def rungekutta2_fg(f,g,x0,y0,z0,h,muestras,
                   vertabla=False, precision=6):
    ''' solucion a EDO d2y/dx2 con Runge-Kutta 2do Orden,
    f(x,y,z) = z #= y'
    g(x,y,z) = expresion d2y/dx2 con z=y'
    tambien es solucion a sistemas edo f() y g()
    x0,y0,z0 son valores iniciales, h es tamano de paso,
    muestras es la cantidad de puntos a calcular.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,3+4),dtype=float)
    # incluye el punto [x0,y0,z0,K1y,K1z,K2y,K2z]
    tabla[0] = [x0,y0,z0,0,0,0,0]
    
    xi = x0 # valores iniciales
    yi = y0
    zi = z0
    for i in range(1,tamano,1):
        K1y = h * f(xi,yi,zi)
        K1z = h * g(xi,yi,zi)
        
        K2y = h * f(xi+h, yi + K1y, zi + K1z)
        K2z = h * g(xi+h, yi + K1y, zi + K1z)

        yi = yi + (K1y+K2y)/2
        zi = zi + (K1z+K2z)/2
        xi = xi + h
        
        tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z]
        
    if vertabla==True:
        np.set_printoptions(precision)
        print('EDO f,g con Runge-Kutta 2 Orden')
        print('i ','[ xi,  yi,  zi',']')
        print('   [ K1y,  K1z,  K2y,  K2z ]')
        for i in range(0,tamano,1):  
            txt = ' '
            if i>=10:
                txt = '  '
            print(str(i),tabla[i,0:3])
            print(txt,tabla[i,3:])
    
    return(tabla)

# PROGRAMA ------------------

# INGRESO
# Parámetros de las ecuaciones
a = 0.5
b = 0.7
c = 0.35
d = 0.35

# Ecuaciones
f = lambda t,x,y : a*x -b*x*y
g = lambda t,x,y : -c*y + d*x*y

# Condiciones iniciales
t0 = 0
x0 = 2
y0 = 1

# parámetros del algoritmo
h = 0.5
muestras = 101

# PROCEDIMIENTO
tabla = rungekutta2_fg(f,g,t0,x0,y0,h,muestras,vertabla=True)
ti = tabla[:,0]
xi = tabla[:,1]
yi = tabla[:,2]

# SALIDA
print('Sistemas EDO: Modelo presa-predador')
##np.set_printoptions(precision=6)
##print(' [ ti, xi, yi]')
##print(tabla[:,0:4])

Los resultados numéricos se usan para generar las gráficas presentadas, añadiendo las instrucciones:

# GRAFICA tiempos vs población
import matplotlib.pyplot as plt

fig_t, (graf1,graf2) = plt.subplots(2)
fig_t.suptitle('Modelo predador-presa')
graf1.plot(ti,xi, color='blue',label='xi presa')

#graf1.set_xlabel('t tiempo')
graf1.set_ylabel('población x')
graf1.legend()
graf1.grid()

graf2.plot(ti,yi, color='orange',label='yi predador')
graf2.set_xlabel('t tiempo')
graf2.set_ylabel('población y')
graf2.legend()
graf2.grid()

# gráfica xi vs yi
fig_xy, graf3 = plt.subplots()
graf3.plot(xi,yi)

graf3.set_title('Modelo presa-predador [xi,yi]')
graf3.set_xlabel('x presa')
graf3.set_ylabel('y predador')
graf3.grid()
plt.show()

Sistemas EDO [ Ejercicio ] [ Analítico ] [ Algoritmo ] [ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ]

2017-09-052025-08-16

6.3 EDO d2y/dx2, Runge-Kutta con Python

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]
..

1. EDO $\frac{\delta^2 y}{\delta x^2}$ con Runge-Kutta

Para una ecuación diferencial de segunda derivada (segundo orden) con condiciones de inicio en x₀, y₀, y'₀

\frac{\delta ^2 y}{\delta x^2} = \frac{\delta y}{\delta x} + etc

Forma estandarizada de la ecuación:

y'' = y' + etc

Se puede sustituir la variable y' por z, lo que se convierte a dos expresiones que forman un sistema de ecuaciones:

\begin{cases} z= y' = f_x(x,y,z) \\ z' = (y')' = z + etc = g_x(x,y,z) \end{cases}

y se pueden reutilizar los métodos para primeras derivadas, por ejemplo Runge-Kutta de 2do y 4to orden para las variables x,y,z de forma simultanea.

Runge-Kutta 2do Orden tiene error de truncamiento O(h³)
Runge-Kutta 4do Orden tiene error de truncamiento O(h⁵)

Al aplicar Runge-Kutta para las variables dependientes, se tiene:

y'' = y' + etc

\begin{cases} f_x(x,y,z) = z \\ g_x(x,y,z) = z + etc \end{cases}

K_{1y} = h f(x_i, y_i, z_i)

K_{1z} = hg(x_i, y_i, z_i)

K_{2y} = h f(x_i +h, y_i + K_{1y} , z_i + K_{1z})

K_{2z} = h g(x_i +h, y_i + K_{1y}, z_i + K_{1z})

y_{i+1}=y_i+\frac{K_{1y}+K_{2y}}{2}

z_{i+1}=z_i+\frac{K_{1z}+K_{2z}}{2}

x_{i+1} = x_i +h

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]

2. Ejercicio

Referencia: Chapra Ejercicio 25.23 p265, 2Eva_IT2018_T1 Paracaidista wingsuit

Si suponemos que el arrastre es proporcional al cuadrado de la velocidad, se puede modelar la altura (y) de un objeto que cae, como un paracaidista, por medio de la ecuación diferencial ordinaria:

\frac{d^2y}{dt^2} = g - \frac{Cd}{m} \Big( \frac{dy}{dt} \Big) ^2

Que es una EDO de 2do orden o como 2da derivada.

Resuelva para la altura que recorre un objeto de 90 Kg con coeficiente de arrastre Cd =0.225 kg/m.

Si la velocidad inicial es 0 y la altura inicial es 1 Km, determine la velocidad y posición en cada tiempo, usando un tamaño de paso de 2s.

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]

3. Desarrollo analítico

La solución propone resolver de forma simultanea para t,y,v con Runge Kutta para segunda derivada donde:

f(t,y,v) = -v

g(t,y,v) = g - \frac{Cd}{m} v^2

Al sustituir los valores de las constantes en la ecuación como gravedad, masa e índice de arrastre se tiene:

f(t,y,v) = -v

g(t,y,v) = 9.8 - \frac{0.225}{90} v^2

con las condiciones iniciales del ejercicio t₀ = 0 , y₀ = 1000, v₀ = 0
la velocidad se inicia con cero, si el paracaidista se deja caer desde el borde el risco, como en el video adjunto al enunciado.

Para las iteraciones, recuerde que
t se corrige con t+h (en el algoritmo era la posición para x)
y se corrige con y+K1y
v se corrige con v+K1v (en el algoritmo era la posición para z)

itera = 0

K1y = h f(t,y,v) = 2(-(0)) = 0

K1v = h g(t,y,v) = 2(9.8 - \frac{0.225}{90} (0)^2) = 19.6

..
$K2y = h f(t+h, y+K1y, v + K1v) = 2(-(0 + 19.6)) = -39.2$

K2v = h g(t+h, y+K1y, v + K1v) = 2(9.8 - \frac{0.225}{90} (0+19.6)^2) =17.6792

..
$y_1 = y_0 + \frac{K1y+K2y}{2} = 1000 + \frac{0-39.2}{2}= 980.4$

v_1 = v_0 + \frac{K1v+K2v}{2} = 0 + \frac{19.6-17.67}{2} = 18.63

t_1 =t_0 + h = 0+2 = 2

ti	yi	vi	K1y	K1v	K2y	K2v
0	1000	0	0	0	0	0
2	980.4	18.63	0	19.6	-39.2	17.6792

itera = 1

K1y = 2(-(18.63)) = -37.2792

K1v = 2(9.8 - \frac{0.225}{90} (18.63)^2) = 17.8628

..
$K2y =2(-(18.6396+17.8628)) =-73.00$

K2v = 2(9.8 - \frac{0.225}{90} (18.6396+17.8628)^2) =12.9378

..
$y_2 =980.4 + \frac{ -37.2792+(-73.00)}{2}= 925.25$

v_2 = 18.63 + \frac{17.8628+12.9378}{2} = 34.0399

t_2 =t_1 + h = 2+2 = 4

ti	yi	vi	K1y	K1v	K2y	K2v
0	1000	0	0	0	0	0
2	980.4	18.63	0	19.6	-39.2	17.6792
4	925.25	34.0399	-37.2792	17.8628	-73.00	12.9378

itera = 2

K1y = h f(t,y,v) = 2(-(34.0399)) = -68.0798

K1v = h g(t,y,v) = 2(9.8 - \frac{0.225}{90} (34.0399)^2) = 13.8064

..
$K2y = h f(t+h, y+K1y, v + K1v) = 2(-(34.0399+13.8064)) =-95.6927$

K2v = h g(t+h, y+K1y, v + K1v) = 2(9.8 - \frac{0.225}{90} (34.0399+13.8064)^2) =8.1536

..
$y_2 = 925.25 + \frac{ -68.0798+(-95.6927)}{2}= 843.3716$

v_2 = 34.0399 + \frac{13.8064+8.1536}{2} = 45.0199

t_2 =t_1 + h = 4+2 = 6

ti	yi	vi	K1y	K1v	K2y	K2v
0	1000	0	0	0	0	0
2	980.4	18.63	0	19.6	-39.2	17.6792
4	925.25	34.0399	-37.2792	17.8628	-73.00	12.9378
6	843.3716	45.0199	-68.0798	13.8064	-95.6927	8.1536

Usando el algoritmo se obtiene el siguiente resultado:

EDO f,g con Runge-Kutta 2 Orden
i  [ xi,  yi,  zi ]
   [ K1y,  K1z,  K2y,  K2z ]
0 [   0. 1000.    0.]
  [0. 0. 0. 0.]
1 [  2.     980.4     18.6396]
  [  0.      19.6    -39.2     17.6792]
2 [  4.     925.258   34.0399]
  [-37.2792  17.8628 -73.0049  12.9379]
3 [  6.     843.3717  45.02  ]
  [-68.0799  13.8064 -95.6927   8.1536]
4 [  8.     743.8657  52.1312]
  [ -90.0399    9.466  -108.972     4.7564]
5 [ 10.     633.5917  56.4855]
  [-104.2623    6.0117 -116.2857    2.697 ]
6 [ 12.     516.9737  59.0692]

con la siguiente gráfica

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]

4. Algoritmo en Python para $\frac{\delta^2 y}{\delta x^2}$ Runge-Kutta 2do Orden

Se presenta las instrucciones en Python con una función.

# EDO d2y/dx2. Método de RungeKutta 2do Orden 
# estima la solucion para muestras espaciadas h en eje x
# valores iniciales x0,y0,z0 entrega tabla[xi,yi,zi,K1y,K1z,K2y,K2z]
import numpy as np

def rungekutta2_fg(f,g,x0,y0,z0,h,muestras,
                   vertabla=False, precision=6):
    ''' solucion a EDO d2y/dx2 con Runge-Kutta 2do Orden,
    f(x,y,z) = z #= y'
    g(x,y,z) = expresion d2y/dx2 con z=y'
    tambien es solucion a sistemas edo f() y g()
    x0,y0,z0 son valores iniciales, h es tamano de paso,
    muestras es la cantidad de puntos a calcular.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,3+4),dtype=float)
    # incluye el punto [x0,y0,z0,K1y,K1z,K2y,K2z]
    tabla[0] = [x0,y0,z0,0,0,0,0]
    
    xi = x0 # valores iniciales
    yi = y0
    zi = z0
    for i in range(1,tamano,1):
        K1y = h * f(xi,yi,zi)
        K1z = h * g(xi,yi,zi)
        
        K2y = h * f(xi+h, yi + K1y, zi + K1z)
        K2z = h * g(xi+h, yi + K1y, zi + K1z)

        yi = yi + (K1y+K2y)/2
        zi = zi + (K1z+K2z)/2
        xi = xi + h
        
        tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z]
        
    if vertabla==True:
        np.set_printoptions(precision)
        print('EDO f,g con Runge-Kutta 2 Orden')
        print('i ','[ xi,  yi,  zi',']')
        print('   [ K1y,  K1z,  K2y,  K2z ]')
        for i in range(0,tamano,1):  
            txt = ' '
            if i>=10:
                txt = '  '
            print(str(i),tabla[i,0:3])
            print(txt,tabla[i,3:])
    
    return(tabla)

# PROGRAMA PRUEBA -------------------
# 2Eva_IT2018_T1 Paracaidista wingsuit

# INGRESO
f = lambda t,y,v: -v # el signo, revisar diagrama cuerpo libre
g = lambda t,y,v: 9.8 - (0.225/90)*(v**2)
t0 = 0
y0 = 1000
v0 = 0
h  = 2
muestras = 15+1

# PROCEDIMIENTO
tabla = rungekutta2_fg(f,g,t0,y0,v0,h,muestras,
                       vertabla=True, precision=4)
ti = tabla[:,0]
yi = tabla[:,1]
vi = tabla[:,2]

# SALIDA
# print('tabla de resultados')
# print(tabla)

# GRAFICA
import matplotlib.pyplot as plt
plt.subplot(211)
plt.plot(ti,vi,label='velocidad v(t)', color='green')
plt.plot(ti,vi,'o')
plt.ylabel('velocidad (m/s)')
plt.title('paracaidista Wingsuit con Runge-Kutta')
plt.legend()
plt.grid()

plt.subplot(212)
plt.plot(ti,yi,label='Altura y(t)',)
plt.plot(ti,yi,'o',)
plt.axhline(0, color='red')
plt.xlabel('tiempo (s)')
plt.ylabel('Altura (m)')
plt.legend()
plt.grid()

plt.show()

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]
..

5. Algoritmo en Python para $\frac{\delta^2 y}{\delta x^2}$ Runge-Kutta 4to Orden

Se adjunta la función para 4to orden que se puede probar con el mismo ejercicio anterior.

# EDO d2y/dx2. Método de RungeKutta 4to Orden 
# estima la solucion para muestras espaciadas h en eje x
# valores iniciales x0,y0,z0 entrega
# tabla[xi,yi,zi,K1y,K1z,K2y,K2z,K3y,K3z,K4y,K4z]
import numpy as np

def rungekutta4_fg(fx,gx,x0,y0,z0,h,muestras,
                   vertabla=False, precision=6):
    ''' solucion a EDO d2y/dx2 con Runge-Kutta 4to Orden,
    f(x,y,z) = z #= y'
    g(x,y,z) = expresion d2y/dx2 con z=y'
    tambien es solucion a sistemas edo f() y g()
    x0,y0,z0 son valores iniciales, h es tamano de paso,
    muestras es la cantidad de puntos a calcular.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,3+8),dtype=float)
    # incluye el punto [x0,y0]
    tabla[0] = [x0,y0,z0,0,0,0,0,0,0,0,0]

    xi = x0 # valores iniciales
    yi = y0
    zi = z0
    for i in range(1,tamano,1):
        K1y = h * fx(xi,yi,zi)
        K1z = h * gx(xi,yi,zi)
        
        K2y = h * fx(xi+h/2, yi + K1y/2, zi + K1z/2)
        K2z = h * gx(xi+h/2, yi + K1y/2, zi + K1z/2)
        
        K3y = h * fx(xi+h/2, yi + K2y/2, zi + K2z/2)
        K3z = h * gx(xi+h/2, yi + K2y/2, zi + K2z/2)

        K4y = h * fx(xi+h, yi + K3y, zi + K3z)
        K4z = h * gx(xi+h, yi + K3y, zi + K3z)

        yi = yi + (K1y+2*K2y+2*K3y+K4y)/6
        zi = zi + (K1z+2*K2z+2*K3z+K4z)/6
        xi = xi + h
        
        tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z,K3y,K3z,K4y,K4z]
    
    if vertabla==True:
        np.set_printoptions(precision)
        print('EDO f,g con Runge-Kutta 4 Orden')
        print('i ','[ xi,  yi,  zi',']')
        print('   [ K1y,  K1z,  K2y,  K2z ]')
        print('   [ K3y,  K3z,  K4y,  K4z ]')
        for i in range(0,tamano,1):  
            txt = ' '
            if i>=10:
                txt = '  '
            print(str(i),tabla[i,0:3])
            print(txt,tabla[i,3:7])
            print(txt,tabla[i,7:])

    return(tabla)

[ Runge Kutta $\frac{\delta^2 y}{\delta x^2}$ ] [ Ejercicio ] [ analítico ]
Algoritmo: [ RK 2do Orden ] [ RK 4to Orden]

2017-09-042025-08-16

6.2.1 EDO dy/dx, Runge-Kutta 4to Orden con Python

[ Runge Kutta 4to Orden ] [ Función ] [ Ejercicio en video ]

EDO $\frac{\delta y}{\delta x}$ Runge-Kutta 4to Orden

Referencia: Chapra 25.3.3 p746, Rodríguez 9.1.8 p358

Para una ecuación diferencial de primera derivada (primer orden) con una condición de inicio:

\frac{\delta y}{\delta x} + etc =0

y'(x) = f(x_i,y_i)

y(x_0) = y_0

La fórmula de Runge-Kutta de 4to orden realiza una corrección con 4 valores de K:

y_{i+1} = y_i + \frac{K_1 + 2K_2 + 2K_3 + K_4}{6}

debe ser equivalente a la serie de Taylor de 5 términos:

y_{i+1} = y_i + h f(x_i,y_i) +

+ \frac{h^2}{2!} f'(x_i,y_i) + \frac{h^3}{3!} f''(x_i,y_i) +

+\frac{h^4}{4!} f'''(x_i,y_i) + O(h^5)

x_{i+1} = x_i + h

Runge-Kutta 4do Orden tiene error de truncamiento O(h⁵)

Ejercicio

Para el desarrollo analítico se tienen las siguientes expresiones para el ejercicio usado en Runge-Kutta de orden 2, que ahora será con orden 4:

f(x,y) = y' = y -x^2 +x +1

Se usa las expresiones de Runge-Kutta en orden, K1 corresponde a una corrección de EDO con Taylor de dos términos (método de Euler). K2 considera el cálculo a medio tamaño de paso más adelante.

iteración:

K_1 = h f(x_i,y_i) = 0.1 (y_i -x_i^2 +x_i +1)

K_2 = h f\Big(x_i+\frac{h}{2}, y_i + \frac{K_1}{2} \Big)

K_2 = 0.1 \Big(\big(y_i+\frac{K_1}{2}\big) -\big(x_i+\frac{h}{2}\big)^2 +\big(x_i+\frac{h}{2}\big) +1 \Big)

K_3 = h f\Big(x_i+\frac{h}{2}, y_i + \frac{K_2}{2} \Big)

K_3 = 0.1 \Big(\big(y_i+\frac{K_2}{2}\big) -\big(x_i+\frac{h}{2}\big)^2 +\big(x_i+\frac{h}{2}\big) +1 \Big)

K_4 = h f(x_i+h, y_i + K_3 )

K_4 = 0.1 \Big((y_i+K_3) -(x_i+h)^2 +(x_i+h) +1 \Big)

y_{i+1} = y_i + \frac{K_1+2K_2+2K_3+K_4}{6}

x_{i+1} = x_i + h

Las iteraciones se dejan como tarea

[ Runge Kutta 4to Orden ] [ Función ] [ Ejercicio en video ]

Algoritmo en Python como Función

def rungekutta4(d1y,x0,y0,h,muestras, vertabla=False, precision=6):
    ''' solucion a EDO con Runge-Kutta 4do Orden primera derivada,
        x0,y0 son valores iniciales, tamaño de paso h.
        muestras es la cantidad de puntos a calcular.
    '''
    # Runge Kutta de 4do orden
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,2+4),dtype=float)
    
    # incluye el punto [x0,y0,K1,K2,K3,K4]
    tabla[0] = [x0,y0,0,0,0,0]
    xi = x0
    yi = y0
    for i in range(1,tamano,1):
        K1 = h * d1y(xi,yi)
        K2 = h * d1y(xi+h/2, yi + K1/2)
        K3 = h * d1y(xi+h/2, yi + K2/2)
        K4 = h * d1y(xi+h, yi + K3)

        yi = yi + (1/6)*(K1+2*K2+2*K3 +K4)
        xi = xi + h
        
        tabla[i] = [xi,yi,K1,K2,K3,K4]
        
    if vertabla==True:
        np.set_printoptions(precision)
        titulo = ' [xi,     yi,     K1,    K2,     K3,     K4 ]'
        print(' EDO con Runge-Kutta 4do Orden primera derivada')
        print(titulo)
        print(tabla)
    return(tabla)

Note que el método de Runge-Kutta de 4to orden es similar a la regla de Simpson 1/3. La ecuación representa un promedio ponderado para establecer la mejor pendiente.

[ Runge Kutta 4to Orden ] [ Función ] [ Ejercicio en video ]

Ejercicio

2Eva_IT2018_T1 Paracaidista wingsuit

Solución Propuesta: s2Eva_IT2018_T1 Paracaidista wingsuit

La segunda parte corresponde a Runge-Kutta de 4to Orden

[ Runge Kutta 4to Orden ] [ Función ] [ Ejercicio en video ]

2017-09-032025-09-01

6.2 EDO dy/dx, Runge-Kutta con Python

[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

1. EDO $\frac{\delta y}{\delta x}$ con Runge-Kutta de 2do Orden

Referencia: Burden 5.4 p209, Chapra 25.3 p740, Rodríguez 9.1.7 p354, Boyce DiPrima 4Ed 8.4 p450

Para una ecuación diferencial ordinaria de primera derivada, el método Runge-Kutta de 2do Orden usa una corrección sobre la derivada a partir de los puntos xi y xi+h, es decir un tamaño de paso h hacia adelante, calculados como términos K₁ y K₂.

Considere una ecuación diferencial de primera derivada con una condición de inicio se reordena y se escribe como f(x,y) siguiendo los pasos:

\frac{\delta y}{\delta x} + etc =0

y'(x) = f(x_i,y_i)

y(x_0) = y_0

Los términos K₁ y K₂ se calculan para predecir el próximo valor en y[i+1], observe que el término K₁ es el mismo que el método de Edo con Taylor de dos términos.

K_1 = h f(x_i,y_i)

K_2 = h f(x_i+h, y_i + K_1)

y_{i+1} = y_i + \frac{K_1+K_2}{2}

x_{i+1} = x_i + h

Runge-Kutta 2do Orden tiene error de truncamiento O(h³)

Las iteraciones se repiten para encontrar el siguiente punto en x[i+1] como se muestra en el gráfico animado.

Los métodos de Runge-Kutta mejoran la aproximación a la respuesta de la ecuación diferencial ordinaria sin requerir determinar las expresiones de las derivadas de orden superior, como fue necesario en EDO con Taylor.

Para observar al idea básica, considere observar un combate aéreo simulado en la década de 1940, donde las armas se encuentras fijas en las alas del avión. Observe dos minutos del video sugerido a partir de donde se encuentra marcado el enlace.

Video Revisar:

Luego de observar el video de introducción conteste las siguientes preguntas:
¿ Que trayectoria siguen los proyectiles al salir del cañón?
¿ Que trayectoria siguen los aviones, el perseguido y el que caza?
¿ Cuál es la relación entre las trayectorias de los dos aviones?

[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

2. Ejercicio

Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731

Se pide encontrar puntos de la solución en la ecuación diferencial usando los tres primeros términos de la serie de Taylor con h=0.1 y punto inicial x₀=0, y₀=1

\frac{dy}{dx}-y -x +x^2 -1 = 0

y'-y -x +x^2 -1 = 0

[ Runge Kutta dy/dx] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

3. Desarrollo Analítico

Se reordena la expresión haciendo que la derivada se encuentre en el lado izquierdo:

f(x,y) = y' = y -x^2 +x +1

Se usa las expresiones de Runge-Kutta en orden, K1 corresponde a una corrección de EDO con Taylor de dos términos (método de Euler). K2 considera el cálculo a un tamaño de paso más adelante. iteración:

K_1 = h f(x_i,y_i) = 0.1 (y_i -x_i^2 +x_i +1)

K_2 = h f(x_i+h, y_i + K_1)

K_2 = 0.1 \Big((y_i+K_1) -(x_i+h)^2 +(x_i+h) +1 \Big)

y_{i+1} = y_i + \frac{K_1+K_2}{2}

x_{i+1} = x_i + h

Runge-Kutta 2do Orden tiene error de truncamiento O(h³)

para el ejercicio, el tamaño de paso h=0.1, se realizan tres iteraciones en las actividades del curso con lápiz y papel,

itera = 0 , x₀ = 0, y₀ = 1

K_1 = 0.1 f(0,1) = 0.1 \Big( 1 -0^2 +0 +1 \Big) = 0.2

K_2 = 0.1 f(0+0.1, 1+ 0.2)

K_2 = 0.1 \Big( (1+ 0.2) - (0+0.1) ^2 +(0+0.1) +1\Big) = 0.229

y_1 = 1 + \frac{0.2+0.229}{2} = 1.2145

x_1 = 0 + 0.1 = 0.1

itera = 1 , x₁ = 0.1, y₁ = 1.2145

K_1 = 0.1 f(0.1,1.2145)

= 0.1( 1.2145 -0.1^2 +0.1 +1)

K_1 = 0.2304

K_2 = 0.1 f(0.1+0.1, 1.2145 + 0.2304)

=0.1 \Big((1.2145 + 0.2304) -(0.1+0.1)^2 +(0.1+0.1) +1\Big)

K_2 = 0.2604

y_2 = 1.2145 + \frac{0.2304+0.2604}{2} = 1.4599

x_2 = 0.1 +0.1 = 0.2

itera = 2 , x₂ = 0.2, y₂ = 1.4599

K_1 = 0.1 f(0.2,1.4599)

= 0.1( 1.4599 -0.2^2 +0.2 +1)

K_1 = 0.2619

K_2 = 0.1 f(0.2+0.1, 1.4599 + 0.2619)

=0.1 \Big((1.4599 + 0.2619) -(0.2+0.1)^2 +(0.2+0.1) +1\Big)

K_2 = 0.2931

y_2 = 1.4599 + \frac{0.2619+0.2931}{2} = 1.7375

x_2 = 0.2 +0.1 = 0.3

luego de las 3 iteraciones en papel, se completan los demás puntos con el algoritmo obteniendo la gráfica resultante para y(x) correspondiente.

EDO dy/dx con Runge-Kutta 2 Orden
i, [xi,     yi,     K1,    K2]
0 [0. 1. 0. 0.]
1 [0.1    1.2145 0.2    0.229 ]
2 [0.2      1.459973 0.23045  0.260495]
3 [0.3      1.73757  0.261997 0.293197]
4 [0.4      2.048564 0.294757 0.327233]
5 [0.5      2.394364 0.328856 0.362742]
>>>

Compare los resultados con Taylor de 2 y 3 términos.

Runge-Kutta 2do Orden tiene error de truncamiento O(h³)

[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

4. Algoritmo en Python

Para el ejercicio anterior, se adjunta el programa de prueba que usa la función rungekutta2(d1y,x0,y0,h,muestras) .

Las iteraciones y sus valores se pueden observar usando vertabla=true

# EDO dy/dx. M todo de RungeKutta 2do Orden 
# estima la solucion para muestras espaciadas h en eje x
# valores iniciales x0,y0, entrega tabla[xi,yi,K1,K2]
import numpy as np

def rungekutta2(d1y,x0,y0,h,muestras,
                vertabla=False,precision=6):
    '''solucion a EDO dy/dx, con Runge Kutta de 2do orden
    d1y es la expresi n dy/dx, tambien planteada como f(x,y),
    valores iniciales: x0,y0, tama o de paso h.
    muestras es la cantidad de puntos a calcular. 
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,2+2),dtype=float)
    tabla[0] = [x0,y0,0,0] # incluye el punto [x0,y0]
    
    xi = x0 # valores iniciales
    yi = y0
    for i in range(1,tamano,1):
        K1 = h * d1y(xi,yi)
        K2 = h * d1y(xi+h, yi + K1)

        yi = yi + (K1+K2)/2
        xi = xi + h
        
        tabla[i] = [xi,yi,K1,K2]
       
    if vertabla==True:
        np.set_printoptions(precision)
        print( 'EDO dy/dx con Runge-Kutta 2 Orden')
        print('i, [xi,     yi,     K1,    K2]')
        for i in range(0,tamano,1):
            print(i,tabla[i])

    return(tabla)

# PROGRAMA PRUEBA -------------------

# INGRESO
# d1y = y' = f
d1y = lambda x,y: y -x**2 + x + 1
x0 = 0
y0 = 1
h  = 0.1
muestras = 5

# PROCEDIMIENTO
tabla = rungekutta2(d1y,x0,y0,h,muestras,
                    vertabla=True)
xi = tabla[:,0]
yiRK2 = tabla[:,1]

# SALIDA
#print(' [xi, yi, K1, K2]')
#print(tabla)

# GRAFICA
import matplotlib.pyplot as plt
plt.plot(xi,yiRK2)
plt.plot(xi[0],yiRK2[0],
         'o',color='r', label ='[x0,y0]')
plt.plot(xi[1:],yiRK2[1:],
         'o',color='m',
         label ='[xi,yi] Runge-Kutta')
plt.title('EDO dy/dx: Runge-Kutta 2do Orden')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

5. Cálculo de Error con la solución conocida

La ecuación diferencial ordinaria del ejercicio tiene una solución conocida, lo que permite encontrar el error real en cada punto respecto a la aproximación estimada.

y = e^x + x + x^2

Note que el error crece al distanciarse del punto inicial.

Error máximo estimado:  0.004357584597315167
entre puntos: 
[0.         0.00067092 0.00143026 
 0.0022892  0.00326028 0.00435758]
>>>

Para las siguientes instrucciones, comente la última línea #plt.show() antes de continuar con:

# ERROR vs solución conocida -----------------
y_sol = lambda x: ((np.e)**x) + x + x**2

yi_psol  = y_sol(xi)
errores  = yi_psol - yiRK2
errormax = np.max(np.abs(errores))

# SALIDA
print('Error máximo estimado: ',errormax)
print('entre puntos: ')
print(errores)

# GRAFICA [a,b+2*h]
a = x0
b = h*muestras+2*h
muestreo = 10*muestras+2
xis = np.linspace(a,b,muestreo)
yis = y_sol(xis)

plt.plot(xis,yis, label='y solución conocida',
         linestyle='dashed')
plt.legend()
plt.show()

[ Runge Kutta dy/dx ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

6. Ejercicio de Evaluación

2Eva_IT2018_T1 EDO Paracaidista wingsuit

Solución Propuesta: s2Eva_IT2018_T1 EDO Paracaidista wingsuit , Runge-Rutta para primera derivada.

2017-09-022025-08-16

6.1 EDO con Taylor de 3 términos con Python

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

1. Ecuaciones diferenciales ordinarias aproximadas con Taylor

Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731

En los métodos con Taylor para Ecuaciones Diferenciales Ordinarias (EDO) se aproxima el resultado a n términos de la serie, para lo cual se ajusta la expresión del problema a cada derivada correspondiente.

La solución empieza usando la Serie de Taylor para tres términos ajustada a la variable del ejercicio:

y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i

x_{i+1} = x_{i} + h

E = \frac{h^3}{3!} y'''(z) = O(h^3)

A partir de la expresión de y'(x) y el punto inicial conocido en x[i],se busca obtener el próximo valor en x[i+1] al avanzar un tamaño de paso h. Se repite el proceso en el siguiente punto encontrado y se continua hasta alcanzar el intervalo objetivo.

En éstos métodos la solución siempre es una tabla de puntos xi,yi que se pueden usar para interpolar y obtener una función polinómica.

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

2. Ejercicio

Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731

Se requiere encontrar puntos de la solución en la ecuación diferencial usando los tres primeros términos de la serie de Taylor con h=0.1 y punto inicial x₀=0, y₀=1

\frac{dy}{dx}-y -x +x^2 -1 = 0

que con nomenclatura simplificada:

y'-y -x +x^2 -1 = 0

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

3. Desarrollo Analítico

Al despejar el valor de y' de expresión del ejercicio,

y' = y -x^2 +x +1

se puede obtener y" al derivar una vez,

y'' = y' -2x + 1

para luego combinar las expresiones en

y'' = (y -x^2 +x +1) -2x + 1

simplificando:

y'' = y -x^2 -x +2

Ecuaciones que permiten estimar nuevos valores y_i+1 para nuevos puntos muestra distanciados en i*h desde el punto inicial siguiendo las siguientes expresiones de iteración:

y'_i = y_i -x_i^2 + x_i +1

y''_i = y_i -x_i^2 - x_i +2

y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i

x_{i+1} = x_{i} + h

Se empieza evaluando el nuevo punto a una distancia x₁= x₀+h del punto de origen con lo que se obtiene y₁ , repitiendo el proceso para el siguiente punto en forma sucesiva.

itera = 0 , x0 = 0, y0 = 1

y'_0 = 1 -0^2 +0 +1 = 2

y''_0 = 1 -0^2 -0 +2 = 3

y_1 = y_{0} + h y'_0 + \frac{h^2}{2!} y''_0

y_1 = 1 + 0.1 (2) + \frac{0.1^2}{2!} 3 = 1.215

x_1 = 0 + 0.1

itera = 1 , x = 0.1, y = 1.215

y'_1 = 1.215 - 0.1^2 + 0.1 +1 = 2.305

y''_1 = 1.215 - 0.1^2 - 0.1 +2 = 3.105

y_2 = 1.215 + 0.1 (2.305) + \frac{0.1^2}{2!} 3.105 = 1.461

x_2 = 0.1 + 0.1 = 0.2

itera = 2 , x = 0.2, y = 1.461

y'_2 = 1.461 - 0.2^2 + 0.2 +1 = 2.621

y''_2 = 1.461 - 0.2^2 - 0.2 +2 = 3.221

y_3 = 1.461 + 0.1 (2.621) + \frac{0.1^2}{2!} 3.221 = 1.7392

x_3 = 0.2 + 0.1 = 0.3

completando los puntos con el algoritmo y realizando la gráfica se obtiene

 EDO con Taylor 3 términos
[xi, yi, d1yi, d2yi]
[[0.         1.         0.         0.        ]
 [0.1        1.215      2.         3.        ]
 [0.2        1.461025   2.305      3.105     ]
 [0.3        1.73923262 2.621025   3.221025  ]
 [0.4        2.05090205 2.94923262 3.34923262]
 [0.5        2.39744677 3.29090205 3.49090205]]
>>>

Observación, note que los resultados de las derivadas, se encuentran desplazados una fila para cada iteración. Asunto a ser considerado en la gráfica de las derivadas en caso de incluirlas.

Nota: Compare luego los pasos del algoritmo con el método de Runge-Kutta de 2do orden.

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..

4. Algoritmo en Python

Para simplificar los cálculos se crea una función edo_taylor3t() para encontrar los valores para una cantidad de muestras distanciadas entre si h veces del punto inicial [x₀,y₀]

# EDO. Método de Taylor con3 términos 
# estima solucion para muestras separadas h en eje x
# valores iniciales x0,y0
import numpy as np

def edo_taylor3t(d1y,d2y,x0,y0,h,muestras):
    ''' solucion a EDO usando tres términos de Taylor, x0,y0 son valores iniciales
        muestras es la cantidad de puntos a calcular con tamaño de paso h.
    '''
    tamano = muestras + 1
    tabla = np.zeros(shape=(tamano,4),dtype=float)
    # incluye el punto [x0,y0]
    tabla[0] = [x0,y0,0,0]
    x = x0
    y = y0
    for i in range(1,tamano,1):
        d1yi = d1y(x,y)
        d2yi = d2y(x,y)
        y = y + h*d1yi + ((h**2)/2)*d2yi
        x = x + h
        tabla[i] = [x,y,d1yi,d2yi]
    return(tabla)

# PROGRAMA PRUEBA -----------------
# Ref Rodriguez 9.1.1 p335 ejemplo.
# prueba y'-y-x+(x**2)-1 =0, y(0)=1

# INGRESO.
# d1y = y', d2y = y''
d1y = lambda x,y: y - x**2 + x + 1
d2y = lambda x,y: y - x**2 - x + 2
x0 = 0
y0 = 1
h = 0.1
muestras = 5

# PROCEDIMIENTO
tabla = edo_taylor3t(d1y,d2y,x0,y0,h,muestras)
xi = tabla[:,0]
yi = tabla[:,1]

# SALIDA
print(' EDO con Taylor 3 términos')
print('[xi, yi, d1yi, d2yi]')
print(tabla)

# Gráfica
import matplotlib.pyplot as plt
plt.plot(xi,yi)
plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]')
plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada')
plt.title('EDO: Solución con Taylor 3 términos')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show() # plt.show() #comentar para la siguiente gráfica

Tarea: Realizar el ejercicio con más puntos muestra, donde se visualice que el error aumenta al aumentar la distancia del punto inicial [x₀,y₀]

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

5. Cálculo de Error con la solución conocida

La ecuación diferencial ordinaria del ejercicio tiene una solución conocida, lo que permite encontrar el error real en cada punto respecto a la aproximación estimada.

y = e^x + x + x^2

Note que el error crece al distanciarse del punto inicial

Para las siguientes instrucciones, comente la última línea #plt.show() antes de continuar con:

# ERROR vs solución conocida
y_sol = lambda x: ((np.e)**x) + x + x**2

yi_psol = y_sol(xi)
errores = yi_psol - yi
errormax = np.max(np.abs(errores))

# SALIDA
print('Error máximo estimado: ',errormax)
print('entre puntos: ')
print(errores)

# GRAFICA [a,b+2*h]
a = x0
b = h*muestras+2*h
muestreo = 10*muestras+2
xis = np.linspace(a,b,muestreo)
yis = y_sol(xis)

plt.plot(xis,yis,linestyle='dashed', label='y solución conocida')
plt.legend()
plt.show()

Se puede observar los siguientes resultados:

Error máximo estimado:  0.0012745047595
entre puntos: 
[ 0.  0.000170  0.000377  0.000626  0.000922  0.00127 ]

[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]

Differential equations, a tourist's guide | DE1. 3Blue1Brown. 31-mayo-2019
Los Fundamentos de Ecuaciones Diferenciales que Nadie te Explica. 3Blue1Brown Español. 19-Junio-2024

Por eso estás aprendiendo ecuaciones diferenciales. Zach Star. 9-junio-2020.

1. Ejercicio

2. Desarrollo Analítico

Algoritmos en Python

1. Ejercicio

2. Método Explícito

3. Algoritmo en Python

1. EDP Parabólicas

But what is a partial differential equation? | DE2

EDO con Taylor de 3 términos

Instrucciones en Python

Runge Kutta de 2do Orden para primera derivada

Sistemas EDO. modelo depredador-presa con Runge-Kutta 2do Orden .

1. Ejercicio

2. Desarrollo analítico

3. Algoritmo en Python

1. EDO \frac{\delta^2 y}{\delta x^2} con Runge-Kutta

2. Ejercicio

3. Desarrollo analítico

4. Algoritmo en Python para \frac{\delta^2 y}{\delta x^2} Runge-Kutta 2do Orden

5. Algoritmo en Python para \frac{\delta^2 y}{\delta x^2} Runge-Kutta 4to Orden

EDO \frac{\delta y}{\delta x} Runge-Kutta 4to Orden

Ejercicio

Algoritmo en Python como Función

Ejercicio

1. EDO \frac{\delta y}{\delta x} con Runge-Kutta de 2do Orden

2. Ejercicio

3. Desarrollo Analítico

4. Algoritmo en Python

5. Cálculo de Error con la solución conocida

6. Ejercicio de Evaluación

1. Ecuaciones diferenciales ordinarias aproximadas con Taylor

2. Ejercicio

3. Desarrollo Analítico

4. Algoritmo en Python

5. Cálculo de Error con la solución conocida

Sistemas EDO. modelo depredador-presa con Runge-Kutta 2do Orden
.

1. EDO $\frac{\delta^2 y}{\delta x^2}$ con Runge-Kutta

4. Algoritmo en Python para $\frac{\delta^2 y}{\delta x^2}$ Runge-Kutta 2do Orden

5. Algoritmo en Python para $\frac{\delta^2 y}{\delta x^2}$ Runge-Kutta 4to Orden

EDO $\frac{\delta y}{\delta x}$ Runge-Kutta 4to Orden

1. EDO $\frac{\delta y}{\delta x}$ con Runge-Kutta de 2do Orden