EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]
..
1. Ejercicio
Referencia: Chapra 30.2 p888 pdf912, Burden 9Ed 12.2 p725, Rodríguez 10.2 p406
Siguiendo el tema anterior en EDP Parabólicas, para resolver la parte numérica considere
Valores de frontera: Ta = 60, Tb = 40, T0 = 25
Longitud en x a = 0, b = 1, Constante K= 4
Tamaño de paso dx = 0.1, dt = dx/10
Para la ecuación diferencial parcial parabólica:
\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}2. Método Explícito
Se usan las diferencias divididas, donde se requieren dos valores para la derivada de orden uno y tres valores para la derivada de orden dos:
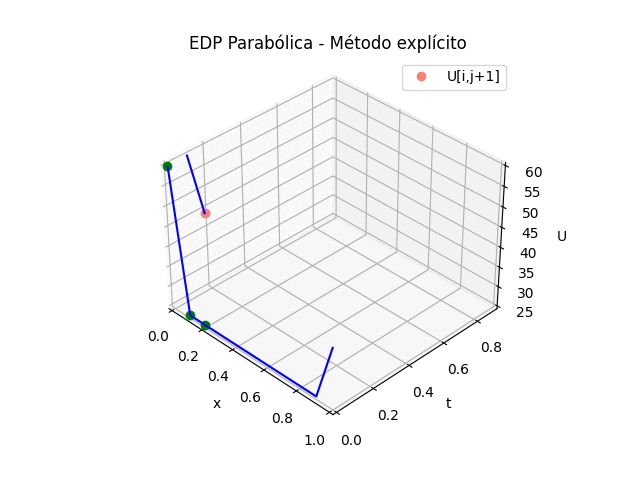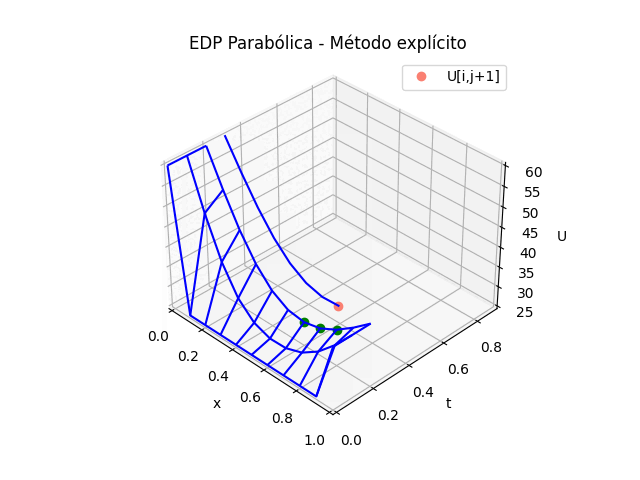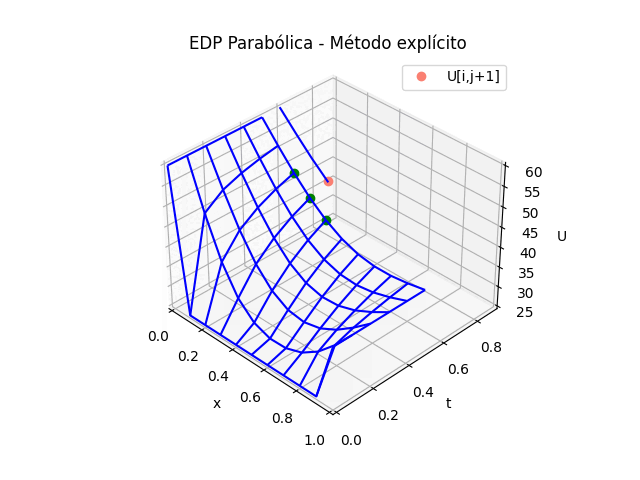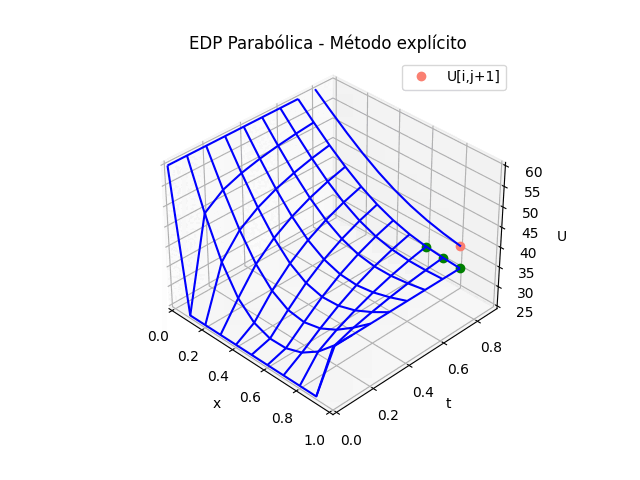
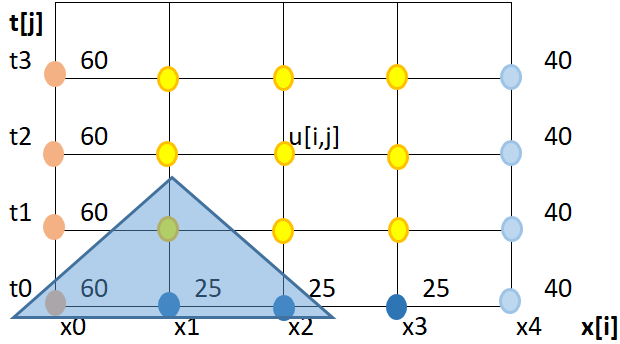
\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{\partial u}{\partial t} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla. La línea de referencia es el tiempo t0
Luego se sustituyen en la ecuación del problema, obteniendo:
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j+1}-u_{i,j}}{\Delta t}De la gráfica se destaca que en la fórmula solo hay un valor desconocido, destacado por el punto en amarillo dentro del triángulo. En la ecuación se representa por U[i,j+1].
Despejando la ecuación, se agrupan términos constantes:
λ = \frac{\Delta t}{K (\Delta x)^2}quedando la ecuación, con los términos ordenados de izquierda a derecha como en la gráfica:
u_{i,j+1} = \lambda u_{i-1,j} +(1-2\lambda)u_{i,j}+\lambda u_{i+1,j}Al resolver se encuentra que que cada valor en un punto amarillo se calcula como una suma ponderada de valores conocidos, por lo que el desarrollo se conoce como el método explícito.
La ponderación está determinada por los términos P, Q, y R.
\lambda = \frac{\Delta t}{K(\Delta x)^2} P = \lambda Q = 1-2\lambda R = \lambda u_{i ,j+1} = Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j}Fórmulas que se desarrollan usando un algoritmo y considerando que al disminuir los valores de Δx y Δt la cantidad de operaciones aumenta.
Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada.
Revisar los criterios en: Chapra 30.2.1 p891 pdf915, Burden 9Ed 12.2 p727, Rodríguez 10.2.2 pdf409 .
\lambda \leq \frac{1}{2}Cuando λ ≤ 1/2 se tiene como resultado una solución donde los errores no crecen, sino que oscilan.
Haciendo λ ≤ 1/4 asegura que la solución no oscilará.
También se sabe que con λ= 1/6 se tiende a minimizar los errores por truncamiento (véase Carnahan y cols., 1969).
Para resolver la parte numérica considere que:
Valores de frontera: Ta = 60, Tb = 40, Tc = 25 Longitud en x: a = 0, b = 1 Constante K = 4 Tamaño de paso dx = 0.1, dt = dx/10
EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]
..
3. Algoritmo en Python
Se muestra una tabla resumida de resultados a forma de ejemplo.
Método explícito EDP Parabólica lambda: 0.25 x: [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ] t: [0. 0.01 0.02 0.03 0.04] ... 1.0 Tabla de resultados en malla EDP Parabólica j, U[:,: 5 ], primeras iteraciones de 100 5 [60. 44.21 32.93 27.29 25.41 25.05 25.18 25.98 28.4 33.23 40. ] 4 [60. 42.77 31.29 26.37 25.14 25. 25.06 25.59 27.7 32.62 40. ] 3 [60. 40.86 29.38 25.55 25. 25. 25. 25.23 26.88 31.8 40. ] 2 [60. 38.12 27.19 25. 25. 25. 25. 25. 25.94 30.62 40. ] 1 [60. 33.75 25. 25. 25. 25. 25. 25. 25. 28.75 40. ] 0 [60. 25. 25. 25. 25. 25. 25. 25. 25. 25. 40.] >>>
Se presenta la propuesta del algoritmo EDP parabólicas para el método explícito.
# EDP parabólicas d2u/dx2 = K du/dt # método explícito,usando diferencias divididas import numpy as np # INGRESO # Valores de frontera Ta = 60 # izquierda de barra Tb = 40 # derecha de barra #Tc = 25 # estado inicial de barra en x fxc = lambda x: 25 + 0*x # f(x) en tiempo inicial # dimensiones de la barra a = 0 # longitud en x b = 1 t0 = 0 # tiempo inicial, aumenta con dt en n iteraciones K = 4 # Constante K dx = 0.1 # muestreo en x, tamaño de paso dt = dx/10 n = 100 # iteraciones en tiempo verdigitos = 2 # decimales a mostrar en tabla de resultados # coeficientes de U[x,t]. factores P,Q,R, lamb = dt/(K*dx**2) P = lamb # izquierda P*U[i-1,j] Q = 1 - 2*lamb # centro Q*U[i,j] R = lamb # derecha R*U[i+1,j] # PROCEDIMIENTO # iteraciones en x, longitud xi = np.arange(a,b+dx/2,dx) m = len(xi) ultimox = m-1 ultimot = n-1 # u[xi,tj], tabla de resultados u = np.zeros(shape=(m,n+1), dtype=float) # u[i,j], valores iniciales u[0,:] = Ta # Izquierda u[ultimox,:] = Tb # derecha # estado inicial de barra en x, Tc fic = fxc(xi) # f(x) en tiempo inicial u[1:ultimox,0] = fic[1:ultimox] # Calcula U para cada tiempo + dt tj = np.arange(t0,(n+1)*dt,dt) for j in range(0,n,1): for i in range(1,ultimox,1): # ecuacion discreta, entre [1,ultimox] u[i,j+1] = P*u[i-1,j] + Q*u[i,j] + R*u[i+1,j] # SALIDA j_mostrar = 5 np.set_printoptions(precision=verdigitos) print('Método explícito EDP Parabólica') print('lambda: ',np.around(lamb,verdigitos)) print('x:',xi) print('t:',tj[0:j_mostrar],'...',tj[-1]) print('Tabla de resultados en malla EDP Parabólica') print('j, U[:,:',j_mostrar,'], primeras iteraciones de ',n) for j in range(j_mostrar,-1,-1): print(j,u[:,j])
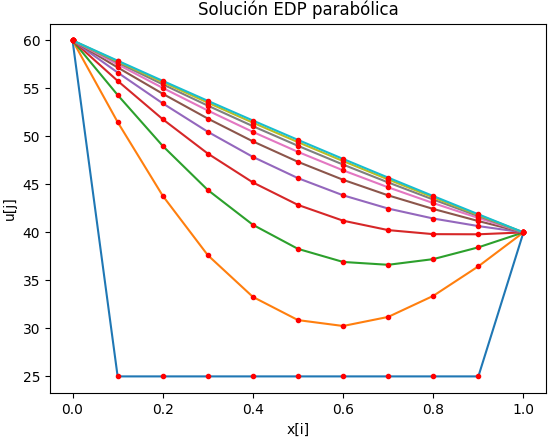
Si la cantidad de puntos aumenta al disminuir Δx y Δt, es mejor disminuir la cantidad de curvas a usar en el gráfico para evitar superponerlas. Se usa el parámetro 'salto' para indicar cada cuántas curvas calculadas se incorporan en la gráfica.
# GRAFICA ------------ import matplotlib.pyplot as plt tramos = 10 salto = int(n/tramos) # evita muchas líneas if (salto == 0): salto = 1 for j in range(0,n,salto): vector = u[:,j] plt.plot(xi,vector) plt.plot(xi,vector, '.',color='red') plt.xlabel('x[i]') plt.ylabel('u[j]') plt.title('Solución EDP parabólica') plt.show()
Note que en la gráfica se toma como coordenadas x vs t, mientras que para la solución de la malla en la matriz las se usan filas y columnas. En la matriz el primer índice es fila y el segundo índice es columna.
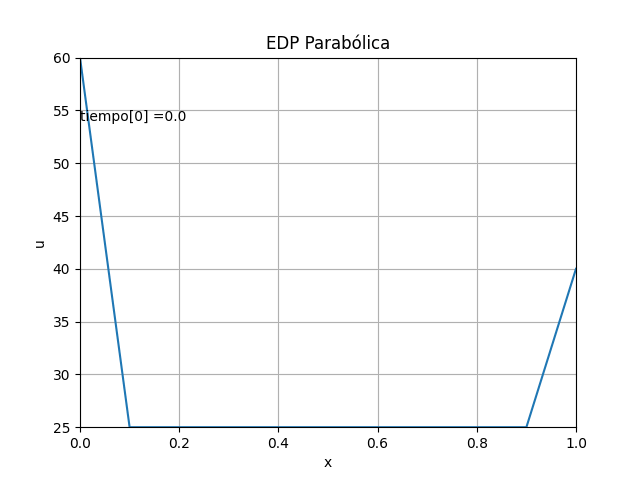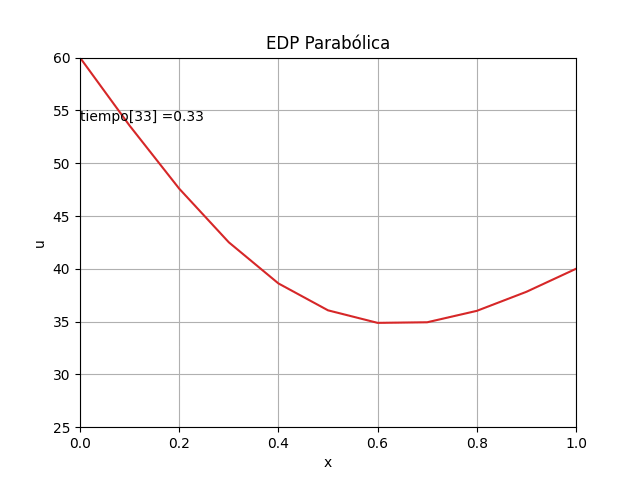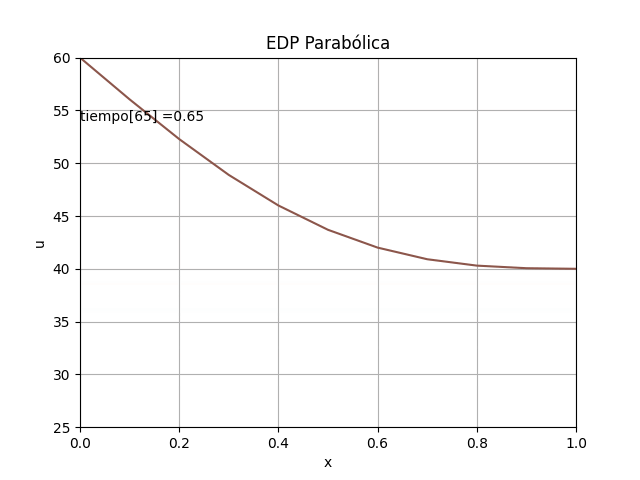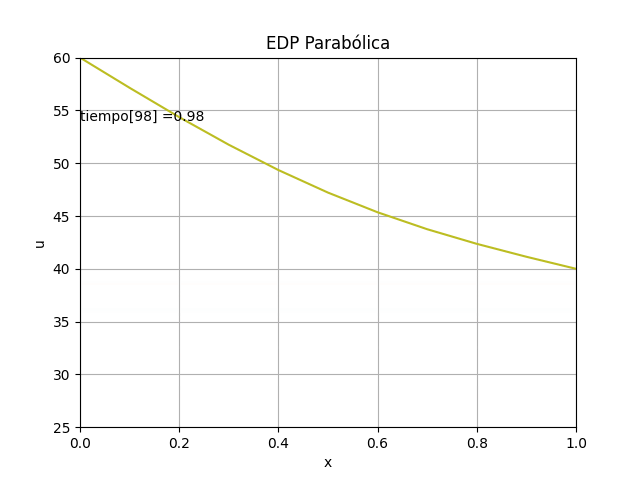
En el caso de una gráfica que se realice usando los ejes x,t,U en tres dimensiones se requiere usar las instrucciones:
# GRAFICA en 3D ------ tj = np.arange(0,n*dt,dt) tk = np.zeros(tramos,dtype=float) # Extrae parte de la matriz U,acorde a los tramos U = np.zeros(shape=(m,tramos),dtype=float) for k in range(0,tramos,1): U[:,k] = u[:,k*salto] tk[k] = tj[k*salto] # Malla para cada eje X,Y Xi, Yi = np.meshgrid(xi,tk) U = np.transpose(U) fig_3D = plt.figure() graf_3D = fig_3D.add_subplot(111, projection='3d') graf_3D.plot_wireframe(Xi,Yi,U, color ='blue') graf_3D.plot(xi[0],tk[1],U[1,0],'o',color ='orange') graf_3D.plot(xi[1],tk[1],U[1,1],'o',color ='green') graf_3D.plot(xi[2],tk[1],U[1,2],'o',color ='green') graf_3D.plot(xi[1],tk[2],U[2,1],'o',color ='salmon', label='U[i,j+1]') graf_3D.set_title('EDP Parabólica') graf_3D.set_xlabel('x') graf_3D.set_ylabel('t') graf_3D.set_zlabel('U') graf_3D.legend() graf_3D.view_init(35, -45) plt.show()
EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]
EDP Parabólica [ concepto ] [ ejercicio ]
Método explícito: [ Analítico ] [ Algoritmo ]