Algoritmos101

Cursos Python

Etiqueta: Ecuaciones Diferenciales Parciales

Ecuaciones Diferenciales Parciales

  • 3Eva_2020PAOII_T3 EDP Deflexiones de una placa

    3ra Evaluación 2020-2021 PAO II. 9/Febrero/2021

    Tema 3. (40 puntos) Una placa cuadrada, apoyada simplemente en sus extremos está sujeta a un carga por unidad de área q.

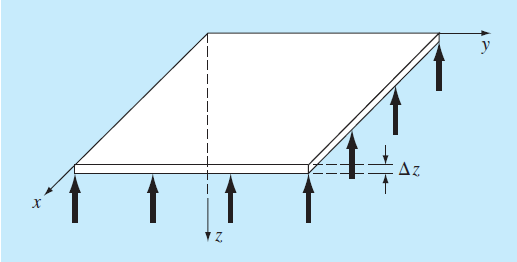
    Deflexion Placa 01
    La deflexión en la dimensión z de determina resolviendo la EDP elíptica siguiente:

    \frac{\partial^4 z}{\partial x^4} + 2\frac{\partial^4 z}{\partial x^2 \partial y^2} +\frac{\partial^4 z}{\partial y^4} =\frac{q}{D}

    sujeta a condiciones de frontera en los extremos, donde la deflexión y la pendiente normal a la frontera son cero.

    D = \frac{E \Delta x^3}{12(1-\sigma ^2)}

    El parámetro D es la rigidez de flexión, donde E=módulo de elasticidad, Δz=espesor de la placa, σ=razón de Poisson.

    Para simplificar, se define la variable u como sigue:

    u = \frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2}

    Permitiendo volver a expresar la ecuación primera como:

    \frac{\partial^2 z}{\partial x^2} + \frac{\partial^2 z}{\partial y^2} = \frac{q}{D}

    Con lo que el problema se reduce a resolver de manera sucesiva las dos ecuaciones de Poisson.

    Primero la ecuación respecto a u sujeta a la condición de frontera u = 0 en los extremos, después los resultados se emplean junto con la ecuación respecto a z sujeta a la condición de que z = 0 en los extremos.
    Considere una placa de 2 metros de longitud en sus extremos, q= 33.6 k N/m2, σ =0.3, Δz = 0.01 m, E = 2x1011 Pa.

    a) Plantee y desarrolle el ejercicio en papel para u(x,y) para al menos 3 puntos en la malla.
    Utilice Δx = Δy = 0.5 para las iteraciones.

    b) Desarrolle un algoritmo para determinar las deflexiones de una placa cuadrada sujeta a una carga constante por unidad de área resolviendo de manera sucesiva las dos ecuaciones.

    Rúbrica: gráfica de malla (5 puntos), desarrollo de expresiones, agrupar constantes, y simplificación (10 puntos), iteraciones para 3 puntos (10 puntos), Revisión de errores (5 puntos). literal b (10 puntos)

    Referencia: Deflexiones de una placa. Chapra 32.2 p938, pdf962

  • 3Eva_2020PAOI_T3 EDP Parabólica

    3ra Evaluación 2020-2021 PAO I. 22/Septiembre/2020

    Tema 3. (35 puntos) Desarrolle con el método implícito para aproximar la solución de la EDP Parabólica

    \frac{\partial u}{\partial t} - c^2 \frac{\partial ^2 u}{\partial x^2} = g(x)
    u(x,0) = f(x) u(0,t) = 0 u(1,t) = 0
    f(x) = \begin{cases} 5x , & 0 \le x \le 0.5 \\ 5(1-x) , & 0.5 \lt x \le 1\end{cases} g(x) = 2 , 0 \le x \le 1

    Considere para h=0.25, k=0.05, c=1

    a. Grafique la malla
    b. Escriba las ecuaciones para las derivadas
    c. Plantee las ecuaciones
    d. Resuelva para tres pasos
    e. Estime el error (solo plantear)

    Rúbrica: literal a (5 puntos), literal b (5puntos), literal c (10 puntos), literal d (10 puntos), literal e (5 puntos)

  • 2Eva_IIT2019_T3 EDP elíptica, placa en (1,1)

    2da Evaluación II Término 2019-2020. 28/Enero/2020. MATG1013

    Tema 3. (30 Puntos) Para la ecuación diferencial parcial elíptica mostrada:

    \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = \frac{x}{y} + \frac{y}{x}

    1 <  x < 2
    1 <  y < 2

    Y con las siguientes condicines de frontera:

    u(x,1)= x \ln (x), u(x,2) = x \ln (4x^{2}),1 \lt x \lt 2 u(1,y)= y \ln(y), u(2,y) = 2y \ln (2y), 1 \lt y \lt 2

    Considere los valores hx=hy=0.25

    Realice la aproximación numérica para la solución.

    Para resolver el sistema de ecuaciones utilice el método de Gauss-Seidel para dos iteraciones.

    Rúbrica: Plantear la malla (5 puntos), calcular los bordes (3 puntos), plantear las segundas derivadas (7 puntos), plantear las ecuaciones  (10 puntos), aproximar la solución  (5 puntos)

  • 3Eva_IT2019_T3 EDP Difusión en sólidos

    3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

    Tema 3. (30 Puntos).  En el año 1855, los experimentos de Adolf Fick tratan sobre la medición de concentraciones y sus flujos, también ahora aplicados a la difusión en sólidos que en ese tiempo no se consideraba posible.

    Difusion En Solidos 01

    La gráfica muestra los cambios en el tiempo de concentración Φ de un gas en un sólido (estado no-estacionario) para un sólido semi infinito (eje y).

    La segunda ley de Fick predice la forma en que la difusión causa que la concentración cambie con el tiempo. Se trata de una ecuación diferencial parcial que en una dimensión se escribe:

    \frac{\partial \phi}{\partial t} = D\frac{\partial ^2 \phi}{\partial x^2}
    Φ(0, t) = 5
    Φ(L, t) = 0
    Φ(x,0) = 0    		 D = 0.16
    L =0.1

    a. Plantee las ecuaciones, la malla, desarrolle y obtenga el modelo Φ(xi,tj)

    b. Aproxime la solución con Δx = 0.02, Δt = Δx/100. Realice al menos tres iteraciones en el eje tiempo.

    c. Estime el error de Φ(xi,tj)

    Rúbrica: Construir la malla (5 puntos), plantear la ecuación en el nodo i,j (5 puntos), modelo de ecuación (5 puntos), literal b (10 puntos), literal c (5 puntos).

    Referencia: https://es.wikipedia.org/wiki/Leyes_de_Fick;
    Difusión 2ª Ley de Fick|7/22|UPV (2011) https://www.youtube.com/watch?v=HHBvZDNvTic

  • 2Eva_IT2019_T3 EDP Elíptica Placa 6x5

    2da Evaluación I Término 2019-2020. 27/Agosto/2019. MATG1013

    Tema 3. (30 Puntos) Una placa rectangular de plata de 6x5 cm tiene calor que se genera uniformemente en todos los puntos, con una rapidez q = 1.5 cal/cm3 s.

    Al representar con x la distancia a lo largo del borde de longitud 6 cm y con y la de 5 cm.

    Suponga que la temperatura en los bordes se mantiene como se indica:

    u(x,0) = x(6-x) u(x,5)=0 0≤x≤6
    u(0,y) = y(5-y) u(6,y)=0 0≤y≤5

    Donde el origen se encuentra en una esquina de la placa y los bordes se hayan a lo largo de los ejes positivos x, y.

    La temperatura de estado estable u(x,y) satisface la ecuación de Poisson:

    \frac{\partial^2 u}{\partial x^2} (x,y)+\frac{\partial ^2 u}{\partial y^2 } (x,y) = -\frac{q}{K}

    0≤x≤6
    0≤y≤5

    Donde K, la conductividad térmica es 1.04 cal/cm deg s.

    a. Aproxime la temperatura u(x,y) en los nodos de la malla con hx =2, hy= 2.5

    b. Exprese el término del error

    Rúbrica: literal a expresiones (10 puntos), valor (10 puntos), literal b (5 puntos)

    Referencia: Ejercicio 12.1.8, Burden 9Ed, p724.

  • 2Eva_IIT2018_T3 EDP

    2da Evaluación II Término 2018-2019. 29/Enero/2019. MATG1013

    Tema 3. (40 puntos) Resuelva la siguiente ecuación diferencial parcial (EDP) usando un método de diferencias finitas. Considere b = 0

    \frac{\partial u}{\partial t} = \frac{\partial ^2 u}{\partial x^2} + b\frac{\partial u}{\partial x} 0<x<1, t>0

    condiciones de frontera U(0,t)=0, U(1,t)=1

    condiciones de inicio U(x,0)=0, 0≤x≤1

    a) Aproxime la solución con h=0.25, realice dos pasos en t

    b) estime el error.

    Rúbrica: Plantea la malla (5 puntos), Conoce las fórmulas de las derivadas (5 puntos), Plantea la ecuación en los nodos de la malla (5 puntos), plantea las condiciones iniciales y condiciones de borde (5 puntos), Establece el valor de lamda y calcula el tamaño del paso k, (5 puntos) Realiza dos pasos (5 puntos), Conoce las fórmulas del error (5 puntos), calcula el error (5 puntos).

  • 3Eva_IT2018_T3 EDP Parabólica, temperatura en varilla

    3ra Evaluación I Término 2018-2019. 11/Septiembre/2018. MATG1013

    Tema 3. (30 puntos) La temperatura u(x,t) de una varilla larga y delgada, de sección transversal constante y de un material conductor homogéneo está regida por la ecuación unidimensional de calor. Si se genera calor en el material (por ejemplo, debido a la resistencia de la corriente), la ecuación se convierte en:

    \frac{\partial ^2u}{\partial x^2} + \frac{Kr}{\rho C} = K\frac{\partial u}{\partial t} 0 \lt x \lt L, 0 \lt t
    Donde: Suponga que:
    L es la longitud, L =  1.5 cm
    ρ es la densidad, ρ = 10.6 g/cm3
    C es el calor específico C = 0.056 cal/g deg
    K es la difusividad térmica de la varilla K = 1.04 cal/cm deg s
    La función r = r(x,t,u) representa el calor generado por unidad de volumen. r(x,t,u) = 5 cal/g deg

    Si los extremos de la varilla se mantienen a 0°C, entonces

    u(0,t) = u(L,t) = 0, t>0

    Suponga que la distribución inicial de la temperatura está dada por:

    u(x,0) = \sin \Big( \frac{\pi x}{L} \Big), 0 \le x \le L

    Aproxime la distribución de la temperatura con h=0.25, k=0.025 para t=3k

    Referencia: Burden 9ed Chapter 12 exercise 18 p738

  • 2Eva_IT2018_T3 EDP Eliptica

    2da Evaluación I Término 2018-2019. 28/Agosto/2018. MATG1013

    Tema 3. (25 puntos) Considere el problema con valores en la frontera:

    \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = 2(x^2+y^2) 0<x<1 0<y<1

    con las condiciones de frontera en los mismos intervalos que la ecuacion diferencial:

    u(x,0) = x + 1 u(0,y) = y+1 u(x,1) = x^2 + x +2 u(1,y) = y^2 + y +2

    Use el método de diferencias finitas para resolver el problema tomando como tamaño de paso hx = hy = 1/3

    Rúbrica: Selección de diferencias finitas divididas, gráfica del problema (5 puntos), ecuación generalizada con diferencias finitas divididas (5 puntos), Sistema de ecuaciones para los puntos desconocidos (10 puntos). Valores de los puntos desconocidos (5 puntos)

     

  • 3Eva_IIT2017_T3 EDP Elíptica, placa rectangular

    3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

    Tema 3. Aproxime la solución de la siguiente EDP elíptica.

    \frac{\partial^2 u}{\partial x^2} + \frac{\partial ^2u}{\partial y^2} = (x^2 + y^2) e^{xy} 0 \lt x \lt 2, 0 \lt y \lt 1

    con condiciones de frontera

    u(0,y) = 1 , u(2,y) = e^{2y}, 0 \leq y \leq 1 u(x,0) = 1, u(x,1) = e^x , 0 \leq x \leq 2

    a) use tamaños de paso h = 2/3 y k = 1/3

    b) compare con la solución u(x,y) = exy en forma gráfica

  • 2Eva_IIT2017_T3 EDP parabólica con diferencias regresivas

    2da Evaluación II Término 2017-2018. Febrero 7, 2018. MATG1013

    Tema 3. Aproxime la solución de la sigiente EDP parcial usando diferencias regresivas

    \frac{\partial U}{ \partial t} - \frac{1}{16} \frac{\partial ^2U}{\partial x^2} = 0 0 \lt x \lt 1 , 0\lt t U(0,t) = U(1,t) = 0, 0\lt t, U(x,0) = 2 \sin (\pi x), 0\leq x \leq 1

    a) Plantee las ecuaciones usando hx = 1/3, ht = 0.05, T = 2

    b) Calcule U(xi,tj)

    c) Plantee el error de U(xi,tj)