Algoritmos101

Cursos Python

Etiqueta: integración numérica

Integración Numérica

  • 3Eva_2021PAOII_T1 Area con derrame de petroleo usando Simpson

    3ra Evaluación 2021-2022 PAO II. 8/Febrero/2022

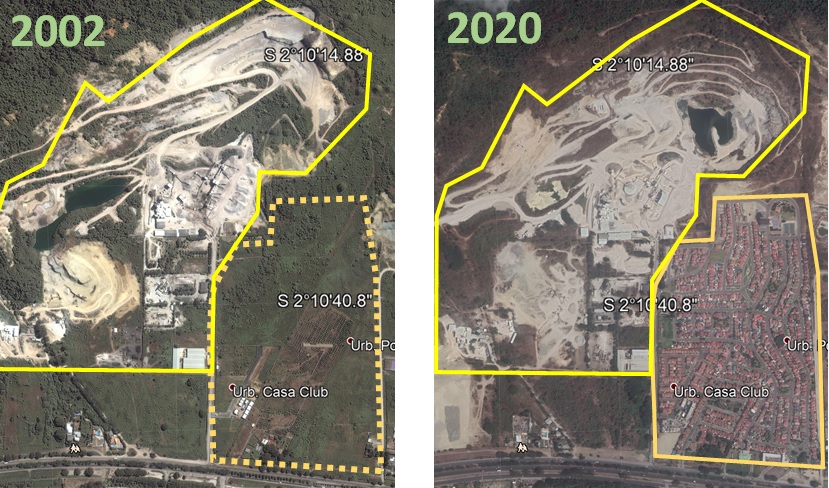
    Tema 1. (30 puntos) Se reportó un derrame de petróleo del pasado 15 de enero del 2022 en una refinería en el vecino país del sur, Derrame Petroleo 02
    que contaminó al menos 24 playas de la costa central, según indicó el organismo de la Dirección General de Salud Ambiental e Inocuidad Alimentaria.

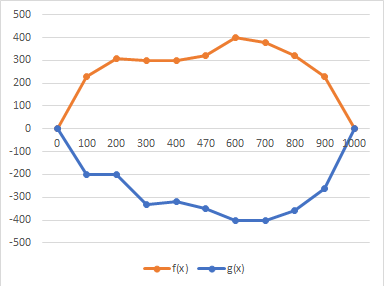
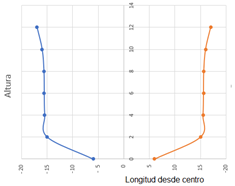
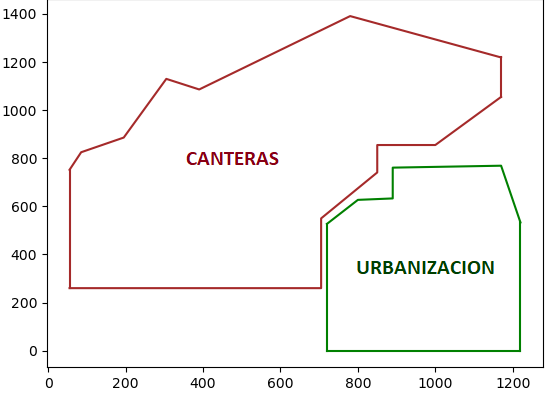
    Usando fotografías aéreas, la guardia costera obtuvo las dimensiones del derrame descrita en la figura y en la tabla mostrada:

    Derrame Petroleo 01

    x 0 100 200 300 400 470 600 700 800 900 1000
    f(x) 0 230 310 300 300 320 400 380 320 230 0
    g(x) 0 -200 -200 -330 -320 -350 -400 -400 -360 -260 0

    a) Estime el área afectada por el derrame de petróleo, usando principalmente los métodos Simpson
    b) Justifique el uso de las formulas compuestas usadas
    c) Calcule el error del integral, para toda el área

    Rúbrica: literal b (5 puntos), literal a, con expresiones detalladas para cada eje (20 puntos), literal c (5 puntos)

    Referencia: Tan S.T (1994). Numerical Integration 7.3 Ejercicio 5. Calculus for the managerial, life, and Social sciences.
    Eluniverso.com Derrames de petróleo, una lamentable afectación que es habitual a la región. 31 de enero, 2022. https://www.eluniverso.com/noticias/internacional/derrames-de-petroleo-una-lamentable-afectacion-que-es-habitual-a-la-region-nota/

    x  = [0.0, 100, 200, 300, 400, 470, 600, 700, 800, 900, 1000]
fx = [0.0, 230, 310, 300, 300, 320, 400, 380, 320, 230, 0]
gx = [0.0,-200,-200,-330,-320,-350,-400,-400,-360,-260, 0]

     

  • 2Eva_2021PAOII_T1 Promedio de precipitación de lluvia en área

    2da Evaluación 2021-2022 PAO II. 25/Enero/2022

    Tema 1 (30 puntos) Un mapa asociado al clima muestra los resultados de precipitación que dejó a su paso el Huracán Karl en el año 2010.

    Se registró entre 4 a 8 pulgadas de lluvia. El área en observación tiene una extensión de 300 millas de este a oeste y 250 millas de norte a sur.

    f(xi,yj)
    i \ j 1 2 3 4 5 6
    1 0.02 0.36 0.82 0.65 1.7 1.52
    2 3.15 3.57 6.25 5 3.88 1.8
    3 0.98 0.98 2.4 1.83 0.04 0.01
    4 0.4 0.04 0.03 0.03 0.01 0.08

    Para las mediciones, se divide el área del mapa en 6 tramos para el eje x, 4 tramos para el eje y, con lo que se encuentran los valores presentados en la tabla.

    a) Determine los valores para Δx, Δy.

    b) Estime al promedio de precipitación lluviosa en toda el área para los datos registrados para dos días, usando la forma compuesta de Simpson.

    f_{promedio} = \frac{1}{A_R} \int \int_R f(x,y) \delta x \delta y

    c) Calcule el error del integral

    Rúbrica: literal a (5 puntos), literal b, con expresiones detalladas para cada eje (20 puntos), literal d (5 puntos)

    Referencia: Stewart. Calculus Example 15.1.10: Calculating Average Storm Rainfall.

    A = [[0.02, 0.36, 0.82, 0.65, 1.7 , 1.52],
     [3.15, 3.57, 6.25, 5.  , 3.88, 1.8 ],
     [0.98, 0.98, 2.4 , 1.83, 0.04, 0.01],
     [0.4 , 0.04, 0.03, 0.03, 0.01, 0.08]]
base = 300
altura = 250

  • 3Eva_2021PAOI_T4 Integral con Cuadratura Gaussiana

    3ra Evaluación 2021-2022 PAO I. 14/Septiembre/2021

    Tema 4 (30 puntos) Aproximar el siguiente integral usando Cuadratura Gaussiana

    \int_0^{\pi/4} x^2 \sin (x) \delta x

    a) Usado dos segmentos o tramos, y para dos puntos, n=2

    b) compare sus resultados con n=3

    c) Calcule error entre resultados

    Referencia: Burden 8th Edition. Ejercicios 4.7 d.

    Rúbrica: Planteo del ejercicio (5 puntos), literal a, con expresiones y valores completos (10 puntos), literal b, con n=3 (10 puntos). literal c (5 puntos).

  • 2Eva_2021PAOI_T1 Masa transportada por tubo

    2da Evaluación 2021-2022 PAO I. 31/Agosto/2021

    Tema 1 (30 puntos) La cantidad de masa transportada, M, por un tubo durante cierto periodo de tiempo se calcula con: plataforma Submarina 01

    M = \int_{t_1}^{t_2} Q(t)c(t) dt

    Donde:
    M = masa (mg)
    t1 = tiempo inicial (min)
    t2 = tiempo final (min)
    Q(t) = tasa de flujo (m3/min)
    c(t) = concentración (mg/m3)

    Las representaciones funcionales siguientes definen las variaciones temporales en el flujo y la concentración:

    Q(t)=9+4 \cos ^2 (0.4t) c(t)=5e^{-0.5t}+2 e^{-0.15 t}

    a) Determine la masa transportada entre t1 = 2 min y t2 = 8 min, usando integración numérica de Simpson 1/3 con al menos 6 tramos.

    b) Estime la cota de error para el literal anterior.

    c) Recomiende y justifique cómo mejorar el resultado de lo calculado de forma numérica.

    Rúbrica: Planteamiento (5 puntos), iteración con expresiones completas (10 puntos), tamaño de paso (5 puntos), cota error (5 puntos), literal c (5 puntos)

    Referencia: Chapra ejercicio 22.14 p667. ¿Cómo funciona una refinería? https://youtu.be/tFJ064TLW4E
    ¿Cómo lo hacen? - Extracción de petróleo - DiscoveryMAX en Español https://youtu.be/ua8u3iSFqsc

  • 3Eva_2020PAOII_T1 Área de sección transversal en buque

    3ra Evaluación 2020-2021 PAO II. 9/Febrero/2021

    Tema 1. (30 puntos) Al reiniciar las actividades de construcción de un buque
    luego de la cuarentena del año 2020, se requiere determinar el área transversal de la sección a ser cerrada completamente y que se muestra en la figura.

    Para estimar el área transversal del compartimento se tomaron las siguientes medidas cada 2 metros hacia arriba desde la línea central vertical (mostrada en la gráfica):

    en metros Longitud desde Centro
    Altura Izquierda Derecha
    12 -17.00 17.00
    10 -16.00 16.00
    8 -15.65 15.65
    6 -15.60 15.60
    4 -15.50 15.50
    2 -15.00 15.00
    0   -6.00  6.00

    Usando un método numérico compuesto estime el área transversal de la sección del barco y la cota de error del ejercicio. Desarrolle el ejercicio mostrando el método seleccionado, las expresiones en la ecuación con los valores usados y el error total.

    Rúbrica: Selección del métodos compuestos (5 puntos), expresiones de áreas (10 puntos), cota de errores (10 puntos), área total (5 puntos)

    tabla = [[0.0,  2.0,  4.00,  6.00,  8.00, 10.0, 12.0],
         [6.0, 15.0, 15.50, 15.60, 15.65, 16.0, 17.0]]

    Referencias: Órdenes de construcción de transporte marítimo disminuyo en abril. 2020-05-10. https://www.worldenergytrade.com/logistica/transporte/ordenes-de-construccion-de-transporte-maritimo-disminuyo-abril

     

  • 3Eva_IIT2019_T3 Preparación de terreno en refineria

    3ra Evaluación II Término 2019-2020. 11/Febrero/2020. MATG1013

    Tema 3. (25 puntos) Para valorar la preparación de terreno en una planta procesadora de Refinería, se requiere estimar el volumen de remoción.

    preparación de terreno

    Para una sección rectangular, se dispone de las alturas sobre el nivel del mar del terreno en una cuadrícula antes de los trabajos, siendo el nivel requerido de 220 m en toda el área.

    Nivel inicio (m) 0 50 100 150 200
    0 241 239 238 236 234
    25 241 239 237 235 233
    50 241 239 236 234 231
    75 242 239 236 232 229
    100 243 239 235 231 227

    Usando los métodos de integración numérica determine el volumen de material para ésta actividad.

    a) Determine el volumen de remoción

    b) Exprese y determine el error de aproximación para el volumen

    Rúbrica: literal a (15 puntos), literal b (10 puntos)

    Referencias: Liquidar Refinería del Pacífico tardaría años. 27 de enero, 2020. www.eluniverso.com.
    https://www.eluniverso.com/noticias/2020/01/27/nota/7710855/refineria-pacifico-liquidacion-rafael-correa-activos-ministerio
    Inicia liquidación de la Refinería del Pacífico. 16-03-2019. vistazo.com.
    https://www.vistazo.com/seccion/politica-nacional/inicia-liquidacion-de-la-refineria-del-pacifico

    # INGRESO
nInicio = np.array([[241, 239, 238, 236, 234],
                    [241, 239, 237, 235, 233],
                    [241, 239, 236, 234, 231],
                    [242, 239, 236, 232, 229],
                    [243, 239, 235, 231, 227]])

nRequerido = 220

xi = np.array([0,50,100,150,200])
yi = np.array([0,25,50,75,100])

hx = 50
hy = 25

  • 2Eva_IIT2019_T4 Integrar con Cuadratura de Gauss

    2da Evaluación II Término 2019-2020. 28/Enero/2020. MATG1013

    Tema 3. (25 Puntos) Considere la función f con regla de correspondencia:

    f(x) = x ln(x)

    Se desea aproximar el valor del integral I en el intervalo [1,4]

    I = \int_a^b f(x) dx

    a) Use el método de Cuadratura de Gauss con 2 términos para aproximar el valor de I en el intervalo [1,4]

    Usando el método compuesto de Simpson:

    I = I_s - \frac{(b-a)}{180}h^4 f^{(4)} (\xi) ; \xi \in[a,b]

    Donde Is es el valor aproximado de I y h la longitud de cada intervalo.

    b) Determine el mínimo número de subintervalos que permita alcanzar una tolerancia de 0.0001. NO considere errores de redondeo.

    Rúbrica: literal a (10 puntos), literal b (15 puntos)

  • 2Eva_IIT2019_T1 Canteras y urbanizaciones

    2da Evaluación II Término 2019-2020. 28/Enero/2020. MATG1013

    Tema 1. (20 Puntos) En el conflicto presentado entre las urbanizaciones y canteras en vía a la costa, se menciona que se ha afectado al ecosistema al disminuir la vegetación en la zona.

    Una forma de observar el cambio en la zona es medir el área ocupada por cada actor.

    Cantera Urbaniza 01

    Para la observación considere que la superficie ocupada por las urbanizaciones y canteras se describe con los siguientes datos de frontera:

    Cantera Urbaniza 02

    Canteras- frontera superior
    xi 55 85 195 305 390 780 1170
    f(xi) 752 825 886 1130 1086 1391 1219
    Canteras- frontera inferior
    xi 55 ... 705 705 850 850 1010 1170
    f(xi) 260 ... 260 550 741 855 855 1055
    Urbanización - frontera superior
    xi 720 800 890 890 1170 1220
    g(xi) 527 630 630 760 760 533
    Urbanización - frontera inferior
    xi 720 ... 1220
    g(xi) 0 ... 0

    Nota: Observe que los tamaños de paso no son todos regulares

    Usando el método del trapecio, determine:

    a) El área de operación de la cantera

    b) El área ocupada por la urbanización

    c) ¿Se puede mejorar la precisión del cálculo de las áreas, sin quitar o aumentar datos? Justifique su respuesta e indique cómo y dónde.

    Rúbrica: literal a (5 puntos), literal b(5 puntos), literal c: cómo (5 puntos), dónde(5 puntos)

    Referencia: Google Maps Enero 2019.
    Dos bosques cercados por el crecimiento de Guayaquil. 27- Julio-2014.
    https://www.eluniverso.com/noticias/2014/07/27/nota/3282036/dos-bosques-cercados-urbe-que-crece
    La remediación ambiental en vía a la costa tomará giro legal. 02-Enero-2020.
    https://www.expreso.ec/guayaquil/remediacion-ambiental-via-costa-tomara-giro-legal-2518.html

  • 3Eva_IT2019_T2 Integral con interpolación

    3ra Evaluación I Término 2019-2020. 10/Septiembre/2019. MATG1013

    Tema 2. (40 Puntos) Construya un polinomio que aproxime a

    f(x) = sin(\pi x)

    usando los puntos x=0, π/4, π/2 y aproxime la integral de 0 a π/2.

    a. Realice la interpolación mediante el método de trazador cúbico fijo

    b. Integre usando el método de cuadratura de Gauss

    c. Estime el error para el ejercicio.

    Rúbrica: Bosquejo de gráficas (5 puntos), literal a, planteo de fórmulas (5 puntos), calcula los parámetros (10 puntos), literal b (15 puntos), literal c (5 puntos).

  • 2Eva_IT2019_T1 Esfuerzo en pulso cardiaco

    2da Evaluación I Término 2019-2020. 27/Agosto/2019. MATG1013

    Tema 1. (30 Puntos) La conducción eléctrica del corazón se identifica en un electrocardiograma por segmentos de ondas P, R, T.

    Pulso Cardiaco EKG 01Mediante un sensor se obtuvo lecturas de un pulso cardiaco y se requiere obtener una medida del esfuerzo mediante el valor Xrms expresado como:

    X_{rms} = \sqrt{\frac{1}{t_n-t_0}\int_{t_0}^{t_n}[f(t)]^2dt}
    t 0.0 0.04 0.08 0.1 0.11 0.12 0.13 0.16 0.20 0.23 0.25
    f(t) 10 18 7 -8 110 -25 9 8 25 9 9

    a. Aproxime el valor Xrms usando el integral en todo el intervalo [0,0.25], minimice el error usando preferiblemente métodos de Simpson.

    b. Estime la cota de error para el valor Xrms encontrado
    Justifique sus respuestas escribiendo todas las expresiones

    Rúbrica: literal a, expresiones (16 puntos), valor (8 puntos), literal b (6 puntos)

    t  = np.array([0.0,0.04,0.08,0.1,0.11,0.12,0.13,0.16,0.20,0.23,0.25])
ft = np.array([10.0, 18, 7, -8, 110, -25, 9, 8, 25, 9, 9])

    Referencia: Valor cuadrático medio, https://es.wikipedia.org/wiki/Media_cuadr%C3%A1tica
    Sensor de pulso cardiaco arduino, http://blog.espol.edu.ec/edelros/pulso-cardiaco/