Etiqueta: interpolación polinómica

1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158

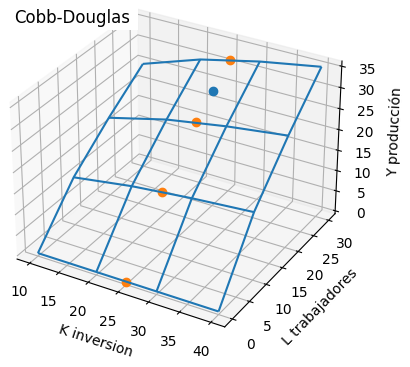
Tema 2. La función de producción llamada Cobb-Douglas relaciona funcionalmente a los insumos de capital y trabajo necesarios para producir de la manera más óptima de una determinada cantidad de un bien.

Y = f(K,L) es la cantidad máxima del bien que se puede producir dados los insumos utilizados de capital y trabajo. K y L representan las cantidades de capital y trabajo respectivamente.

En la industria de lácteos se han observado los siguientes valores óptimos de producción Y (en miles de Kg) para diferentes valores de L (número de trabajadores)  y capital invertido K (en miles de dólares).

L\K (miles $)	10	20	30	40
0	0	0	0	0
10	11.0000	13.0813	14.4768	15.5563
20	18.4997	22.0000	24.3470	26.1626
30	25.0746	29.8189	33.0000	35.4608

a. Determinar usando el polinomio de interpolación de Lagrange,

¿cuál será la producción óptima de lácteos en una empresa que emplea 25 trabajadores y que invierte un capital de $ 25000 en el plan de producción?

 

b.  Una empresa que tiene 25 trabajadores desea producir 30000 Kg de lácteos. ¿cuánto dinero deberá invertir?, use el polinomio de interpolación y el método de Newton-Raphson con una precisión de 10^-5

---

a.1 Plantear y Desarrollar las expresiones de al menos dos polinomios de Lagrange por filas de la tabla. Los demás puede completar con el algoritmo.

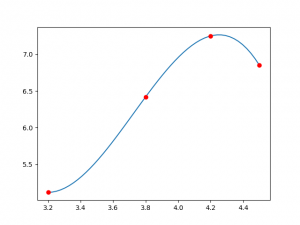
a.2 Use el resultado de cada polinomio para evaluar con K=25. Con los datos de la columna K=25, genere un nuevo polinomio p_(K=25)(L) para usarlo para encontrar el valor de Y con L=25.

b.1 Realice el planteamiento del ejercicio,  para L= 25, es decir ahora por columnas y obtenga el polinomio p_(L=25)(K).

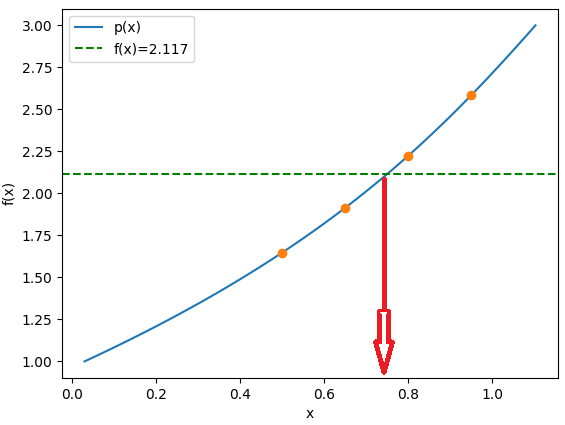
b.2 Plantear usando el polinomio Y(K) = p_(L=25)(K) con el método de Newton-Raphson, que encuentre el valor de inversión K para una producción Y.

b.3 Desarrolle las expresiones para tres iteraciones.

b.4 Analice la convergencia del método.

Adjunte sus algoritmos.py, resultados.txt y gráficas.png.

Rúbrica: literal a.1 (10 puntos), literal a.2 (5 puntos)m literal b.1 (5 puntos), b.2(5 puntos), b.3 (5 puntos)

Referencia: Wikipedia/Cobb-Douglas

# INGRESO
M = [[ 0,       0,       0,       0     ],
     [11.0000, 13.0813, 14.4768, 15.5563],
     [18.4997, 22.0000, 24.3470, 26.1626],
     [25.0746, 29.8189, 33.0000, 35.4608]]
li = [0, 10, 20, 30]
kj = [10, 20, 30, 40]

l_busca = 25 # trabajadores
k_busca = 25 # inversion en miles de $

1ra Evaluación II Término 2007-2008. 4/Diciembre/2007.
ICM00158

Tema 3. Dado los datos de una función:

f(0.50) = 1.648
f(0.65) = 1.915
f( x  ) = 2.117
f(0.80) = 2.225
f(0.95) = 2.5857

Determinar el valor de x, usando interpolación inversa.

---

xi = [0.50 , 0.65 , x, 0.80 , 0.95  ]
fi = [1.648, 1.915, 2.117, 2.225, 2.5857]

a. Plantear el ejercicio describiendo los criterios a usar para el polinomios para el eje y.

b. Desarrolle el método sobre los puntos seleccionados con las expresiones completas desarrolladas con el algoritmo.

c. Presentar el polinomio resultante y la gráfica usando la resolución requerida para el estudio.

d. Adjunte los archivos: algoritmos.py, resultados.txt y gráfica.png del polinomio.

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos), literal d (5 puntos).