1ra Evaluación I Término 2019-2020. 2/Julio/2019. MATG1013

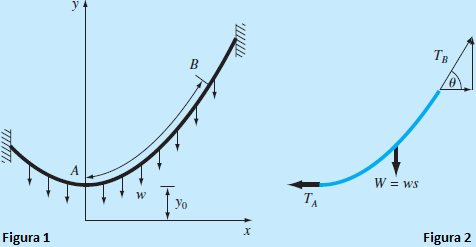
Tema 2. (30 puntos) Un cable en forma catenaria es aquel que cuelga entre dos puntos que no se encuentran sobre la misma línea vertical. Como se muestra en la figura 1, no está sujeta a más carga que su propio peso. Así, su peso en N/m actúa como una carga uniforme por unidad de longitud a lo largo del cable.

En la figura 2, se ilustra un diagrama de cuerpo libre de una sección AB, donde T_A y T_B son las fuerzas de tensión en el extremo.

Con base en los balances de fuerzas horizontal y vertical, se obtiene para el cable el siguiente modelo:

y = \frac{T_A}{w} cosh \Big( \frac{w}{T_A}x \Big) + y_0 - \frac{T_A}{w}

Donde la altura y del cable está en función de la distancia x.

Además se tiene que:

cosh(z) = \frac{e^z+ e^{-z}}{2}

Utilice el método de Newton-Raphson para hallar el valor del parámetro T_A dado los valores de los parámetros w=12, y₀=6 de modelo que el cable tenga una altura de 15 metros para x=50

Rúbrica: Planteamiento del problema (10 puntos), obtener la derivada (5 puntos), plantear el método (5 puntos), iteraciones (5 puntos), verificar tolerancia (5 puntos)

---

Nota: Todos los temas deben mostrar evidencia del desarrollo del método numérico planteado.

Referencia: Chapra 5Ed Problema 8.17 p219 pdf243. Sears&Zemanski Vol1 12Ed problema 5.63. Cuerda con masa p173. https://es.wikipedia.org/wiki/Catenaria

1ra Evaluación II Término 2018-2019. 10/Noviembre/2018. MATG1013

Tema 4. Para pagar una hipoteca de una casa durante n periodos de tiempo se usa la fórmula:

P = A\Big(\frac{1-(1+i)^{-n}}{i} \Big)

En ésta ecuación, P es el valor presente de la casa, A es el valor del pago periódico de la deuda durante n periodos y la tasa de interés por periodo es i.

Suponga que la casa tiene un valor presente de 70000 dólares y deberá ser pagada mediante 1200 dólares mensuales por 25 años (300 meses).

a) Plantee la ecuación

b) Encuentre un intervalo para i donde haya un cambio de signo en la función

c) Aplique el método de Newton

1ra Evaluación II Término 2018-2019. 10/Noviembre/2018. MATG1013

Tema 2. Aproxime con un grado de exactitud de 0.0001 el valor de x que en la gráfica de y=e^x está más cerca al punto P(1,1).

a) Plantear la ecuación

b) Hallar un intervalo de existencia y de convergencia

---

Referencias: 

Gigante asteroide con su propia Luna pasará en cercanías de la Tierra . https://www.eluniverso.com/noticias/2019/05/23/nota/7344362/gigante-asteroide-su-propia-luna-pasara-cercanias-tierra

 Un asteroide dos veces más grande que un avión Boeing 747 pasará muy cerca la Tierra. https://www.eluniverso.com/noticias/2018/08/28/nota/6927335/asteroide-dos-veces-mas-grande-que-avion-pasara-muy-cerca-tierra

 

Referencia: https://spaceplace.nasa.gov/comet-quest/sp/

1ra Evaluación I Término 2018-2019. 26/junio/2018. MATG1013

Tema 2. (25 puntos) Sea g:[a,b] → R una función continua tal que g(x) ∈ [a,b] para toda x ∈ [a,b] .
Suponga además que g es una función contractiva en [a,b] esto es
\forall x,y \in [a,b]: |g(x)-g(y)| \lt |x-y|

Demuestre o refute las siguientes afirmaciones:

a) g tiene al menos un punto fijo en [a,b]

b) g tiene un punto fijo único en [a,b]

Rúbrica:
Literal a. Construye la función f(x)=x-g(x)=0 , verifica el cambio de signo de f(x) en los extremos del intervalo y concluye que p =g(p) (hasta 15 puntos),
literal b. Supone dos puntos fijos, calcula | p-q |, utiliza la propiedad contractiva y concluye que se produce una contradicción (hasta 10 puntos)

3ra Evaluación II Término 2017-2018. Febrero 20, 2018. MATG1013

Tema 1. Sea g: [a,b] →ℜe (reales) una función diferenciable tal que g(x) ∈ [a,b], para toda x ∈ [a,b]. Demuestre o refute las siguientes afirmaciones.

a) g tiene al menos un punto fijo en [a,b]

b) g tiene un punto fijo único en [a,b]

3ra Evaluación II Término 2011-2012. 14/Febrero/2012. ICM02188 Métodos Numéricos

Tema 1. (30 puntos) Suponga que el precio de un producto f(x) depende del tiempo x en el que se lo ofrece al mercado con la siguiente relacion:

f(x) = 25x e^{-0.1x} 0\leq x \leq 12

en donde x es tiempo en meses.

Se desea determinar el dia en el que el precio sube a 80.

a. Evalúe f con x en meses hasta que localice una raíz real (cambio de signo) y trace la forma aproximada de f(x)

b. Use el Método de Newton-Raphson para calcular la respuesta (mes) con precisión 10^-4. Exprese esta respuesta en días (1mes = 30 días)

c. Encuentre el día en el cual el precio será máximo. Use el método de Newton con precisión 10^-4

3ra Evaluación I Término 2010-2011. 14/Septiembre/2010. ICM00158

Tema 1. Un envase de lata con forma de cilindro circular recto, será construido para contener 1000 cm³.

Las partes superior e inferior circulares del envase deben tener un radio de 0.25 mayor que el radio de éste, de manera que el excedente pueda usarse para formar un sello con el cuerpo principal.

La hoja de material con la que se forme dicho cuerpo, debe ser también de 0.25 cm más larga que la circunferencia del envase, de manera que se pueda formar un sello.

Encuentre con un error de 10^-4 la cantidad mínima de material para construir dicha lata.

---

Referencias: Burden Cap2.6 Ejercicio 11 9Ed p101

 

3ra Evaluación II Término 2008-2009. 3/Marzo/2009. ICM00158

Tema 4. Con los conocimientos de cálculo diferencial y geometría analítica, deduzca el método de Newton para determinar las raíces de una función .

Luego use el teorema de convergencia del punto fijo a éste método y explique el objetivo de su aplicación.