Los que construimos modelos econométricos de series temporales, generalmente encontramos situaciones en las que ciertos parámetros de dichos modelos (ARIMA), no son significativos y no debería estar en la ecuación final.
Eviews, por su facilidad y versatilidad en el manejo de modelos de series temporales, sin dudas es el referente de los econometristas de esta linea; sin embargo, R también hace un excelente trabajo con el paquete forecast, y permite estimar parámetros únicos silenciando o haciendo ceros a los demás.
¿Que es esto de silenciar parámetros?
En series temporales, sabemos que un proceso AR(2) viene definido como sigue:
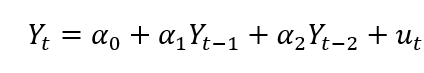
Pero muchas veces resulta por ejemplo que el primer rezago (Yt-1) no es significativo por lo que habría que quitarlo de la ecuación volver a probar, o probar con otras estructuras diferentes; todo dependerá de lo que diga la función de autocorrelación simple y parcial (y la paciencia de ir probando todas las posibles combinaciones).
Con este antecedente, este post intentará explicar cómo hacer cero, o silenciar un parámetro en específico y estimar sólo aquellos parámetros que son significativos. Los supuestos para realizar lo comentario anteriormente son:
- No se evaluará estacionariedad
- No se evaluará estacionalidad
- No se evaluará transformaciones
- No se evaluará otros procesos subyacentes (otros posibles modelos)
Considerando estas cuestiones solo para relajar el análisis, y haciendo mucho énfasis en que todas estas cosas deben de ser evaluadas al momento construir los modelos econométricos, procederemos a la explicación.
Para poder realizar paso a paso este post debes descargar la base de datos que utilizo y guardarla en alguna parte de tu computadora; las librerías que utilizaré son las siguientes:
library(forecast)
library(openxlsx)
library(ggplot2)
La primera es la que se utiliza para construir modelos ARIMA, la segunda para cargar bases de excel a RStudio y la tercera para utilizar la función autoplot, la cual gráfica automáticamente las funciones ACF y PACF mediante la librería ggplot y forecast.
Seteamos el directorio, cargamos la base y caracterizamos la data como una serie de tiempo que inicia en el año 2004, mes 1 y tiene una frecuencia mensual (12)
setwd("C:\\tudirectorio")
data <- read.xlsx("base.xlsx",detectDates = T)
tsdata <- ts(data, start=c(2004,1), frequency = 12)
La serie en estudio es el saldo en cartera comercial de una institución financiera del Ecuador y luce como sigue:
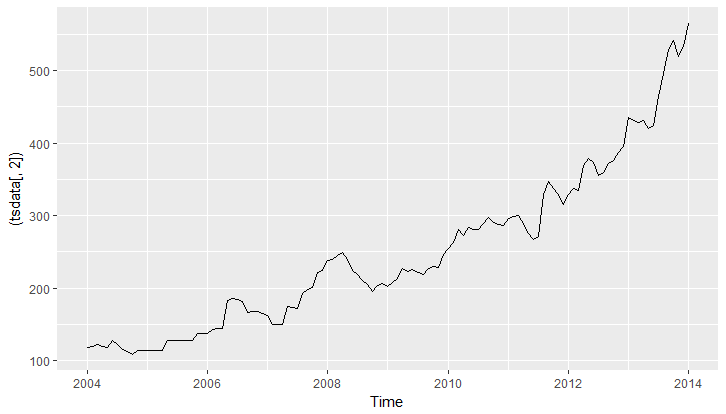
De la evolución de la serie podría sospecharse que no es estacionaria y por tanto se debe de diferenciar la serie. Insisto en esta parte se realicen los contrastes necesarios para llegar a dicha conclusión.
Veamos cómo luce la Función de autocorrelación simple y parcial usando la librería forecast con las funciones Acf y Pacf, y al librería ggplot2 con autoplot:
autoplot(Acf(diff(tsdata[,2],1),lag.max = 24))
autoplot(Pacf(diff(tsdata[,2],1),lag.max = 24))
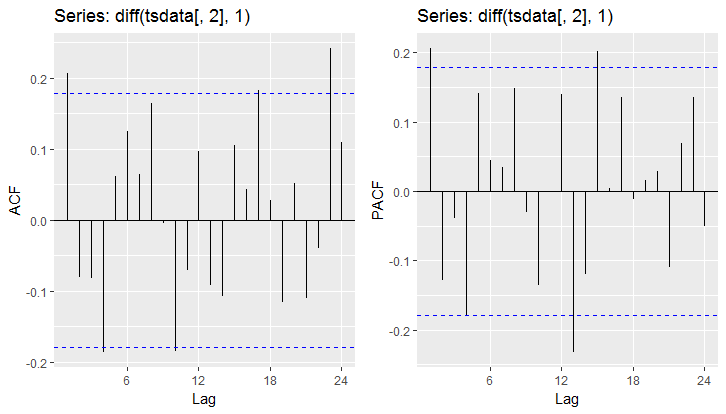
De la función de autocorrelación simple (ACF), se aprecia que podría tratarse de un modelo MA(1) MA(5), dado que las barras sobresalen de las lineas segmentadas de color azul; por otro lado, de la función de autocorrelación apreciar (PACF), podría tratarse solo de un AR(1).
Para probar el modelo ARIMA(1,1,5) donde, 1 que corresponde a un AR(1), 1 que corresponde a la primera diferencia ordinaria de la serie, 5 que corresponde a un MA(1) y MA(5), se procede como sigue:
modelo <- Arima(tsdata[,2],order=c(1,1,5),
fixed=c(NA,NA,0,0,0,NA))
summary(modelo)
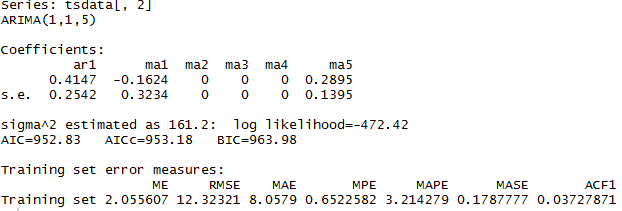
Se aprecia que los coeficientes ma2, ma3, ma4, son ceros (no son estimados, o son silenciados en la ecuación), por lo que solo nos interesa ma1 y ma5; haber incorporado todas las medias móviles podríamos incurrir en error de especificación.
Entre los comandos se encuentra la función fixed. Si contamos los parámetros a estimar en este pequeño modelo tenemos los siguientes: ar1, ma1,0,0,0,ma5; por lo tanto fixed=c(NA,NA,0,0,0,NA). Debido a que la serie está diferenciada, no estima el parámetro de la constante, por lo que no se muestra en la ecuación dicho parámetro. Si se hubiera incluido entonces se tendría que contar un NA al final de la función fixed.
Creo que con este ejemplo, se explica por sí misma la función fixed, dado que se aplica de la misma manera para los AR y cualquier orden.
Nótese que el proceso ma1 no es significativo, por lo que podríamos probar el modelo sin considerar dicho parámetro. Lo que tendríamos que hacer es manipular la función fixed como sigue:
modelo <- Arima(tsdata[,2],order=c(1,1,5),
fixed=c(NA,0,0,0,0,NA))
summary(modelo)
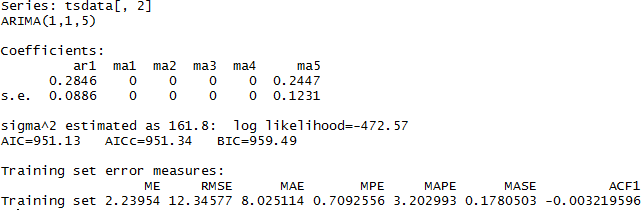
Donde los coeficientes estimados son significados al 95% de confianza (pruebe dividiendo 0.2846/0.0886, si la división es mayor que 2, entonces el coeficiente es estadísticamente significativo).
La forma de estimar con la función fixed es equivalente a escribir en Eviews:
d(comercial) ar(1) ma(5)


Salvo que forecast no devuelve el coeficiente sigmasq que denota la estimación de la varianza del error como un parámetro más dentro de la ecuación.
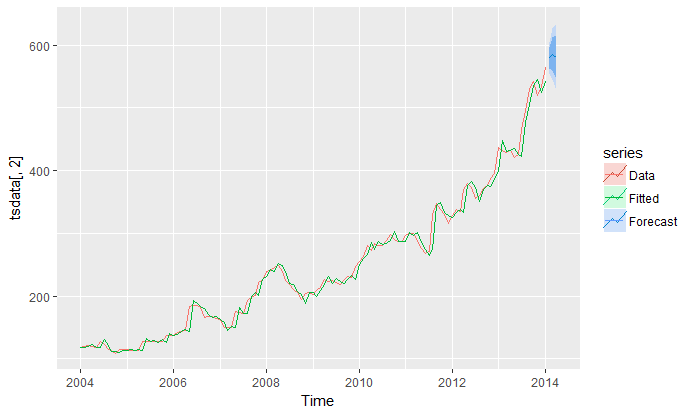
Finalmente, veamos cómo luce un pronóstico con este modelo para 3 datos fuera de la muestra:
proyeccion <- forecast(modelo,3)
autoplot(tsdata[,2], series="Data") +
autolayer(proyeccion, series="Forecast") +
autolayer(fitted(proyeccion), series="Fitted")
Extensión:
Para usuarios más avanzados, pueden generar un gráfico dinámico con la librería highcharter; resulta interesante poder seleccionar la serie o las proyecciones dentro del gráfico.
Puedes seguir mis publicaciones vía:
Nota: puedes solicitarme el script de RStudio para este ejemplo mediante cualquier de las vía de contacto anteriormente mencionadas o por correo.
Excelente trabajo, hace días atras hice esta pregunta que finalmente salgo de las dudas, gracias al trabajo suyo. Es evidente que el software EViews facilita este tipo de trabajo al igual que RATS, pero R por ser software libre es mas preferido. Saludos.
Muchas gracias por tu comentario Edwin. Me alegra haber podido aportar. Un abrazo.