Ejercicio: 1Eva_IT2009_T1 Suma de serie con signo alternado

mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]

Solicitar el número n, calcular cada término i-ésimos y acumularlos en una variable s.

1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}+\text{...}+\frac{1}{n}

El signo se puede alternar multiplicando una variable signo por -1. También se puede usar (-1)ⁱ⁺¹ para alternar el signo.

observe:

(-1)^{(1+1)}1+(-1)^{(2+1)}\frac{1}{2}+(-1)^{(3+1)}\frac{1}{3}+ ...

mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]

..

---

Algoritmo en Python: mientras-repita

La primera solución se presenta usando el lazo “Mientras-Repita”

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2009_T1 Suma de serie con signo alternado
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
n = int(input('¿Cuántos términos?: '))

# PROCEDIMIENTO
i = 1
s = 0
signo = 1
while (i<=n):
    s = s + signo*(1/i)
    i = i + 1
    signo = (-1)*signo

# SALIDA
print(s)

resultado del algoritmo

¿Cuántos términos?: 5
0.7833333333333332
>>> 
== RESTART: D:\MATG1052Ejemplos\unprograma.py ==
¿Cuántos términos?: 10
0.6456349206349207
>>> 

mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]
..

---

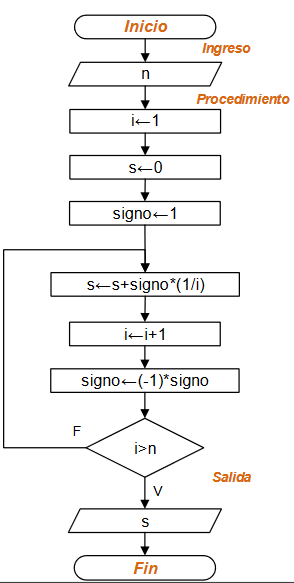
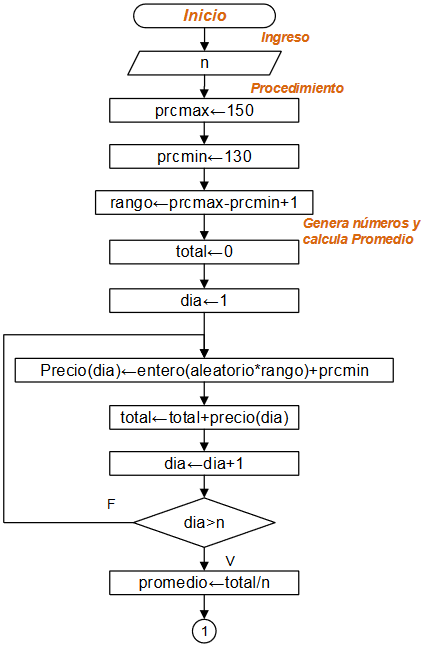
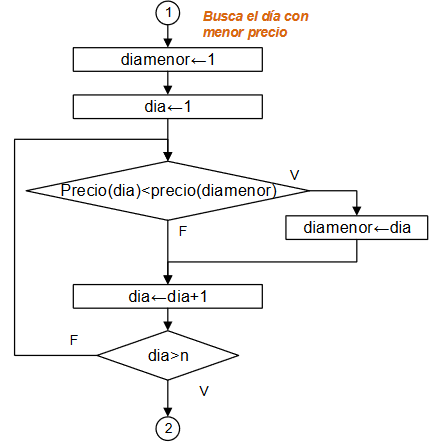
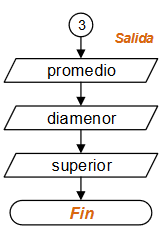
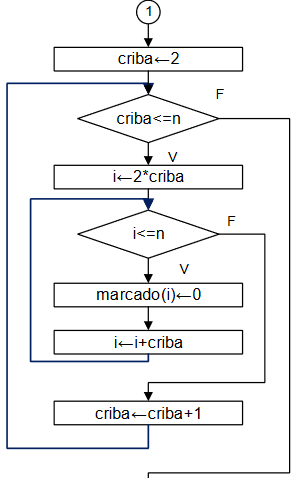
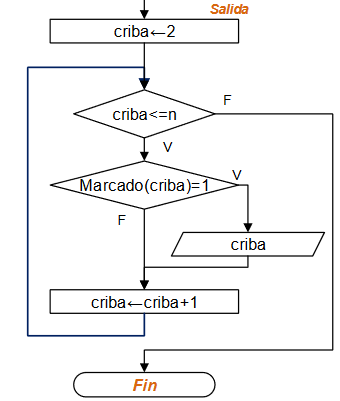
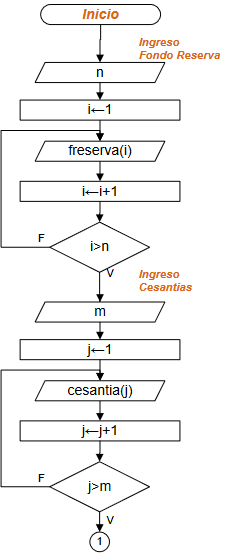
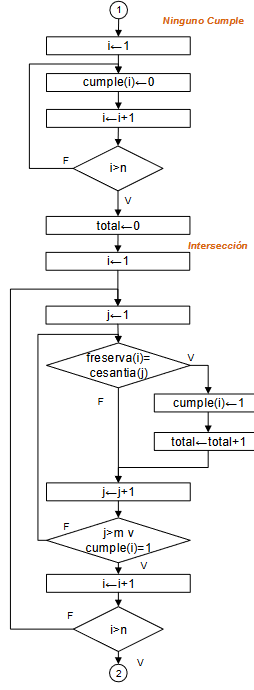
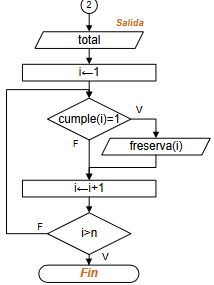
Diagrama de Flujo: Mientras-Repita

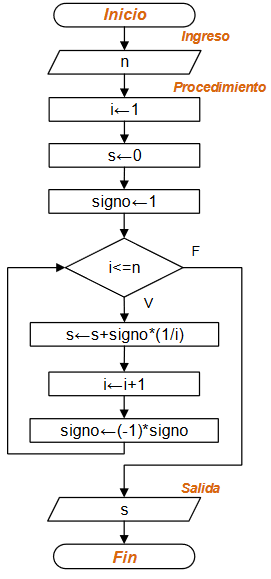
mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python: repita-hasta:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2009_T1 Suma de serie con signo alternado
# Propuesta de solución. edelros@espol.edu.ec

# INGRESO
n = int(input('¿Cuántos términos?: '))

# PROCEDIMIENTO
i = 1
s = 0
signo = 1
while not(i>n):
    s = s + signo*(1/i)
    i = i + 1
    signo = (-1)*signo

# SALIDA
print(s)

mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]
..

---

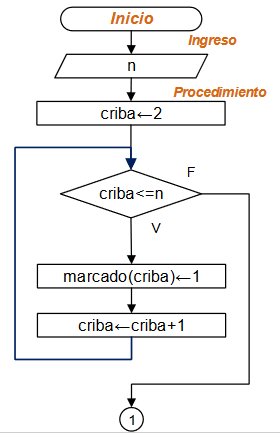
Diagrama de Flujo Repita-Hasta

mientras-repita: [ algoritmo ] [ diagrama flujo ]
repita-hasta: [ algoritmo ] [ diagrama flujo ]

---

Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab

ejercicios resueltos Python 1Eva_IT2009_T1 pdf

ejercicios resueltos Matlab 1eva_it2009_t1 pdf

Ejercicio: 1Eva_IIT2008_T1 Odómetro OCTAL

[ algoritmo ] [ diagrama flujo ]

Se usa el concepto para cambio de base numérica, se extrae cada dígito para acumular el valor ponderando por cada posición referenciada con la variable i.

Si se usa residuo de la división para 10, el primer dígito a extraer es el menos significativo (unidades).

    r = octal%10

Se acumulan los valores de acuerdo a la ponderación o peso por posición y se repite hasta que no queden dígitos que ponderar.

    octal = octal//10
    decimal = decimal+r*(8**i)

Para repasar: Bases Numéricas Introducción

Tarea: validar que el número es octal (rango de dígitos entre 0-7)

[ algoritmo ] [ diagrama flujo ]

..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2008_T1 Odometro OCTAL
# Propuesta de solución. edelros@espol.edu.ec
# Tarea: Validar que el ingreso sea en octal.

# INGRESO
octal = int(input('¿numero en octal?: '))

# PROCEDIMIENTO
i = 0
decimal = 0
while (octal>0):
    r = octal%10
    octal = octal//10
    decimal = decimal+r*(8**i)
    i = i + 1

# SALIDA
print('valor en decimal: ')
print(decimal)

Resultado del algoritmo

Observación: Tener en cuenta que no se ha validado que el número octal solo debe tener dígitos entre 0 y 7.

¿numero en octal?: 27
valor en decimal: 
23
>>> 
¿numero en octal?: 14
valor en decimal: 
12
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

---

Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab

ejercicios resueltos Python 1eva_iit2008_t1 pdf

ejercicios resueltos Matlab 1eva_iit2008_t1 pdf

Ejercicio: 1Eva_IT2008_T3 Simular Precio del Petróleo

[ algoritmo ] [algoritmo con vector ] [ diagrama flujo ]

Se ingresa la cantidad de días del mes,
o se puede considerar directamente 30.

También es opcional ingresar el rango de precio mínimo y precio máximo, que son los límites del número aleatorio.

Para la pregunta a) se calcula el promedio como el acumulado de precios de cada día dividido para los n días.

En la pregunta b) se usa el algoritmo del menor, con la hipótesis que el díamenor es el primero, y que el precio menor es el máximo posible, a fin que se reemplace con el primer menor encontrado.

Se deja la pregunta c) como tarea a fin de que se desarrolle el problema usando un arreglo.

[ algoritmo ] [algoritmo con vector ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T3 Simular Precio del Petróleo
# Propuesta: edelros@espol.edu.ec
# Tarea: Realizar el literal c)

import random as rnd

# INGRESO
n = int(input('días del mes: '))

# PROCEDIMIENTO
prcmax = 150
prcmin = 130
rango  = prcmax-prcmin+1
diamenor = 1
pmenor = prcmax

dia = 1
total = 0
while (dia<=n):
    precio = int(rnd.random()*rango)+prcmin
    total  = total+precio

    if (precio<pmenor):
        diamenor = dia
        pmenor   = precio

    dia = dia+1

promedio = total/n

# SALIDA
print('promedio: ')
print(promedio)
print('día de menor precio:')
print(diamenor)

[ algoritmo ] [algoritmo con vector ] [ diagrama flujo ]
..

---

Algoritmo en Python: usando arreglos

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T3 Simular Precio del Petróleo
# Tema 3. Precio petroleo-Arreglo
# Propuesta: edelros@espol.edu.ec

import random as rnd
import numpy as np

# INGRESO
n = int(input('días del mes: '))

# PROCEDIMIENTO
prcmax = 150
prcmin = 130
rango  = prcmax-prcmin+1
precio = np.zeros((n+1),dtype=int)

# algoritmo del promedio
total = 0
dia   = 1
while (dia<=n):
    precio[dia] = int(rnd.random()*rango)+prcmin
    total = total + precio[dia]
    dia   = dia + 1

promedio = total/n

# algoritmo del menor
diamenor = 1
dia = 1
while (dia<=n):
    if precio[dia]<precio[diamenor]:
        diamenor = dia
    dia = dia + 1

# algoritmo precio superior al promedio
superior = 0
dia = 1
while (dia<=n):
    if precio[dia]>promedio:
        superior = superior + 1
    dia = dia + 1

# SALIDA
print('promedio: ')
print(promedio)
print('día de menor precio:')
print(diamenor)
print('días con precio sobre promedio:')
print(superior)

Resultado del algoritmo

días del mes: 30
promedio: 
140.06666666666666
día de menor precio:
14
días con precio sobre promedio:
16
>>> 

[ algoritmo ] [algoritmo con vector ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [algoritmo con vector ] [ diagrama flujo ]

---

Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab

ejercicios resueltos Python 1eva_it2008_t3 pdf

ejercicios resueltos Python 1eva_it2008_t3_flujo pdf

ejercicios resueltos Matlab 1eva_it2008_t3 pdf

Ejercicio: 1Eva_IT2008_T2 Criba de Eratóstenes

[ algoritmo ] [ diagrama flujo ]

- Se forma un vector con todos los números naturales entre 2 y n.

i	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
criba[i]	1	1	0	1	0	1	0	0	0	1	0	1	0	0	0	1	0	1	0

Llenar un arreglo de marcas o tachado con la hipótesis que todos son primos(1).

# PROCEDIMIENTO
marcado = np.zeros((n+1),dtype=int)
# hipotesis: todos son primos
criba = 2
while (criba<=n):
    marcado[criba] = 1
    criba = criba+1

La prueba de hipótesis consiste en usar un indicador para el número de criba, y otro indicador i para anular marcando con cero (0) las posiciones de los múltiplos.

- Se tachan todos los múltiplos de 2 que son menores que n,

Inicie eliminando los múltiplos de 2, para luego cambiar a los múltiplos de 3, etc.

# no son primos los múltiplos 
criba = 2
while (criba<=n):

    # revisa el primer múltiplo
    i = criba * 2
    while (i<=n):
        marcado[i] = 0
        i = i + criba
    criba = criba+1

Mostrar como resultado solo aquellos números mantienen en marcas válidas (1).

Tarea: Analizar si es necesario hacer funcionar el algoritmo de la prueba de hipótesis hasta n o un número menor. Realizar la validación que n sea mayor que 1.

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T2 Criba de Eratóstenes
# Propuesta: edelros@espol.edu.ec

import numpy as np

# INGRESO
n = int(input('primos menores que: '))

# PROCEDIMIENTO
marcado = np.zeros((n+1),dtype=int)

# hipotesis: todos son primos
criba = 2
while (criba<=n):
    marcado[criba] = 1
    criba = criba+1

# no son primos los múltiplos 
criba = 2
while (criba<=n):

    # revisa el primer múltiplo
    i = criba * 2
    while (i<=n):
        marcado[i] = 0
        i = i + criba
    criba = criba+1

# SALIDA
criba = 2
while (criba<=n):
    if marcado[criba]==1:
        print(criba)
    criba = criba+1

resultado del algoritmo

primos menores que: 30
2
3
5
7
11
13
17
19
23
29
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

---

Otra forma de plantear el algoritmo

# 1ra Evaluación I Término 2008
# Tema 2. Criba de Eratóstenes
import numpy as np

# INGRESO
n = int(input('cuantos numeros analiza: '))

# PROCEDIMIENTO
# vector de números naturales
natural = np.zeros(n, dtype=int)
posicion =  0
while not(posicion>=n):
    natural[posicion] = posicion
    posicion = posicion +1

# hipotesis todos cumplen
cumple = np.ones(n,dtype = int)

# Tarea: analiza cada posición
posicion = 2
# elimina multiplos / no cumplen
contador = 2
tacha  = posicion *contador
while not(tacha>(n-1)):
    tacha  = posicion *contador
    if tacha<(n-1):
        cumple[tacha] = 0
    contador = contador +1

# SALIDA
# solo valores de la posicion 2 en adelante
print(natural[2:])
print(cumple[2:])

mostrando el siguiente resultado:

cuantos numeros analiza: 50
[ 2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19
 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
 38 39 40 41 42 43 44 45 46 47 48 49]
[1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1]
>>> 

[ algoritmo ] [ diagrama flujo ]

---

Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab

ejercicios resueltos Python 1eva_it2008_t2 pdf

ejercicios resueltos Matlab 1eva_it2008_t2 pdf

Ejercicio:  1Eva_IT2008_T1 Teorema de Wilson

“Un número p es primo si y solo si el factorial (p-1)! + 1 es divisible por p”.

El ejercicio se divide en dos partes principales:
- determinar si un número es primo
- Si es primo, validar lo que indica Wilson

Para la primera parte, se usa el concepto de residuo de la división para determinar si el número es primo.

# revisa esprimo 
esprimo = 1
divisor = 2
while not(divisor>=n or esprimo==0):
    r = n%divisor
    if (r == 0):
        esprimo = 0
    divisor = divisor + 1

La bandera usada es "esprimo" que inicia con el supuesto de ser verdadero ó 1.

Solo si el número resulta ser primo, se aplican las operaciones de Wilson. Primero determinando el valor del factorial,

wilson = -1
if esprimo == 1:
    
    # factorial
    factor = 1
    i = 1
    while not(i>=n):
        factor = factor*i
        i = i + 1

y luego revisar Wilson

    # revisa Wilson 
    residuo = (factor + 1) % n
    if residuo == 0:
        wilson = 1
    else:
        wilson = 0

Se añaden los bloques de ingreso y salida para completar el algoritmo

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IT2008_T1 Teorema de Wilson

# INGRESO
n = int(input('ingrese numero primo: '))
while not(n>0):
    n = int(input('ingrese numero positivo: '))

# PROCEDIMIENTO

# revisa esprimo 
esprimo = 1
divisor = 2
while not(divisor>=n or esprimo==0):
    r = n%divisor
    if (r == 0):
        esprimo = 0
    divisor = divisor + 1

wilson = -1
if esprimo == 1:
    
    # factorial
    factor = 1
    i = 1
    while not(i>=n):
        factor = factor*i
        i = i + 1
    
    # revisa Wilson 
    residuo = (factor + 1) % n
    if residuo == 0:
        wilson = 1
    else:
        wilson = 0

# SALIDA
print('cumple Wilson: ', wilson)

resultado del algoritmo

ingrese numero primo: 7
cumple Wilson:  1
>>> 
== RESTART: D:\Ejemplos\unprograma.py ==
ingrese numero primo: 13
cumple Wilson:  1
>>> 
== RESTART: D:\Ejemplos\unprograma.py ==
ingrese numero primo: 8
cumple Wilson:  -1
>>> 

Ejercicio: 1Eva_IIT2007_T3 Garantías de prestamos IESS

[ algoritmo ] [ diagrama flujo ]

Para el ejemplo, por simplicidad se usan cédulas de 3 dígitos; también se supone que no existen elementos repetidos dentro de cada arreglo.

i reserva(i) 1 987 2 876 3 765 4 654 ... ... n

j cesantia(j) 1 876 2 765 3 .. m

En la nota se indica que las listas de las cédulas de los afiliados tienen tamaño diferente, además el ingreso de datos es separado por tener origen de datos diferentes.

# INGRESO

# datos de afiliados con fondo de reserva
n = int(input('Afiliados con Fondo de Reserva: '))
freserva = np.zeros(n+1,dtype=int)
i = 1
while not(i>n):
    print(i)
    freserva[i] = input('ingrese cedula:')
    i = i + 1

Al inicio del algoritmo, se supondrá que ningún afiliado cumple con los requisitos, por lo que se usa un arreglo de banderas de cumple o no cumple  (1 ó 0).

# Hipotesis: Ninguno cumple requisito
cumple = np.zeros(n+1,dtype=int)

Realizar una búsqueda ordenada de números de cédula:
- para cada cédula de reserva[i] con n elementos
- realizar una búsqueda en el arreglo de cesantía[j] para los m elementos.

# Revisa listado buscando iguales
total = 0
i = 1
while not(i>n):
    j = 1
    while not(j>m or cumple[i]==1):
        if freserva[i]==cesantia[j]:
            cumple[i] = 1
            total = total + 1
        j = j + 1
    i = i + 1

Repetir el proceso, marcando el arreglo de banderas, cumple, cada vez que se encuentra un valor repetido entre ambas listas.

Tarea: Realizar el ejercicio, construyendo un tercer arreglo con solamente los elementos que cumplen con la condición.

[ algoritmo ] [ diagrama flujo ]
..

---

Algoritmo en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2007_T3 Garantías de prestamos IESS
# propuesta: edelros@espol.edu.ec

import numpy as np

# INGRESO

# datos de afiliados con fondo de reserva
n = int(input('Afiliados con Fondo de Reserva: '))
freserva = np.zeros(n+1,dtype=int)
i = 1
while not(i>n):
    print(i)
    freserva[i] = input('ingrese cedula:')
    i = i + 1

# datos de afiliados con cesantía
m = int(input('Afiliados con Cesantia: '))
cesantia = np.zeros(m+1,dtype=int)
j = 1
while not(j>m):
    print(j)
    cesantia[j] = input('ingrese cedula:')
    j = j + 1

# PROCEDIMIENTO

# Hipotesis: Ninguno cumple requisito
cumple = np.zeros(n+1,dtype=int)

# Revisa listado buscando iguales
total = 0
i = 1
while not(i>n):
    j = 1
    while not(j>m or cumple[i]==1):
        if freserva[i]==cesantia[j]:
            cumple[i] = 1
            total = total + 1
        j = j + 1
    i = i + 1

# SALIDA: Muestra cedulas de los que cumplen requisito
print('Cumplen requisitos:')
print(total)
print('listado: ')
i = 1
while not(i>n):
    if (cumple[i]==1):
        print(freserva[i])
    i = i + 1

ejemplo de resultado del algoritmo

Afiliados con Fondo de Reserva: 3
1
ingrese cedula:123
2
ingrese cedula:234
3
ingrese cedula:345
Afiliados con Cesantia: 2
1
ingrese cedula:123
2
ingrese cedula:345
Cumplen requisitos:
2
listado: 
123
345
>>> 

[ algoritmo ] [ diagrama flujo ]
..

---

Diagrama de Flujo

[ algoritmo ] [ diagrama flujo ]

---

Propuesta de solución con diagrama de flujo, Python y otra versión con Matlab

ejercicios resueltos Python 1eva_iit2007_t3 pdf

ejercicios resueltos Matlab 1eva_iit2007_t3 pdf