Autor: Edison Del Rosario

Ejercicio: 1Eva_IIT2003_T2 Sumar términos de progresión geométrica

Propuesta de solución con diagrama de flujo y Python: python en pdf .
Otra versión con matlab en pdf

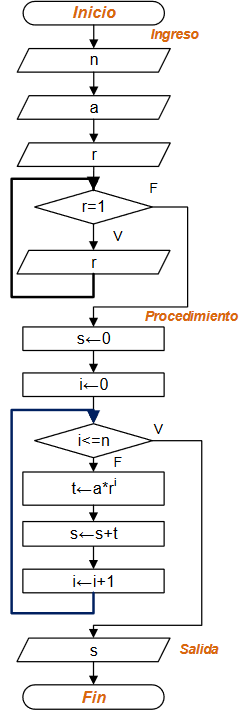
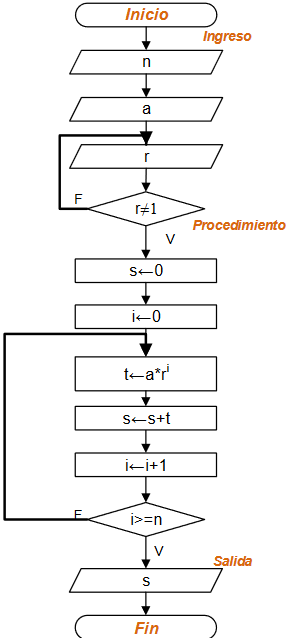
Ingresar la cantidad n de términos, el factor a y r, validando que r no sea 1.

S = \sum_{i=0}^{n} a + ar + ar^2 + ar^3 + ... + ar^n

Iniciar con 0 las variables: s que acumula términos, i como el contador de términos que adicionalmente se usa como exponente.

# PROCEDIMIENTO
s = 0
i = 0
while (i<=n):
    t = a*(r**i)
    s = s + t
    i = i + 1

Como paso siguiente, calcular cada término y acumularlos en s tantas veces como sea necesario hasta que que i llega a n.

El resultado buscado se encontrará en s.

Observe que el primer término es solo la constante a, con equivalente ar⁰.

Lazo mientras-repita:

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2003_T2 Sumar términos de progresión geométrica
# Propuesta de solución. edelros@espol.edu.ec.

# INGRESO
n = int(input('¿Valor de n?: '))
a = float(input('factor a: '))
r = float(input('factor r: '))
while (r==1):
    r = int(input('factor r debe ser diferente de 1: '))

# PROCEDIMIENTO
s = 0
i = 0
while (i<=n):
    t = a*(r**i)
    s = s + t
    i = i + 1

# SALIDA
print(s)

Diagrama de Flujo

ejercicios resueltos Python parc_iit2003_t2 pdf

ejercicios resueltos Matlab parc_iit2003_t2 pdf

Ejercicio: 1Eva_IIT2003_T1 Cambiar Decimal a Octal

Propuesta de solución en Python

Empiece con los conceptos expuestos en el tema de Bases Numéricas Introducción, el ejercicio es una aplicación del tema.

Propuesta con elementos principales, quedan partes por desarrollar:

• validar octal de 4 dígitos
• validar en procedimiento,
• que los dígitos sean octales [0,7]

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 1Eva_IIT2003_T1 Cambiar Decimal a Octal
# propuesta: edelros@espol.edu.ec

#INGRESO
octal = int(input('número octal: '))

# PROCEDIMIENTO
decimal = 0
i = 0
while (octal>0):
    digito  = octal%10 # residuo
    octal   = octal//10 # cociente
    decimal = decimal + digito*(8**i)
    i = i+1

# SALIDA
print('número en decimal: ', decimal)

Ejercicio:  2Eva_IT2003_T4 Registro de carros en archivo

Propuesta de solución en Python:

Se ingresan los datos de los carros en una lista, añadiendo los datos con la instrucción append().

Para el literal a, se concatenan los datos de una fila añadiendo una coma ‘,’ como separador. se escribe cada línea en el archivo.

En el literal b, se recorre la lista analizando los datos de los carros para añadirlos en una lista aparte que contiene los datos de los seleccionados.

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IT2003_T4 Registro de carros en archivo
# Tarea: validar datos de ingreso

# INGRESO
n = int(input('cuantos carros: '))
tabla = []
i = 0
while (i<n):
    print('Datos del carro: ... ',i)
    placa = input('Placa: ')
    anio  = input('año: ')
    tipo  = input('tipo A/auto C/camioneta: ')
    marca = input('marca: ')
    color = input('color: ')
    precio = input('precio: ' )

    registro = [placa,anio,tipo,marca,color,precio]
    tabla.append(registro)
    i = i+1

# PROCEDIMIENTO
# literal a)
nombre  = 'carros.dat'
archivo = open(nombre,'w')
i = 0
while (i<n):
    linea = ''
    j = 0
    while (j<6):
        linea = linea + tabla[i][j] + ','
        j = j + 1
    linea = linea.strip(',')+'\n'
    archivo.write(linea)
    i = i + 1
    
archivo.close()

# literal b
selecciona = []
i = 0
while (i<n):
    if (int(tabla[i][1])>1995 and tabla[i][4]=='rojo' and int(tabla[i][5])<6000):
        selecciona.append(tabla[i][0])
    i = i + 1

# SALIDA
print('archivo guardado')
print(' los autos que cumplen el pedido son:')
print(selecciona)

Ejercicio: 2Eva_IT2003_T1 Funciones promedio, mayor y menor

Propuesta de solución en Python: py_pdf, también versión en matlab: m_pdf

Se requiere desarrollar las funciones usando las operaciones para mostrar el conocimiento de los conceptos.

Como los datos se envían en un vector, se debe recorrer cada elemento del vector para obtener los resultados. Esta parte muestra su dominio del manejo de lazos/bucles con los índices de un arreglo.

Instrucciones en Python

# ICM00794-Fundamentos de Computación - FCNM-ESPOL
# 2Eva_IT2003_T1 Funciones promedio, mayor y menor
# Se EVALUA escribir un algoritmo
# Evite usar las funciones del lenguaje de programación
# Propuesta de Solución: edelros@espol.edu.ec

def promedio(vector):
    n = len(vector)
    suma = 0
    for i in range(0,n,1):
        suma = suma + vector[i]
    prm = suma/n
    return (prm)

def mayor(vector):
    n = len(vector)
    # Busca cual es el mayor
    max = 1
    for i in range(0,n,1):
        if (vector[i]>vector[max]):
            max = i
    # presenta el valor de mayor
    z = vector[max]
    return (z)

def menor(vector):
    n = len(vector)
    # Busca cual es el menor
    min = 1
    for i in range(0,n,1):
        if (vector[i]<vector[min]):
            min = i
    # presenta el valor de menor
    z = vector[min]
    return (z)


# PROGRAMA de prueba de funciones
import numpy as np

# INGRESO
meses = 12
temperatura = np.zeros(meses,dtype=int)
for mes in range(0,meses,1):
    temperatura[mes] = int(input("temperatura["+str(mes+1)+"]: "))

# PROCEDIMIENTO
tprom = promedio(temperatura)
tmax  = mayor(temperatura)
tmin  = menor(temperatura)
diferencia = tmax-tmin

# SALIDA
print("promedio: "+str(tprom))
print("Diferencia max-min: "+str(diferencia))

resultado del algoritmo

temperatura[1]: 30
temperatura[2]: 32
temperatura[3]: 30
temperatura[4]: 28
temperatura[5]: 29
temperatura[6]: 25
temperatura[7]: 25
temperatura[8]: 23
temperatura[9]: 25
temperatura[10]: 27
temperatura[11]: 29
temperatura[12]: 30
promedio: 27.75
Diferencia max-min: 9

ejercicios resueltos Python final_it2003_t1 pdf

ejercicios resueltos Matlab final_it2003_t1 pdf